这里分别从平面2D 和 空间3D来说明。

平面上的包络线

In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. 为了方便理解，这里以下图为例进行说明：

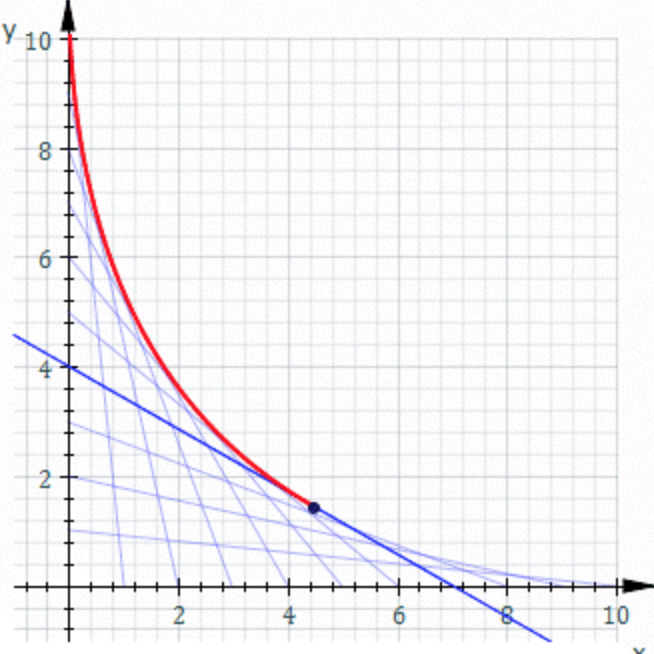
一个棍子靠墙不断移动，整个过程是个离散过程，无限密集时，则棍子每相邻的两个状态时候相交于一个点，这个点的连续运动轨迹就是这族曲线的包络。 这里，曲线是这族直线的包络，具体有以下几个特点：

• 平面上的包络是一条曲线；
• 相邻两条直线的交点在曲线（包络）上，该点称为Characteristic point(特征点)；
• 特征点的轨迹是包络；
• 直线与包络线在特征点处相切。

求平面上曲线族的包络线的方法

设曲线族关于参数t满足的方程 F(t,x,y)=0，求解方程组

\[\begin{cases} F(t,x,y) = 0 \\ F_t(t,x,y) = 0 \end{cases}\]

消去变量t得到的方程G(x,y)=0就是包络线。

空间上的包络面

推广到空间，则一族曲面的包络面为曲面。特殊地，当曲面变成平面时，一族平面的包络面为可展曲面。

• 空间上的包络是一个曲面；
• 相邻两个平面的交线是Characteristic curve(特征线)；
• 特征线即直母线rulings，轨迹是可展曲面；
• 平面与可展曲面在特征线处相切。

求空间中曲面族的包络面的方法

设曲面族关于参数t满足的方程 F(t,x,y,z)=0，求解方程组

\[\begin{cases} F(t,x,y,z) = 0 \\ F'_{t}(t,x,y,z) = 0 \\ F''_{tt}(t,x,y,z) = 0 \end{cases}\]

消去变量t得到的方程G(x,y,z)=0就是包络面。这个过程不易得到，如果由上式推导得出

\[\begin{cases} x = x(t) \\ y = y(t) \\ z = z(t) \end{cases}\]

则c(x,y,z) = c(x(t), y(t), z(t))称为regression curve.

• F 交 F't = rulings = Characteristic curve；
• F 交 F't 交 F''tt = c = regression curve；
• c’ // rulings；
• 可展曲面 S(t,u) = c(t) + u * c'(t).