直纹面Ruled surface

直纹面：一族直线连续运动扫过的曲面，直线称为rulings (直母线)或者generators.

直纹面的参数方程是 X(u,v) = a(u) + v r(u).

每个相对固定的u，对应的v r(u) 为直母线.

直纹面的分类

当det(a'(u), r(u), r'(u)) = 0，对于一条直母线ruling上的每个点的切平面都相同，这样的ruling称为 torsal ruling. 反之，称为non-torsal.

每条ruling都是torsal tuling的直纹面，就是可展曲面.

直纹面可以用(n,1)次Bezier张量积曲面表示.

而non-torsal ruling的直纹面中，特殊地，当n=1时，就是双曲抛物面hyperbolic paraboloid.

可展曲面Developable surface

按照上面的定义，当每一条直母线上每一点处的切平面都相同时，这样的直纹面就是可展曲面.

• 可展曲面是torsal直纹面，det(a'(u), r(u), r'(u)) = 0.
• 可展曲面可等距变换成平面.
• 可展曲面变换过程具有内蕴几何不变量，保角，保弧长，具有相同的第一基本形式.
• 可展曲面高斯曲率为0.
• 可展曲面上只有平点flat point和抛物点parabolic point.
• Surface of constant slope(常坡度的曲面)是可展曲面.
• 任意曲面的主法曲率线上的曲面法向量构成可展曲面.

可展曲面的分类

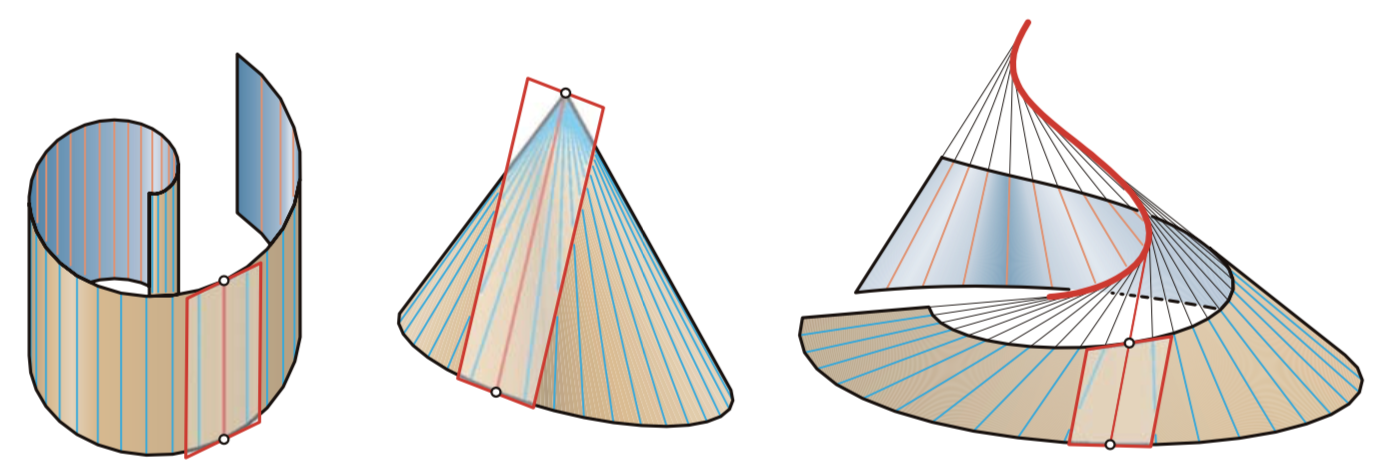
可展曲面只分为三类基本形式，即柱面，锥面，切曲面，其他可展曲面为这三类的组合形式.

1. cylindrical surface s(u,v)=l(u) + v r, r非零.
2. conical surface s(u,v)=v r(u), r非零.
3. tangent surface s(u,v)=c(u) + v c'(u)