给定torus曲面 \(x(u,v)=((a+rcos u)cos v, (a+rcosu)sinv, rsinu), (u,v)\in [0, 2\pi]\times [0, 2\pi]\) $a>r>0$, 计算沿着曲面上曲线$c(u(t), v(t))$的切可展面:
- $(u(t), v(t))= (\frac{\pi}{4}, t)$;
- $(u(t), v(t))= (t, 0)$;
- $(u(t), v(t))= (t, t)$;
- 展示可展切平面的直母线,即沿着曲线$c$的共轭切向量。
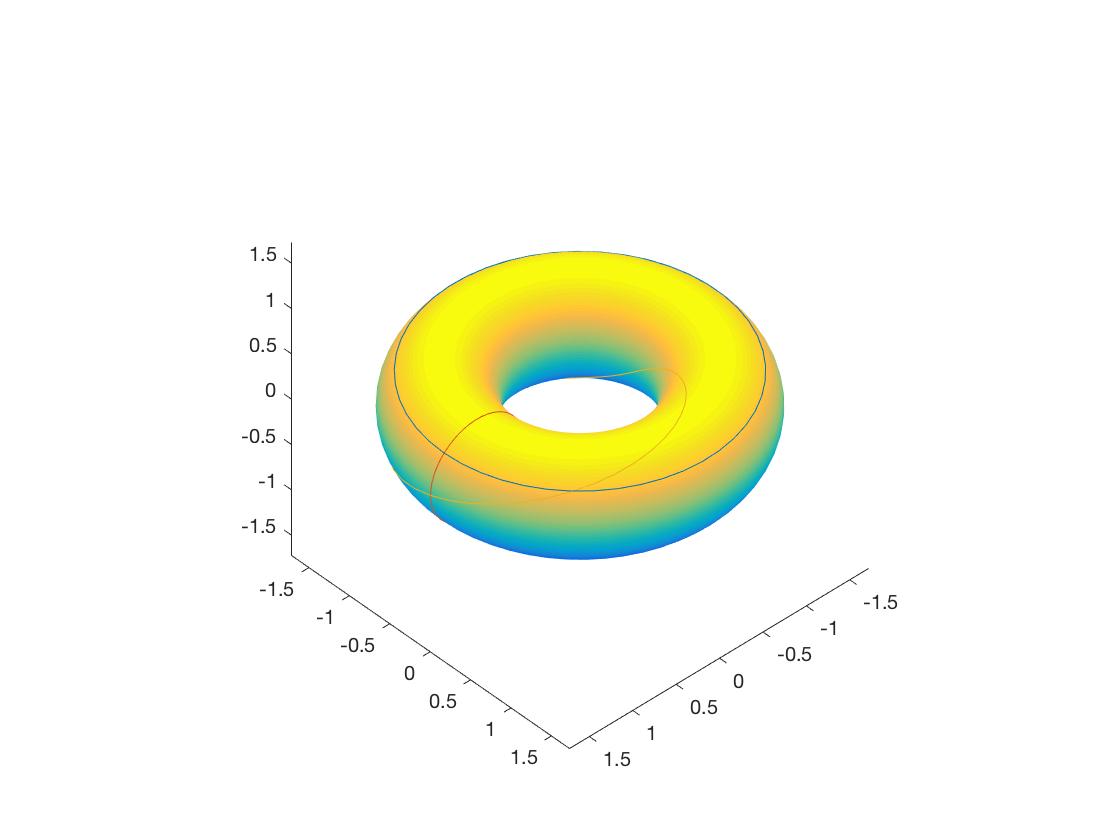
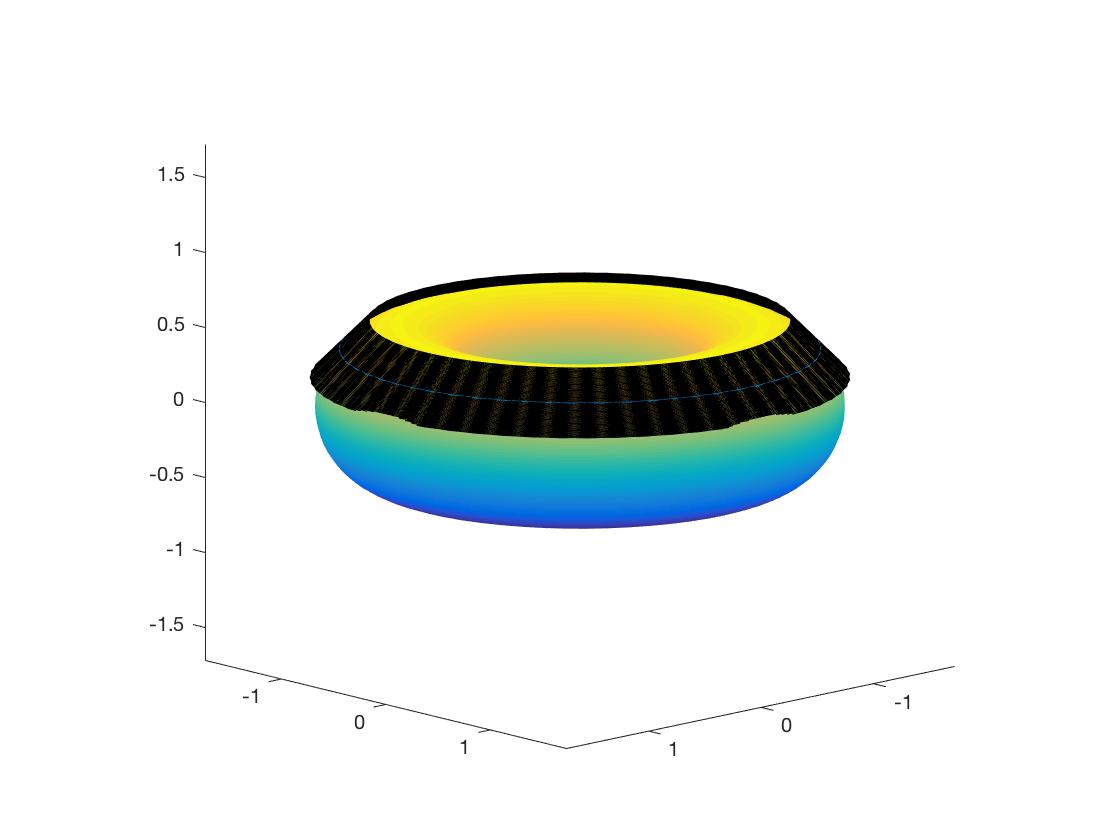
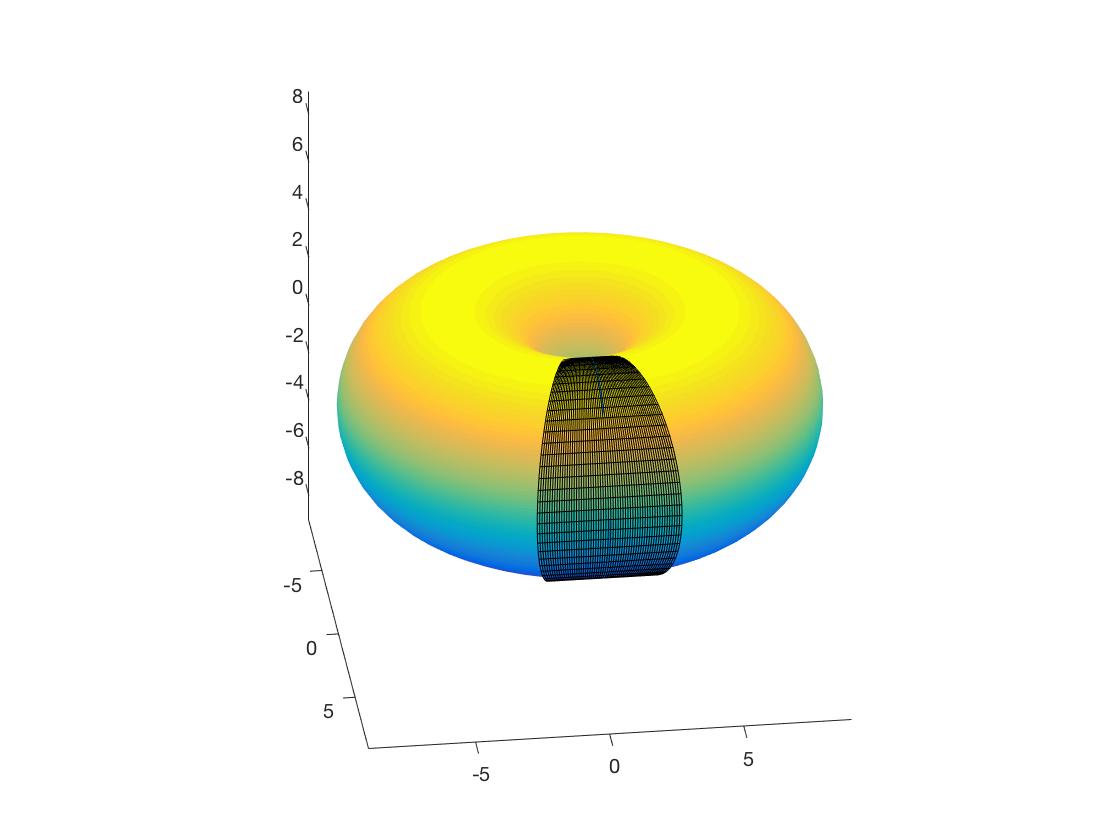
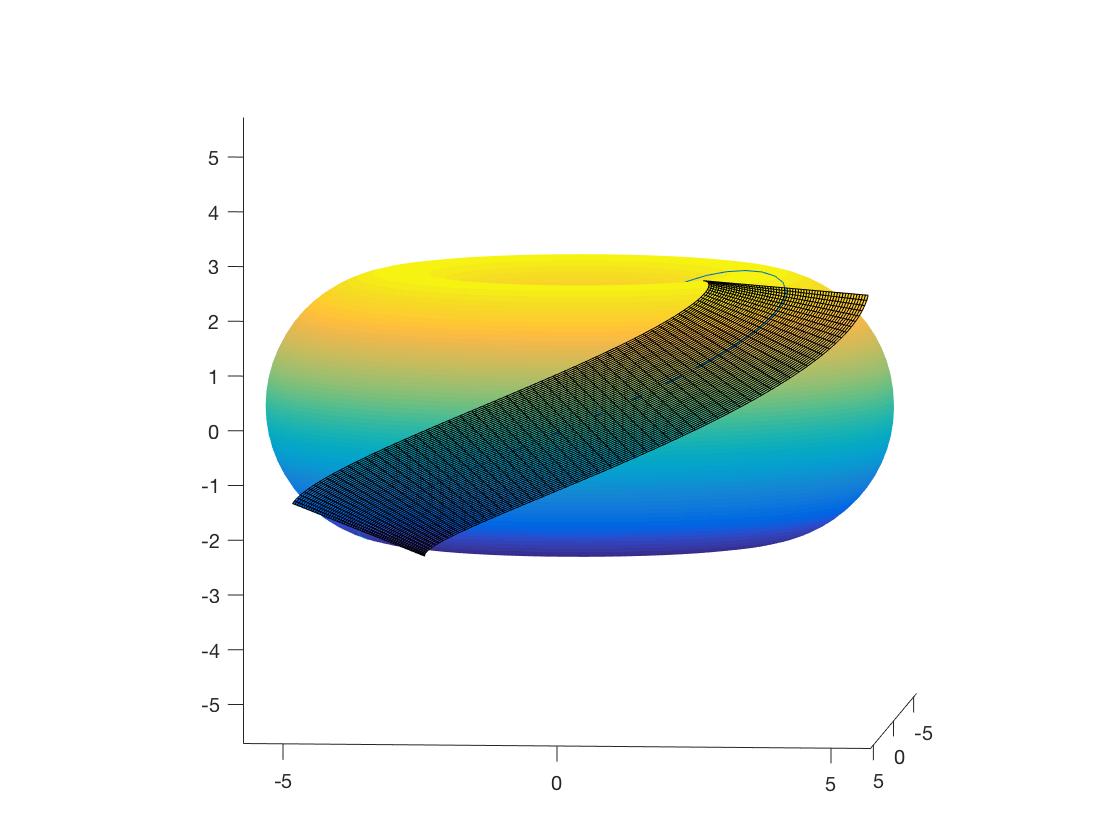
给定torus曲面 \(x(u,v)=((a+rcos u)cos v, (a+rcosu)sinv, rsinu), (u,v)\in [0, 2\pi]\times [0, 2\pi]\) $a>r>0$, 计算沿着曲面上曲线$c(u(t), v(t))$的切可展面:



