Offsets

From the geometric point of view, a surface has no thickness. However, in architecture one often builds with shells. Thus, we need to give our surface model a certain thickness to make it more realistic. 几何角度曲面没有厚度，为了实现出来，需要增加厚度，则需要考虑等距面。

Offsets curves 等距线

• An offset has the same curve normals as the original curve, and thus the corresponding tangents of c and cd in corresponding points are parallel.
• Offset curves are sometimes referred to as parallel curves.
• Offsets can be obtained as envelopes of circles with radius d centered at the curve c.

Computing offset curves.

• c(t) = (x(t), y(t)),
• n(t)= (−y'(t),x'(t))/ (x'(t)^2 + y'(t)^2)^{1/2},
• c_d(t) = c(t) ± d⋅n(t).

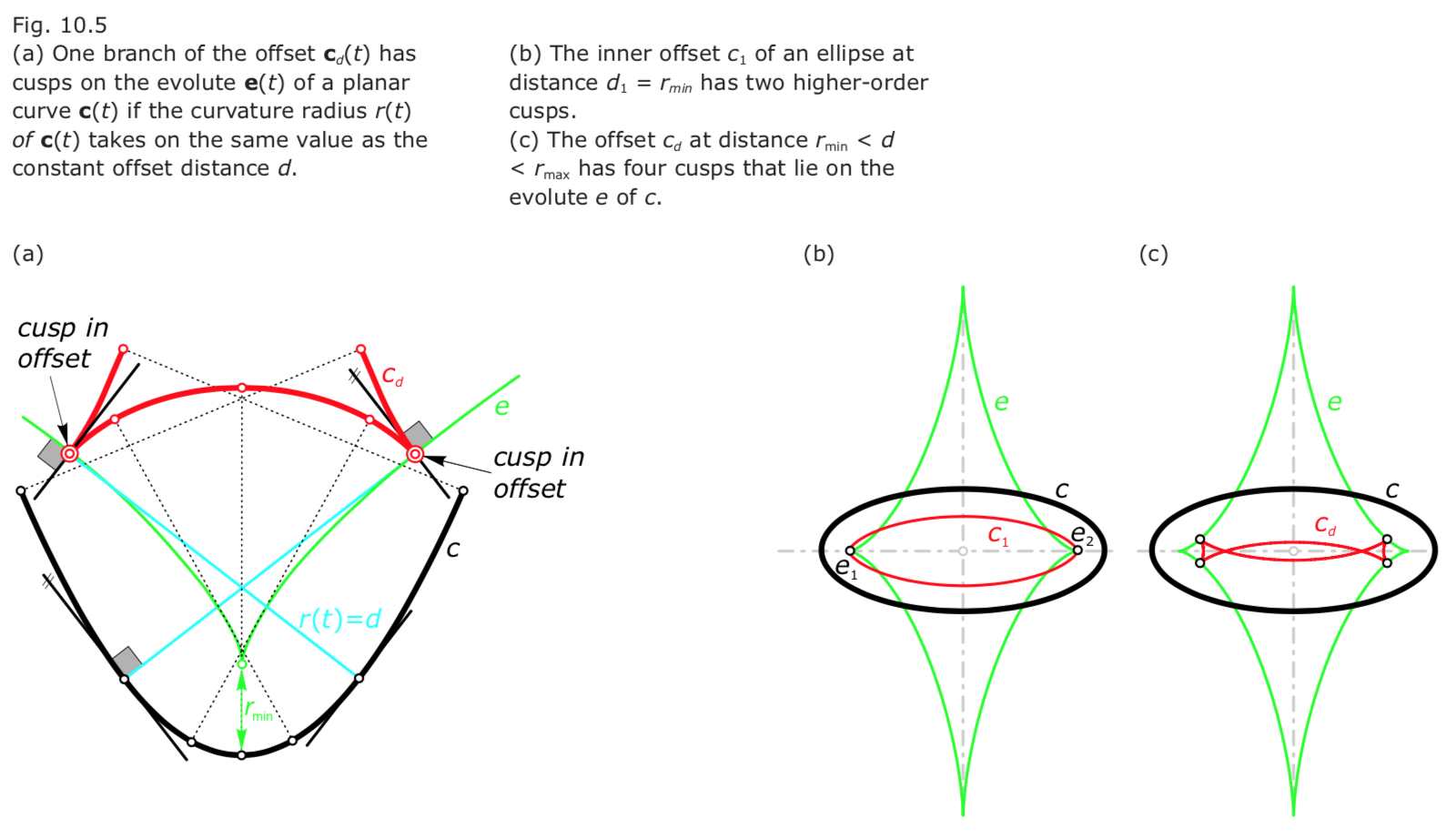
Curve, offset, and evolute.

• The normals of $c$ and $c_d$ are the tangents of the evolute $e$.
• At a cusp, the offset curve meets the evolute orthogonally.

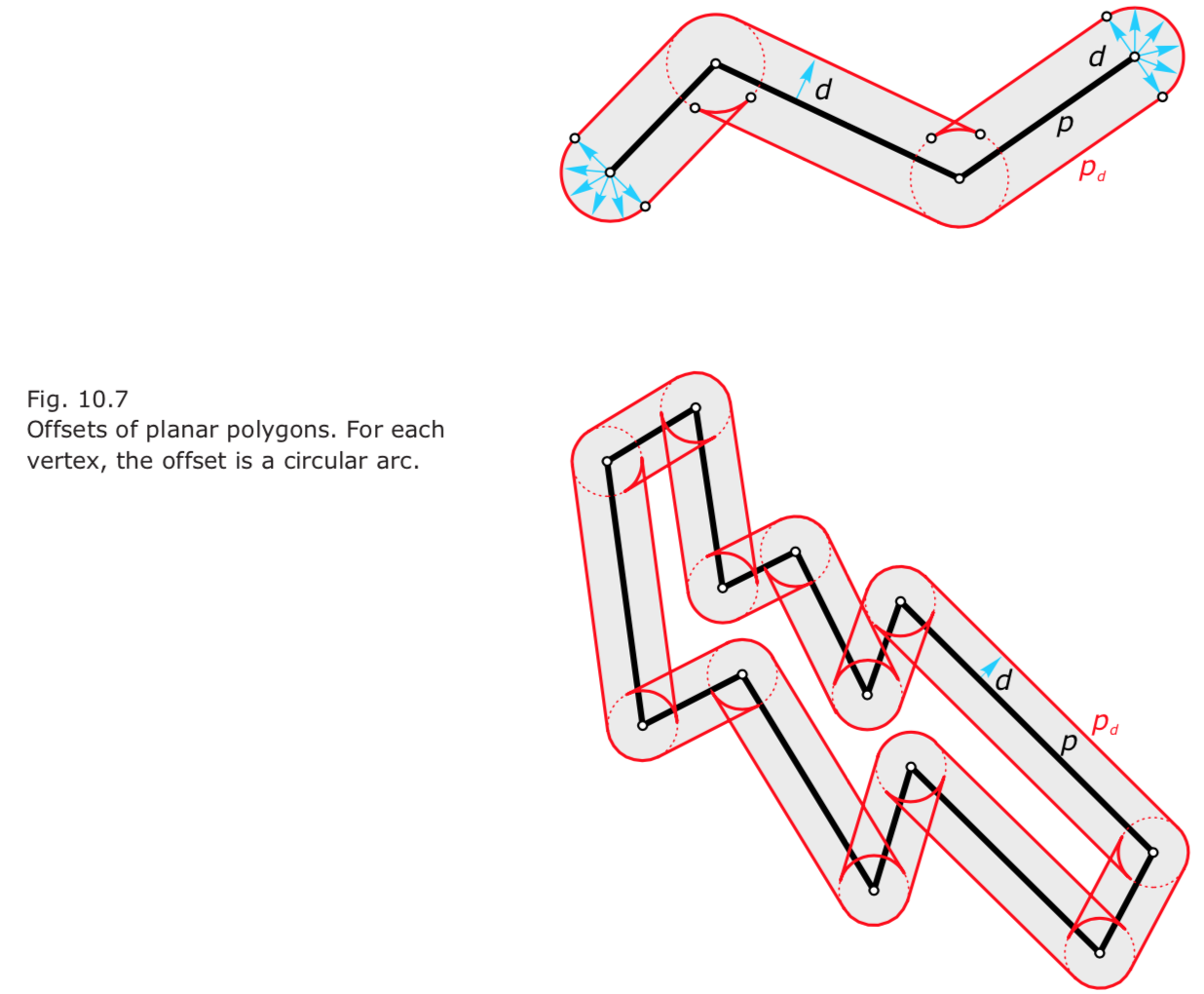
Offsets of planar polygons.

• Thus, one branch of the offset $p_d$ at constant distance $d$ consists of line segments (corresponding to the edges of p) and circular arcs (corresponding to the vertices of $p$).

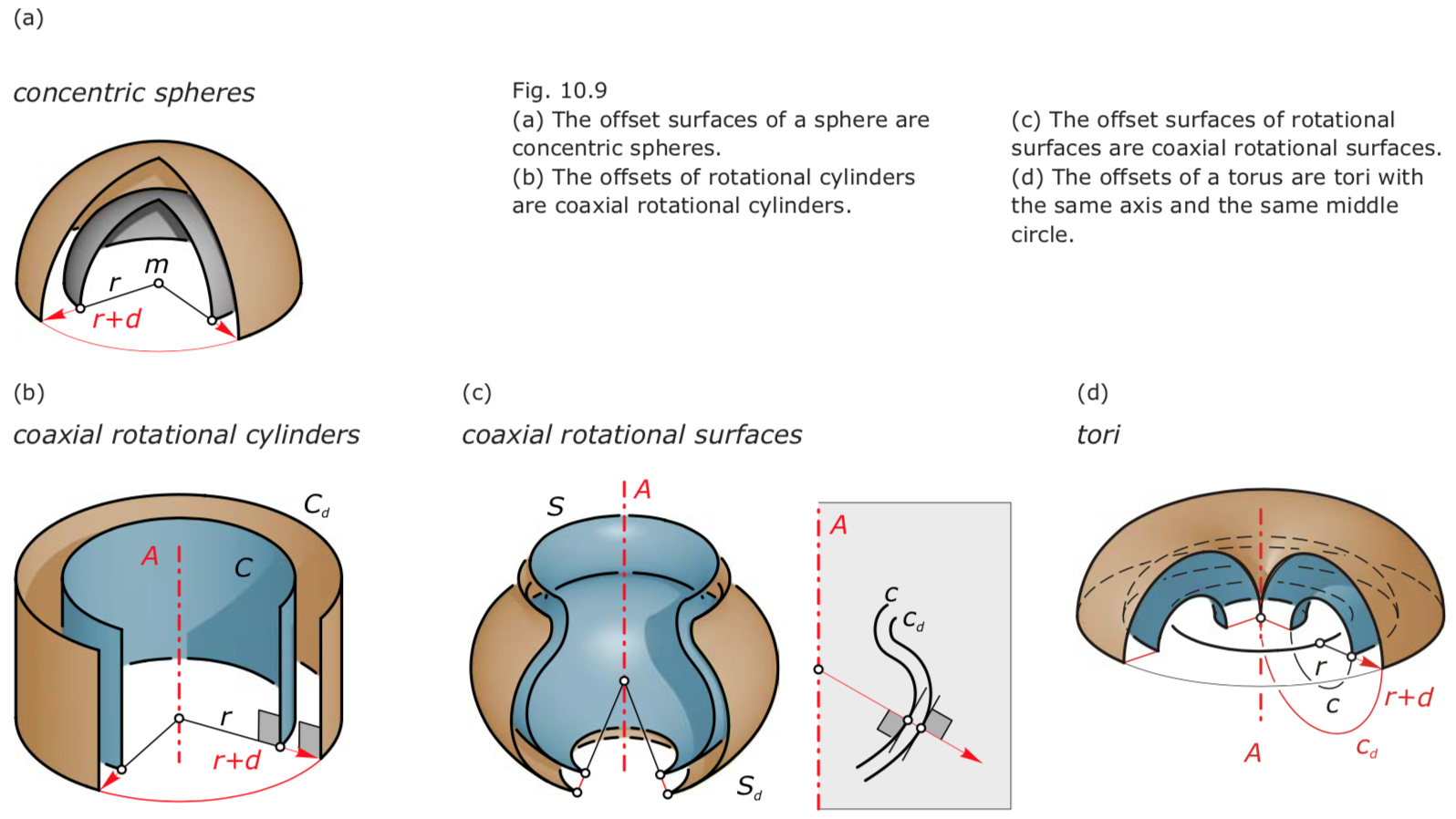
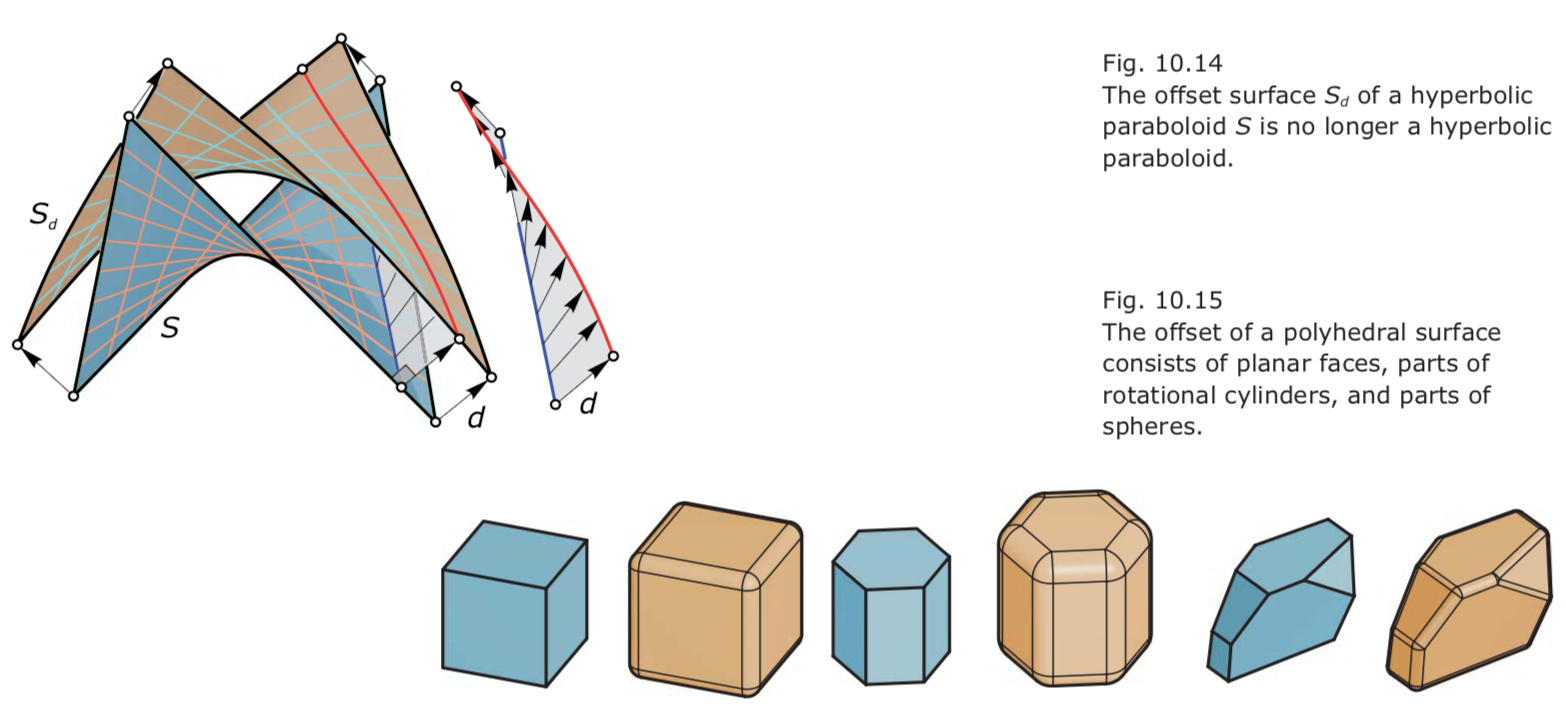
Offsets surfaces 等距面

• S(u,v) = (x(u,v), y(u,v), z(u,v))
• S_d(u,v) = S(u,v) ± d · n(u,v).
• Only special surface classes have the property that their offsets are again of the same surface type. These include cylinders and rotational surfaces.
• The offsets of the sphere are again spheres, and thus the offsets of a torus are again tori with the same axis and the same middle circle.

Offsets of polyhedral surfaces.

• The offset surface $S_d$ of a hyperbolic paraboloid S is no longer a hyperbolic paraboloid.

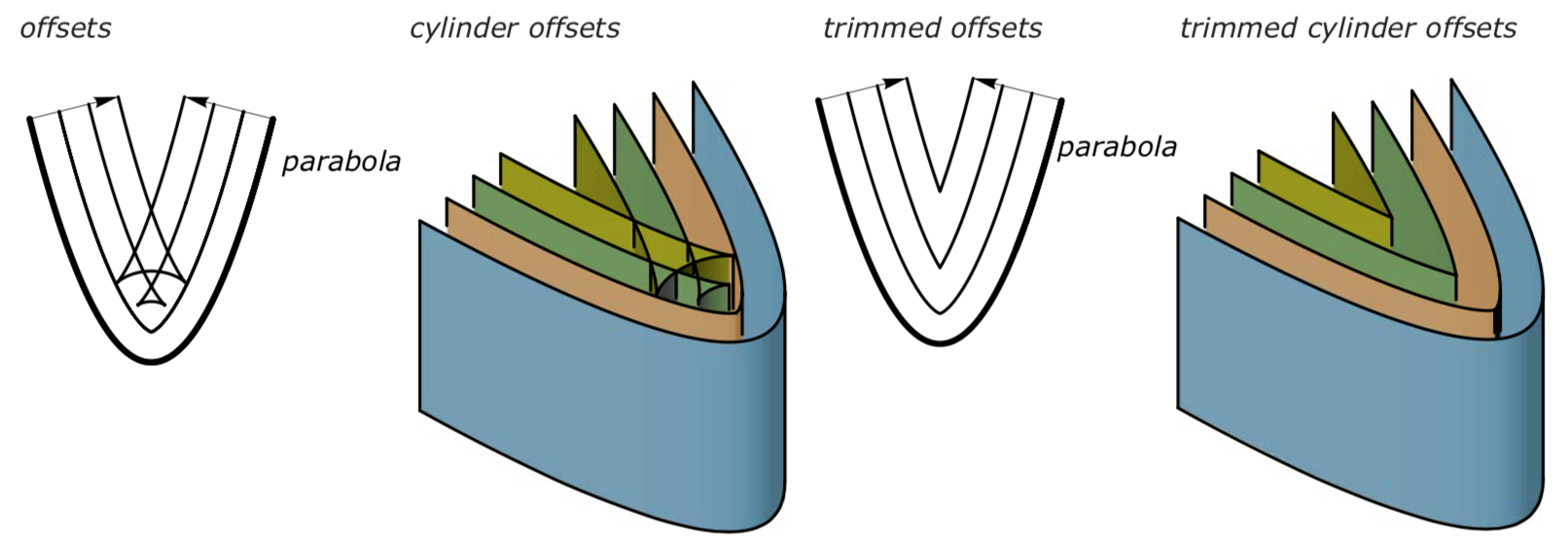
Trimming of offsets 修剪等距

• Thus, for practical applications one sometimes needs to remove these parts of the offset curve.
• By local trimming we remove parts of the offset that overlap because the offset curve intersects the evolute of the original curve.
• Global trimming is necessary to remove parts of the initial offset curve that overlap but result from distinct regions of the original curve.

Application of offsets 等距应用

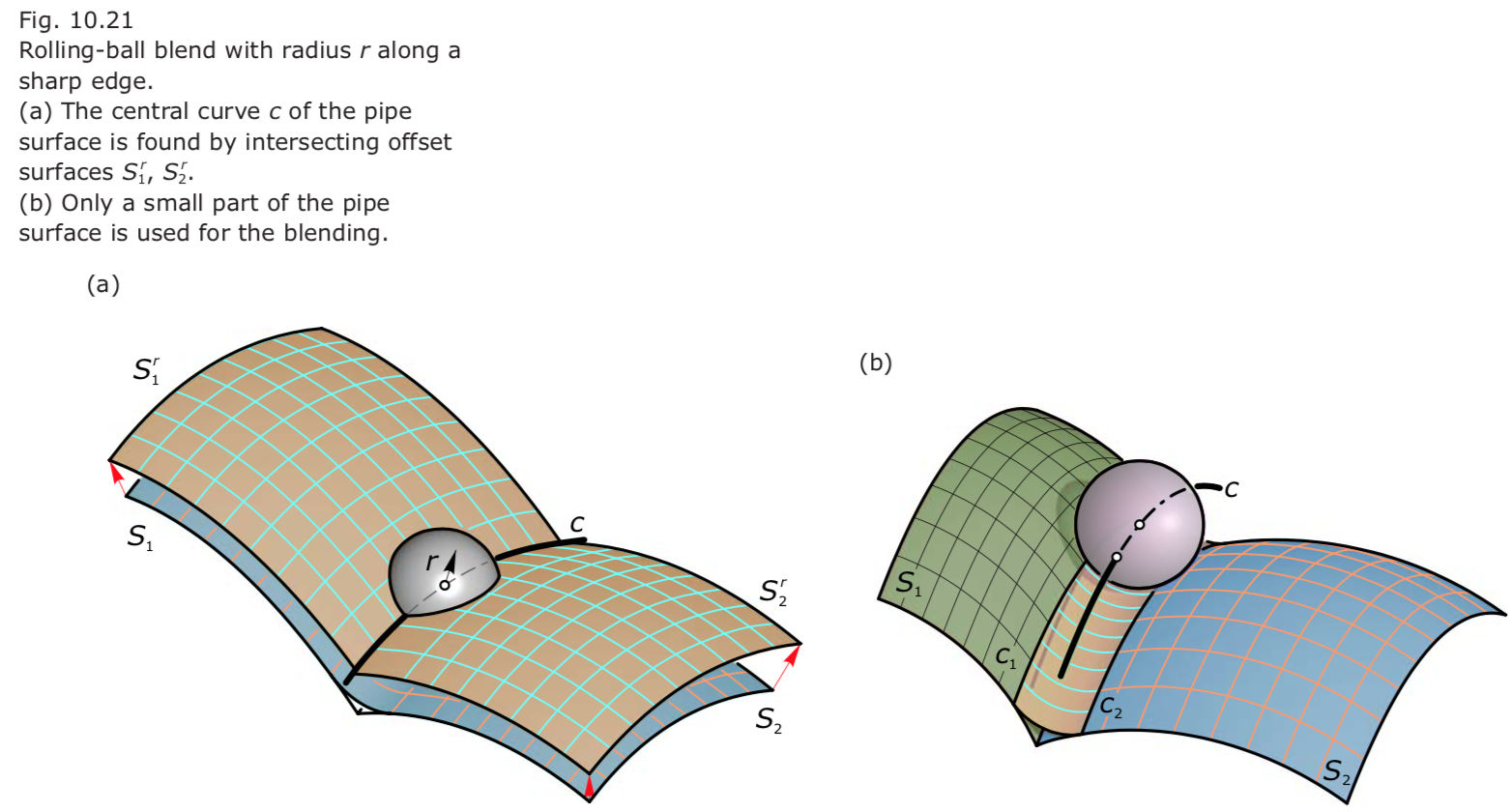
Rolling ball blends

• Such a pipe surface is generated by rolling a ball of radius $r$ “along the edge” such that it always touches both surfaces.

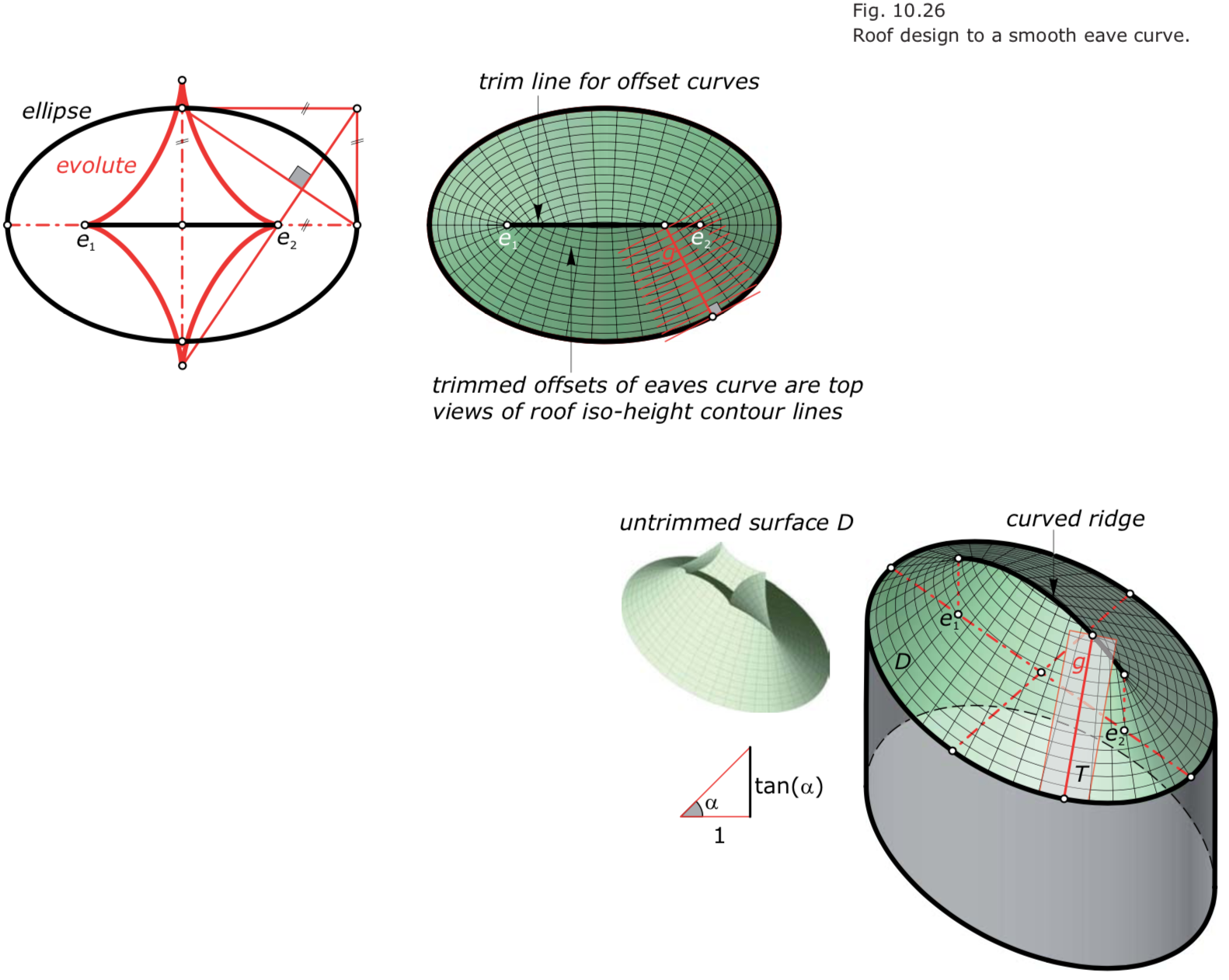
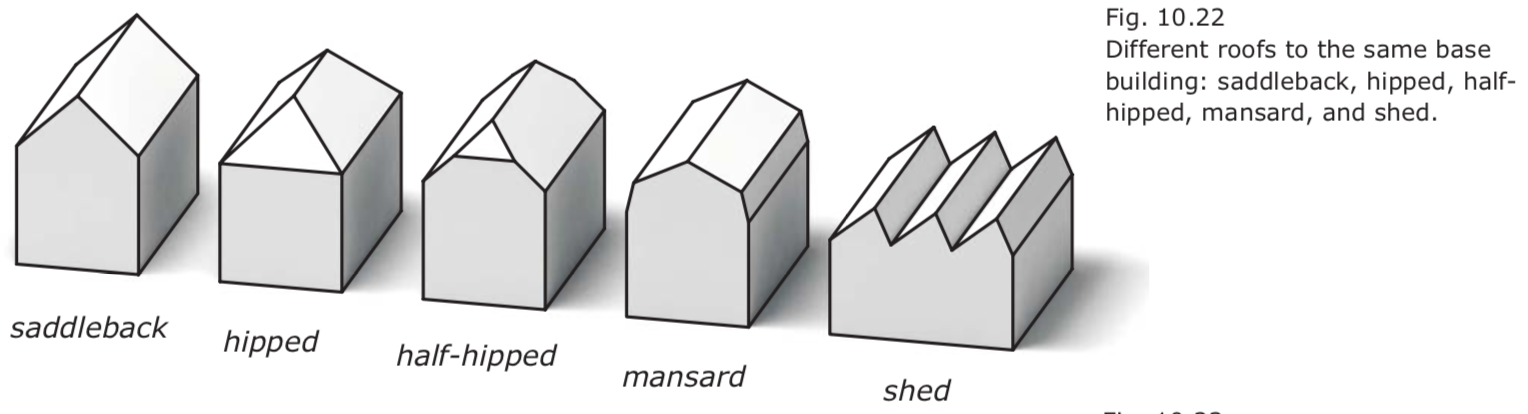
Designing roofs using Offsets

• The geometric shape of a roof is driven by a combination of drainage constraints, the floor plan, and stylistic considerations.

• The main idea is that the offset polygons of the eave polygon (formed by the eaves) are nothing more than the top views of the iso-height contour lines of the roof.

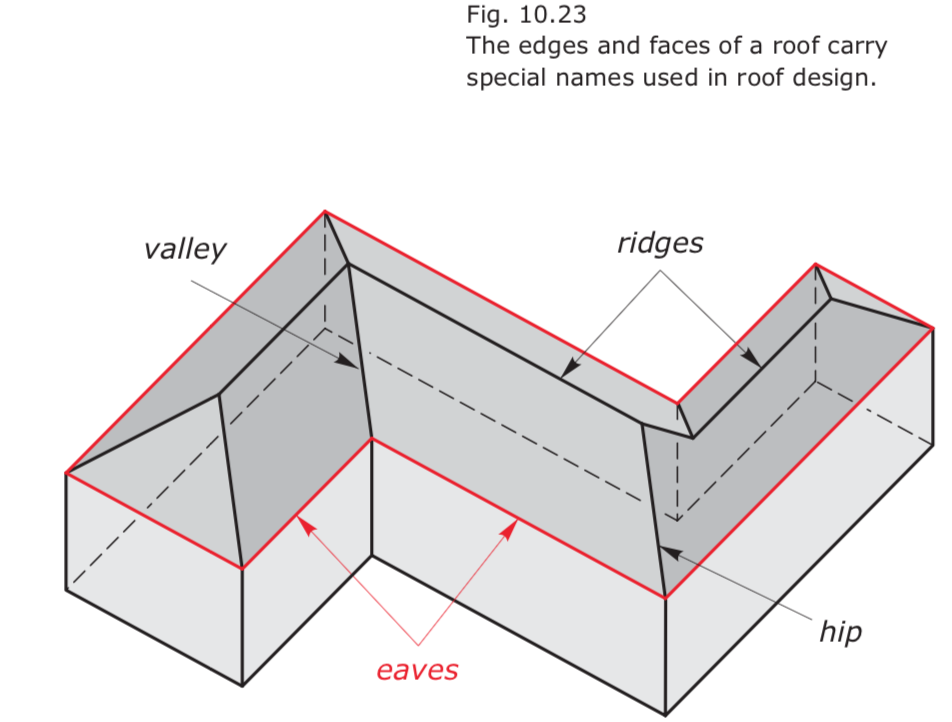
• Using offsets, we find the top views of hips, valleys, and ridges of the roof as follows.

• We can also design roofs of constant slope to smooth eave curves. Then the roof will be formed by a developable surface of constant slope.