Polyhedra and polyhedral surfaces

• both bounded by planar faces
• polyhedron 多面体 由 平面面+直线+格点 组成
• polyhedral surface 多面体曲面 由 平面面组成，不一定构成立体，可以存在边界点、边

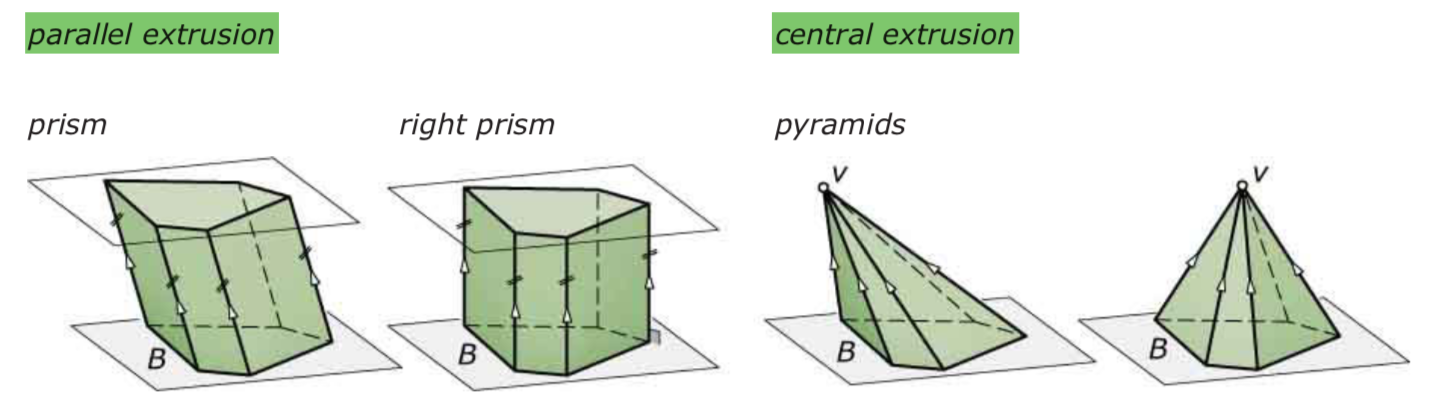
Pyramids and prisms 棱锥和棱柱

• pyramids 棱锥：底为多边形，侧面为三角形
• prisms 棱柱：底和顶通过平移得到，特殊为直棱柱(right prisms)
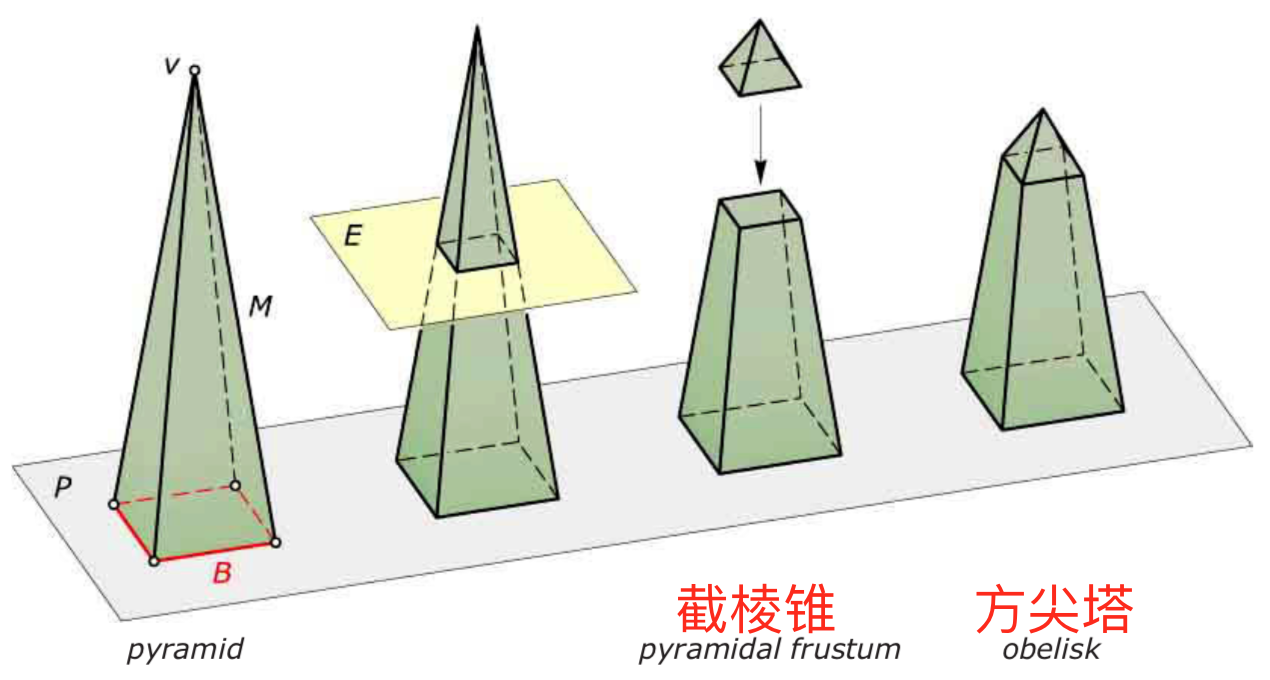
• obelisk 方尖塔：由截棱锥(pyramidal frustum)组成

Platonic solids 柏拉图固体

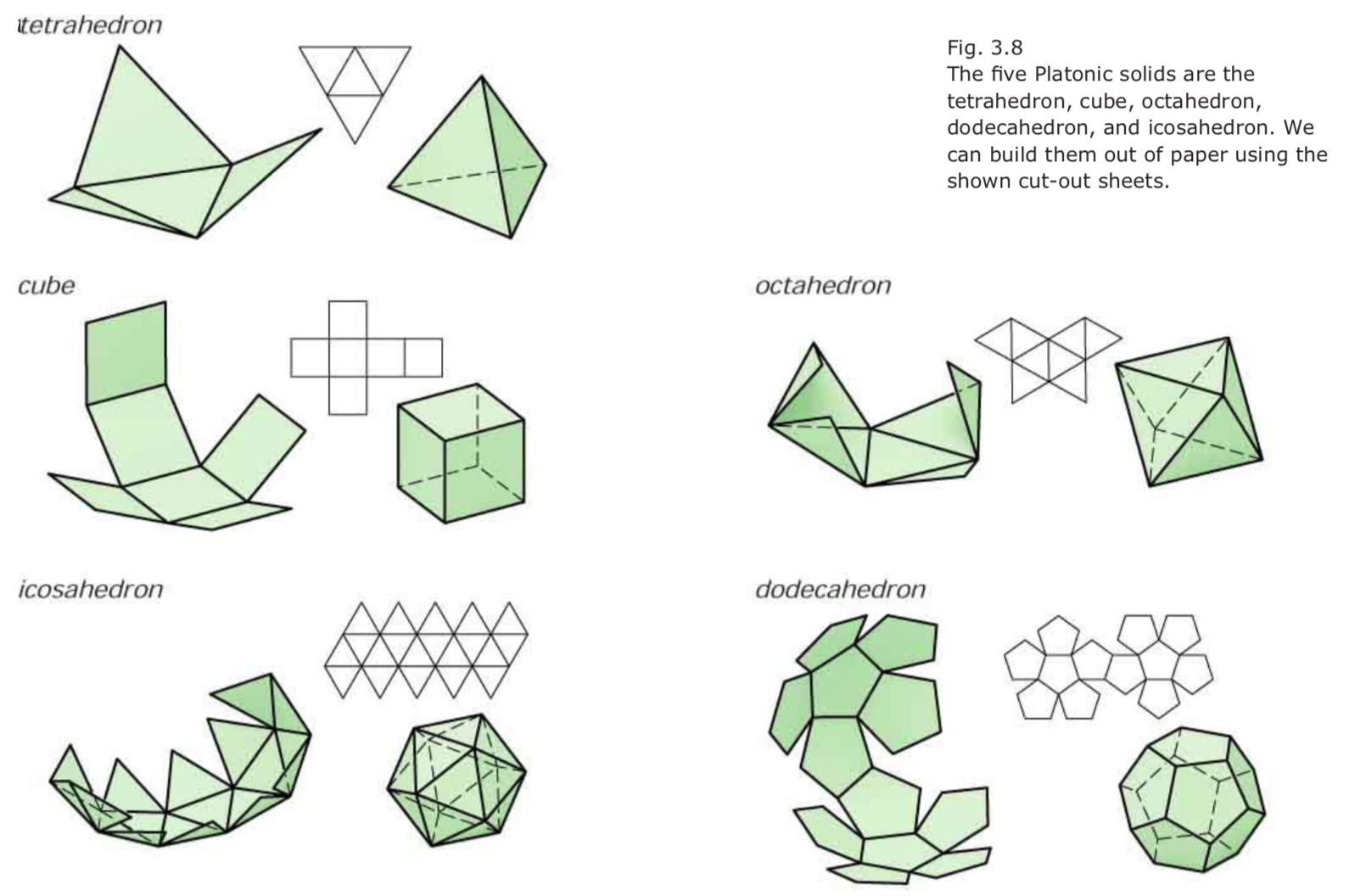
• 柏拉图固体：每个面为全等的正则多边形，每个格点处有相同面数
• 只有5种：tetrahedron四面体, hexahedron=cube六面体, octahedron八面体, docecahedron十二面体, icosahedron二十面体
• 凸多面体：连续边角和< 360°
• 4D空间：6个多面体满足Platonic solids
• 5D及以上空间：3个满足，分别是hyercube, simplex, cross polytope
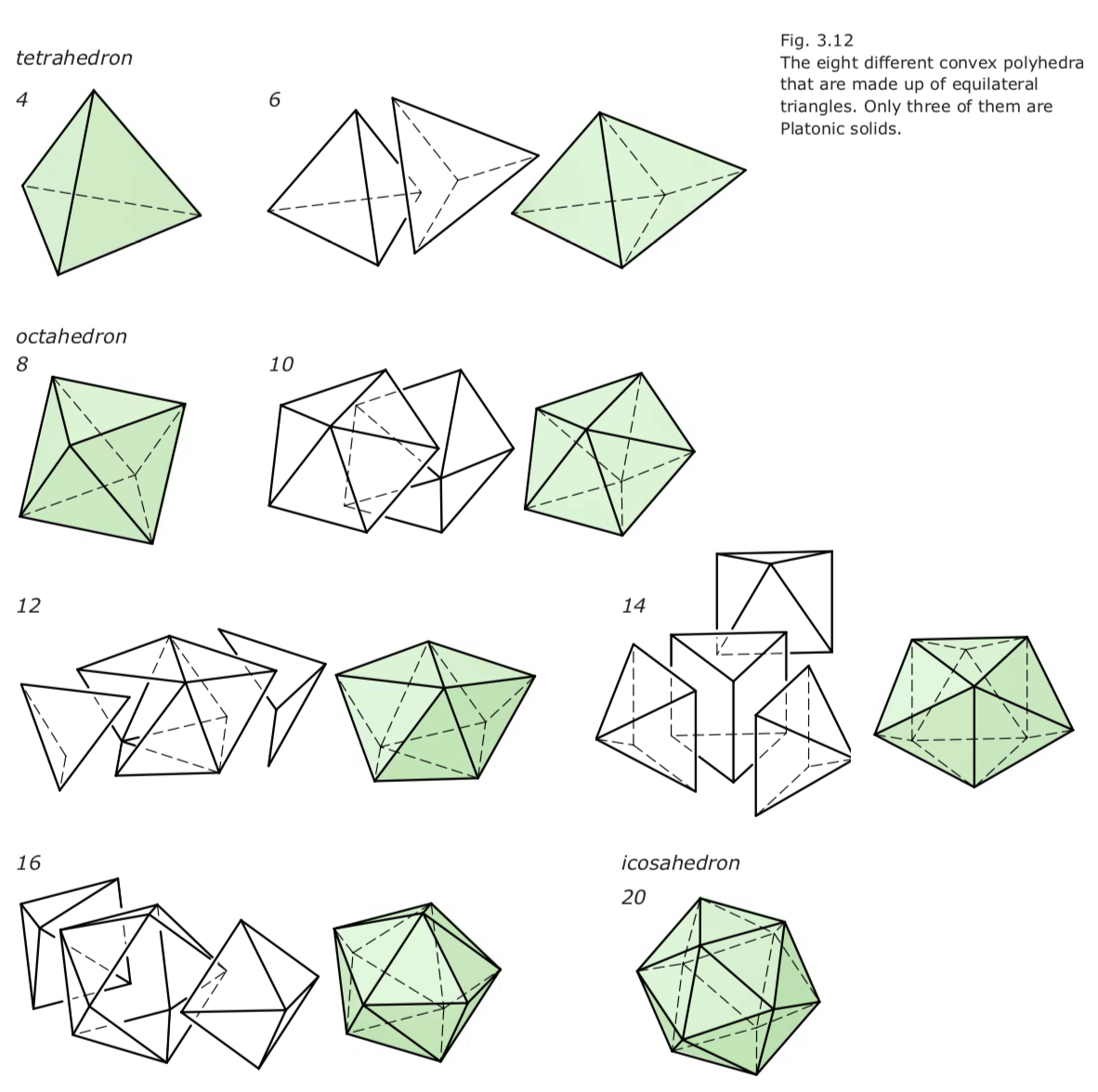
• 每个面都是全等三角的凸多面体：有8种，其中三个是tetrahedron, octahedron, icosahedron

Properties of Platonic solids

• Euler formula 欧拉公式 : v-e+f=2
• 柏拉图固体及其对偶dual：每个柏拉图固体的面中点作为格点构成另外柏拉图固体，称为固体的对偶
• 与柏拉图固体相关的球体：circumsphere外接球，insphere内切球，过边中点的球体
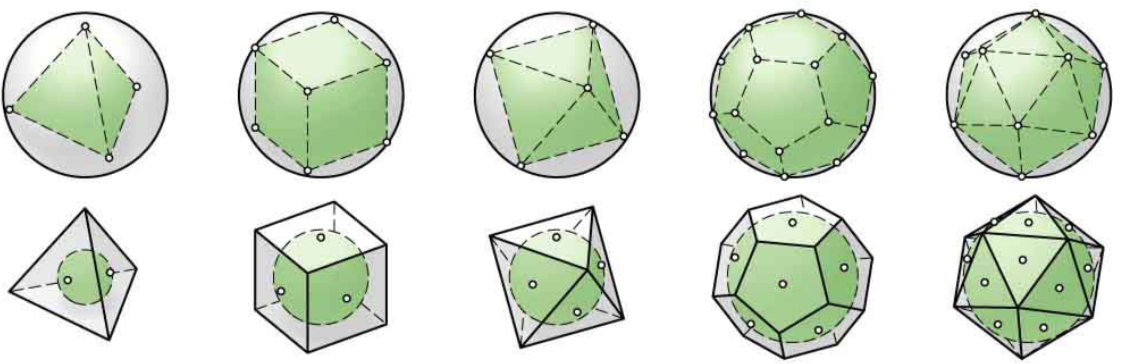
• 对称性质：1. 只有一种面；2. 所有边长相等；3. 临近面的二面角相等；4.所有格点棱锥全等

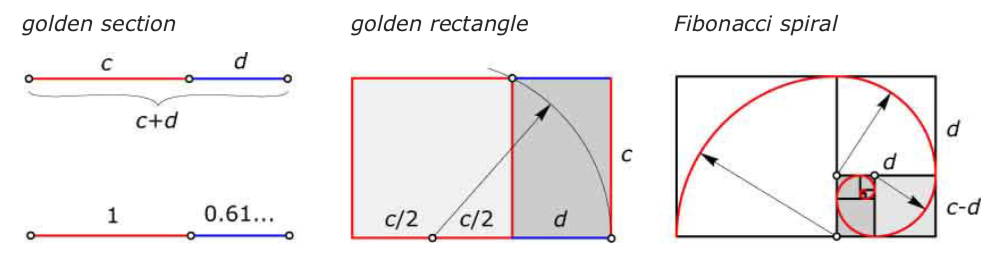
The goden section黄金分割比

• golden section=golden ratio=divine proportion
• $\varphi$= (1+$\sqrt5$)/2~=1.618033989; $\varphi^2-\varphi-1=0$
• The golden rectangel 黄金矩形：c:d=(c+d):c
• The Fibonacci spiral 斐波那契螺旋线：c:d=d:(c-d)

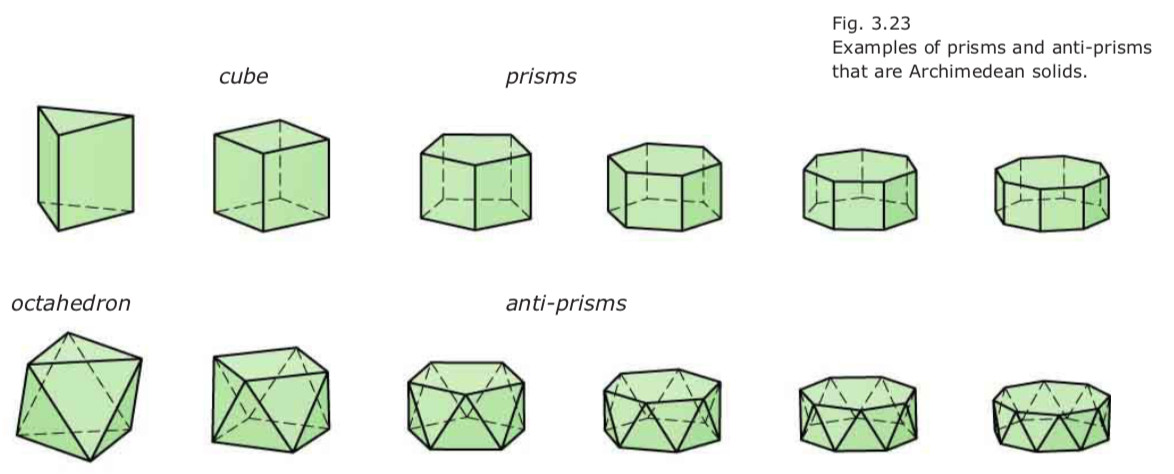
Archimedean solids 阿基米德固体

• 特性：1.所有边长相等；2.所有格点全等；3.每个面为正则多边形但是彼此不全等
• 由两种切割柏拉图固体角的办法变化得来：1.生成的正则多边形与原来边数相同；2.生成的正则多边形边数是原来的两倍
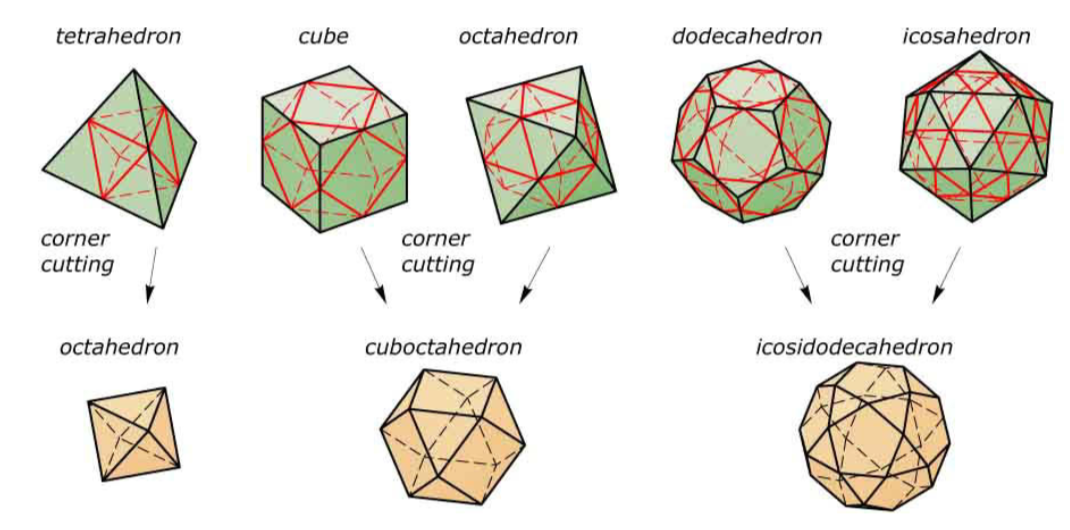
• 阿基米德固体13种(除棱柱和反棱柱外)：truncated tetrahedron, truncated cube, truncated octahedron,truncated docecahedron,truncated icodahedron……
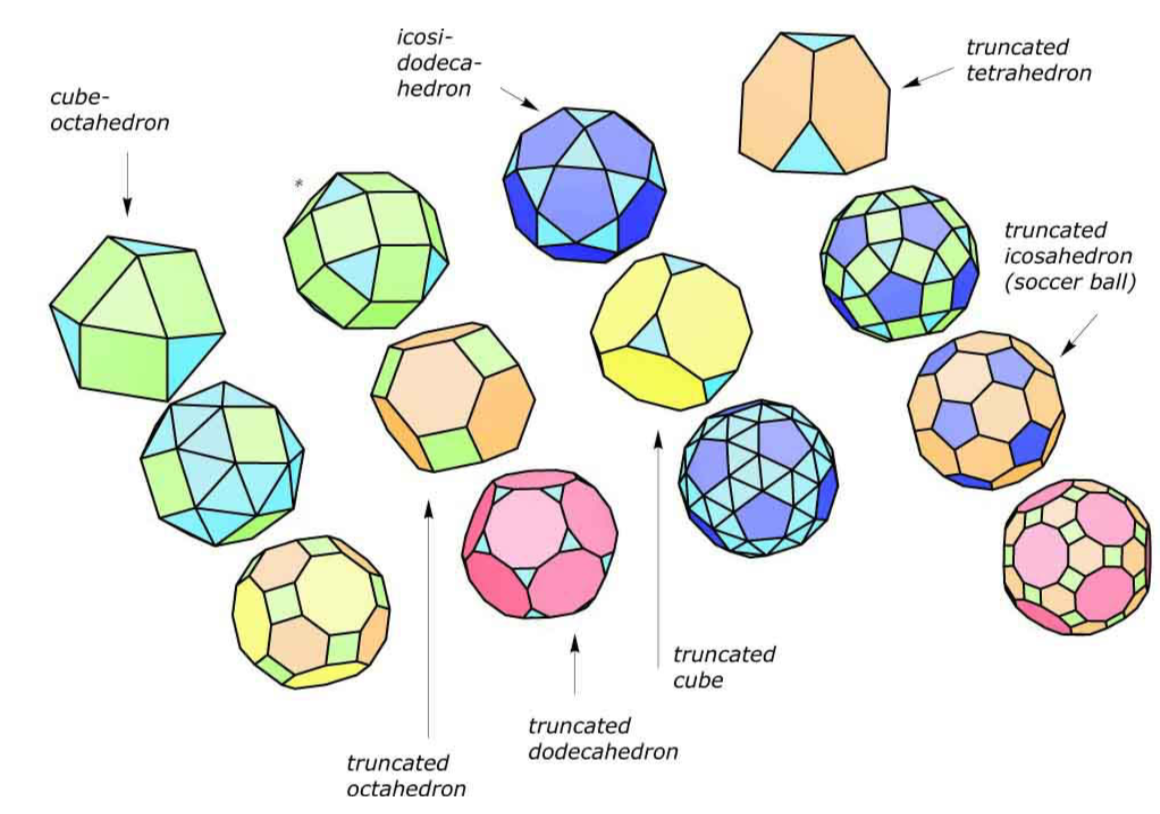
• prisms棱柱和anti-prisms反棱柱也是阿基米德固体
• prisms：上下地面为全等正则多边形，侧面是正方形
• anti-prisms：上下地面为经过旋转的全等正则多边形，侧面是三角形

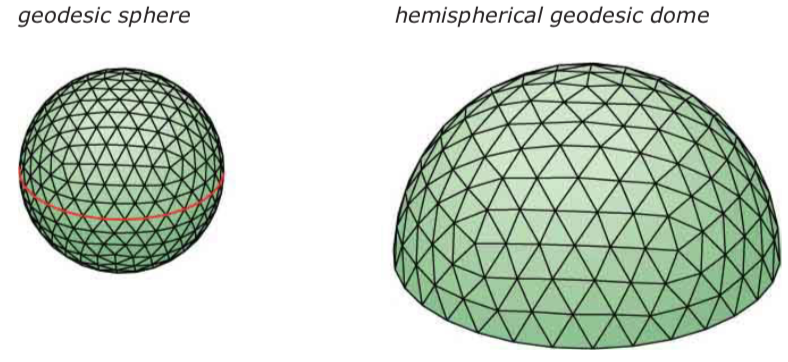
Geodesic spheres 测地球

• 测地球：所有格点位于同一球面的大圆上
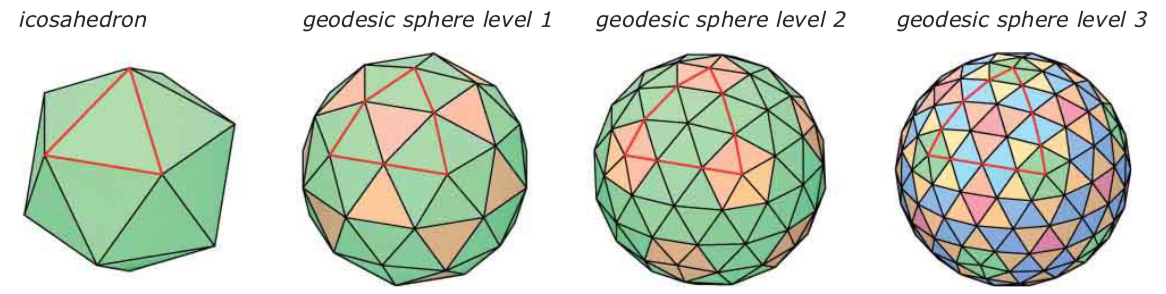
• 生成方法1：成指数(1,4,9,16,…)细分(subdivide)二十面体表面，再投影到外接球；得到三角形数目=$20\cdot(k+1)^2$.
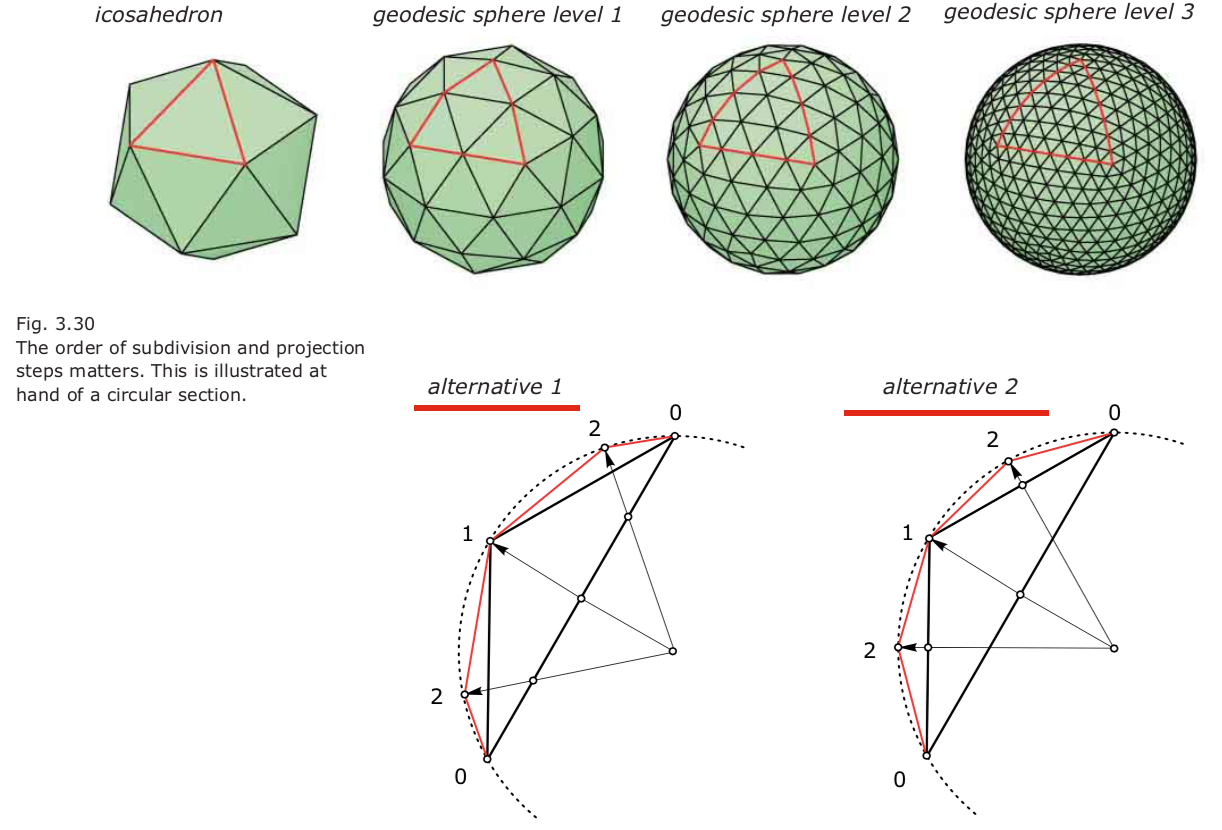
• 生成方法2：每一个三角形细分成4个全等三角形，再投影到外接球; 得到三角形数目=$20\cdot4^k$.

Space filling polyhedra 空间填充多面体

• cube立方体是唯一的柏拉图固体能完全填充3D空间
• 存在其他多面体完全填充空间
• 可以使用非全等多面体实现，但是复杂

Polyhedral surfaces

• If a smooth surface is approximated by a polyhedral surface we also speak of a discrete surface.
• 可以使用planar quadrilateral平面四边形实现对柱面和锥面的离散化
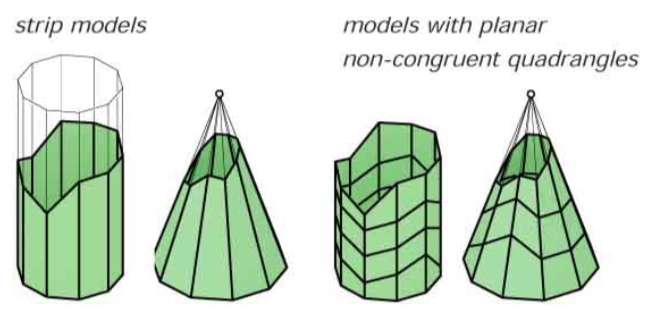
• 使用triangles三角近似freeform自由形曲面比平面多边形更容易
• The design of polyhedral freeform surfaces with planar faces other than triangles is a difficult task that is a topic of current research.