Planar transformation

• Important basic transformations are congruence transformations (translation, rotation, reflection), which preserve all lengths and angles occurring on an object. 平移、旋转、对称三个基本变换保长+保角。

Translation, Rotation, and Reflection in the Plane 平面上的平移、旋转、对称变换

• The congruence transformations are also called isometries. 全等变换=等距变换
• Direct congruence transformation 直接全等变换：平移、全等、自变换
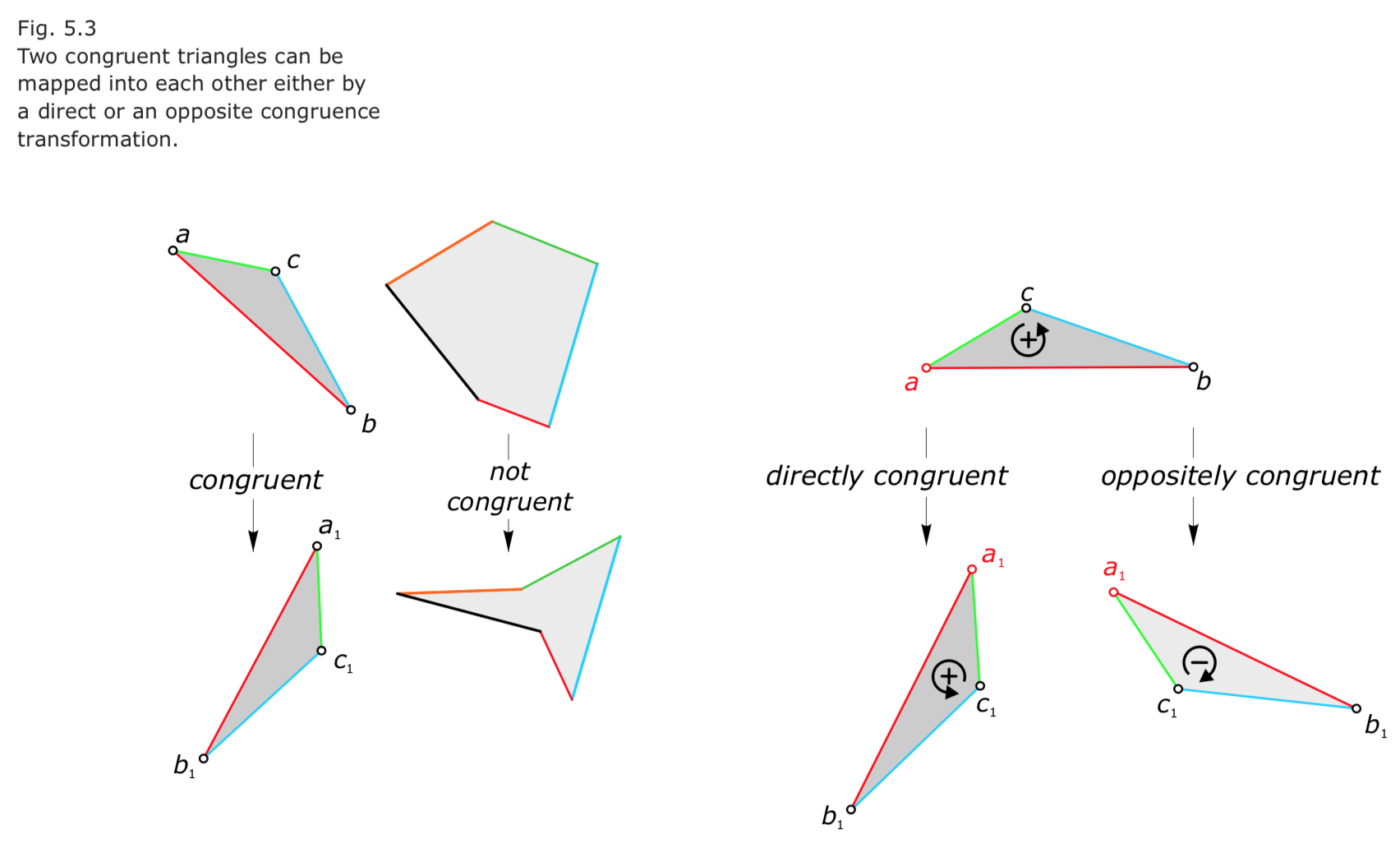
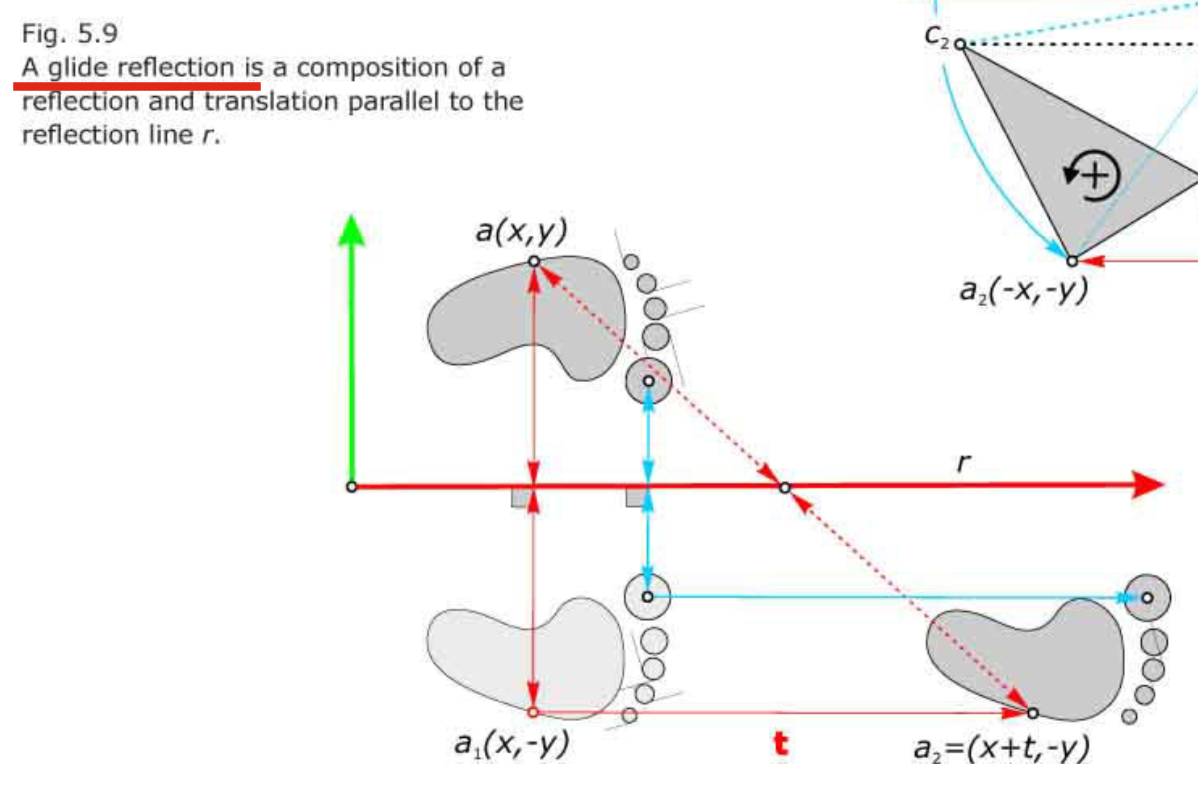
• Oppositely congruence transformation 相对全等变换：反射、glide reflection

Scaling and shear transformations

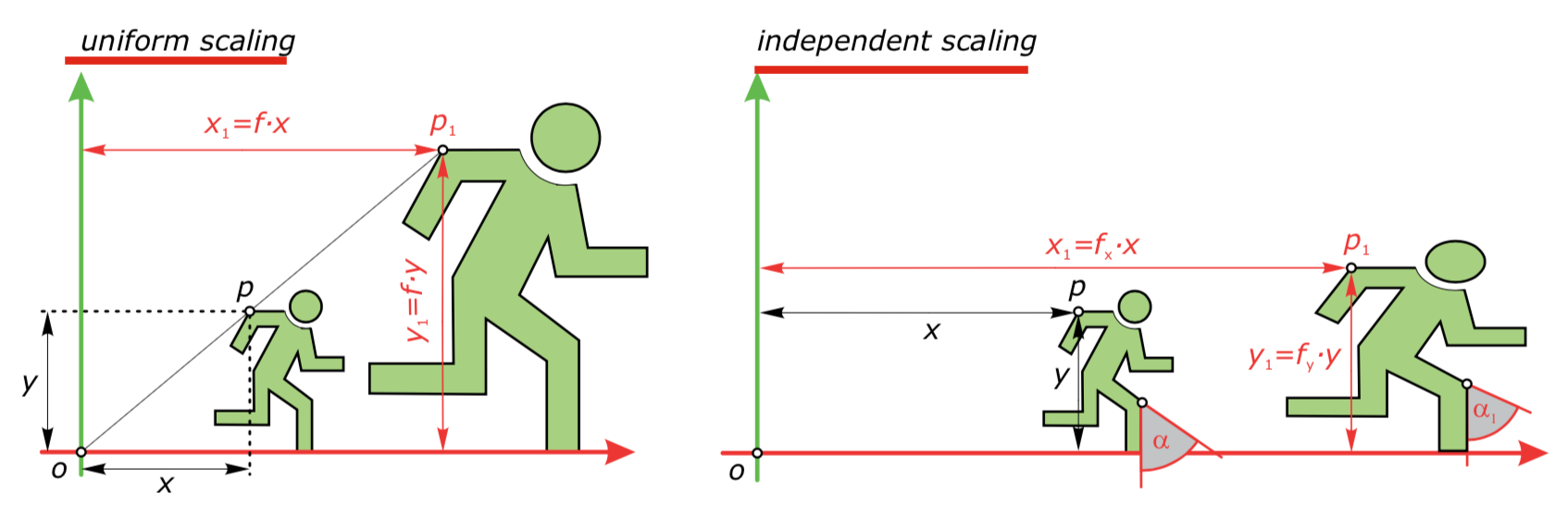
• Uniform Scaling 均匀放缩 由一个放缩比例$f_x$ 或 $f_y$决定
• Independent Scaling 独立放缩 两个放缩比例$f_x$,$f_y$决定，特别地，$f_xf_y=1$ 为报面积变换
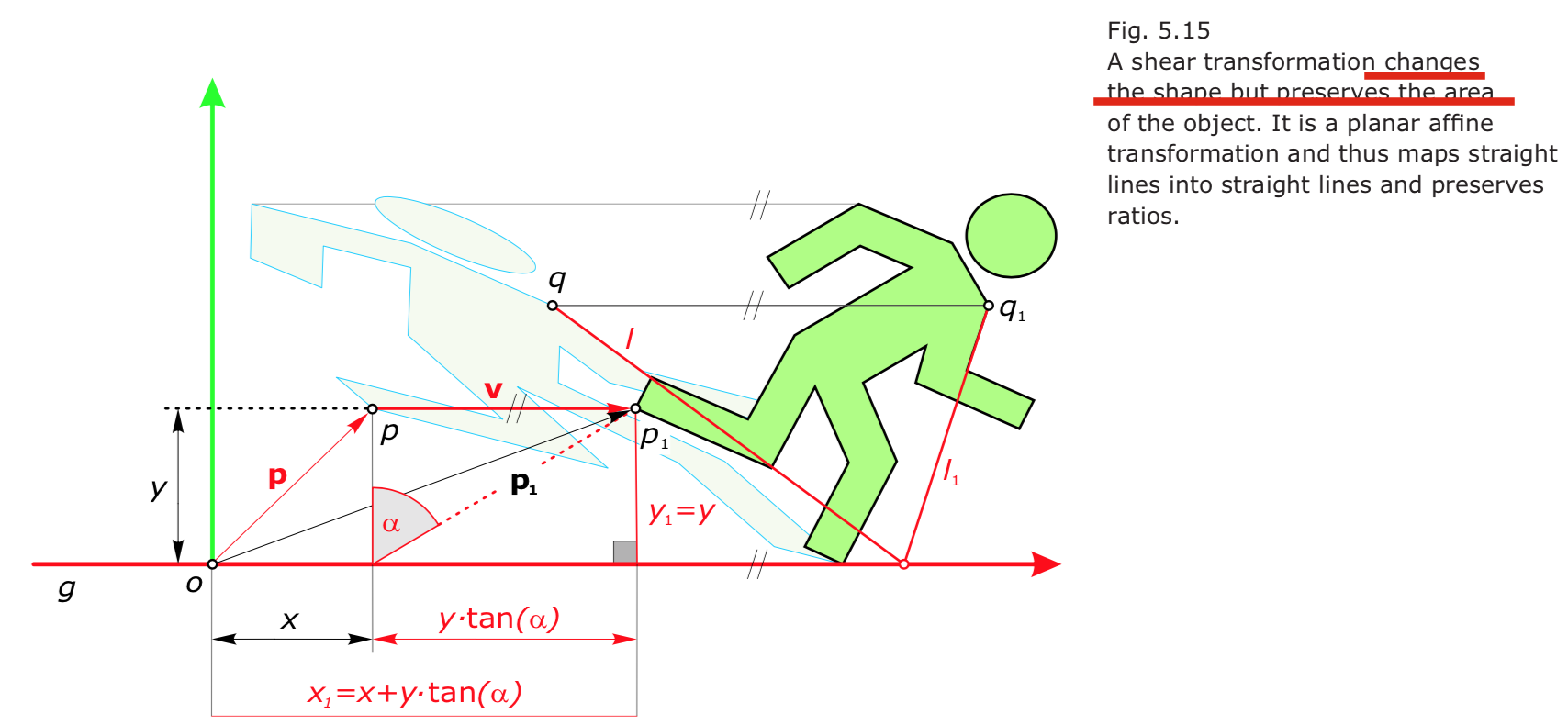
• Shear transformation 改变物体形状，但是保面积

Tilings ~ Tessellation 贴图

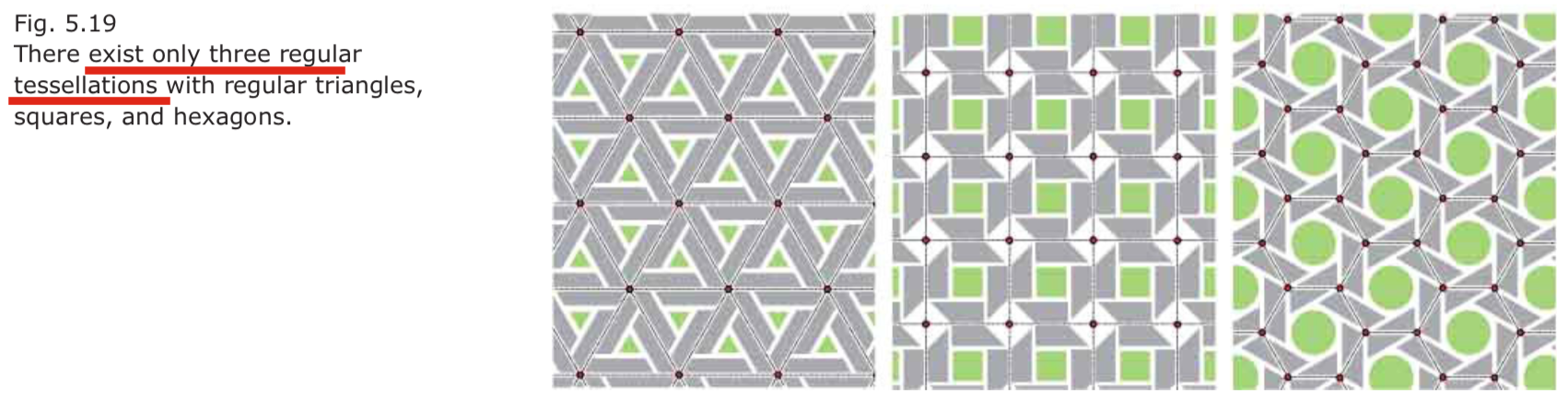
• regular tessellations 规则贴图 只有三种：triangles三角、squares四边、hexagons 六边
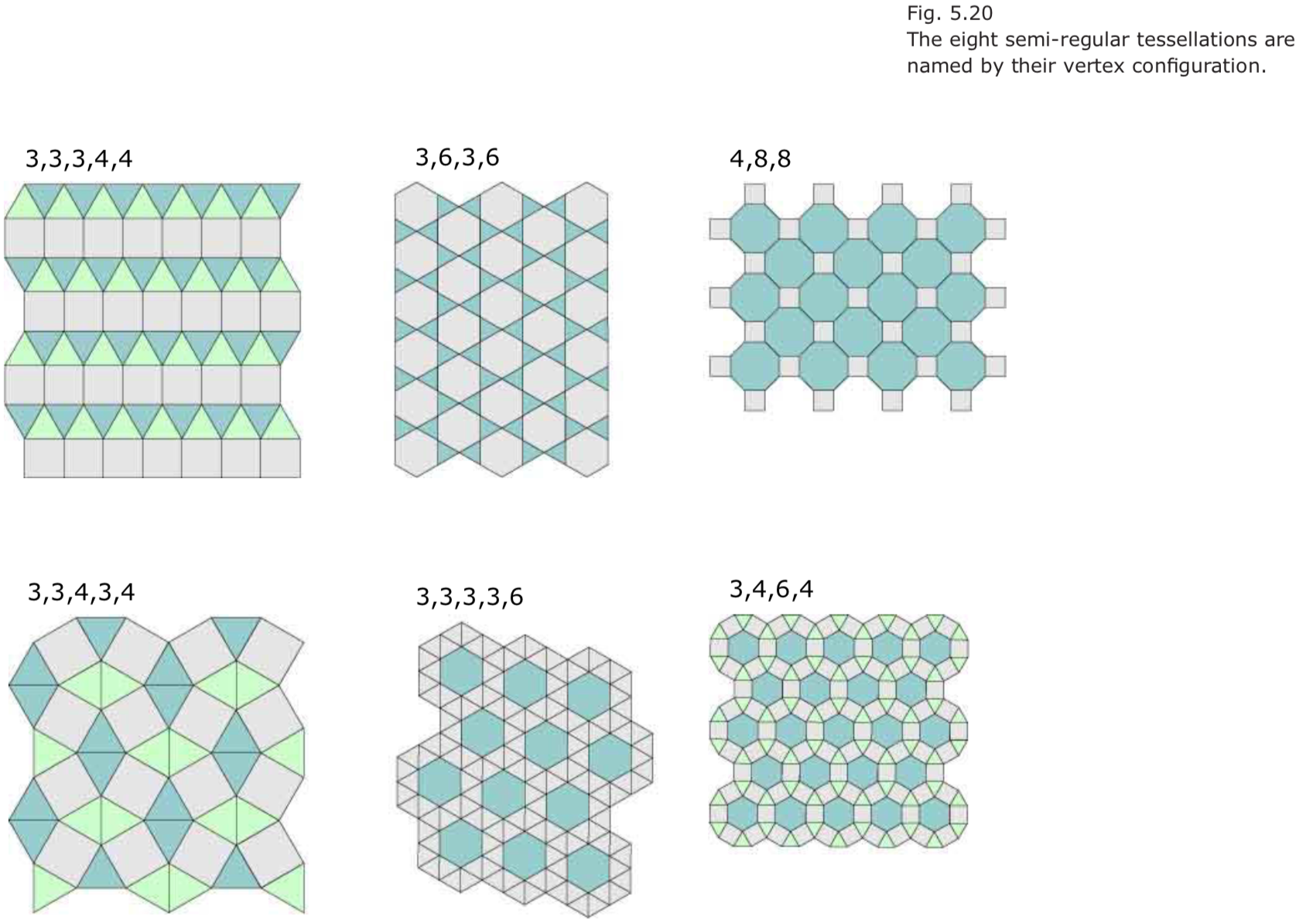
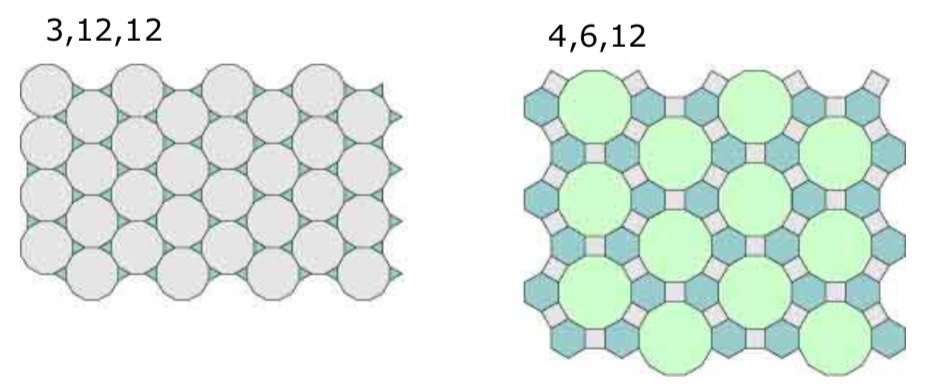
• semi-regular tessellations 半规则贴图 由非单一正则多边形组成，每个节点有相同的组合形式；共8个
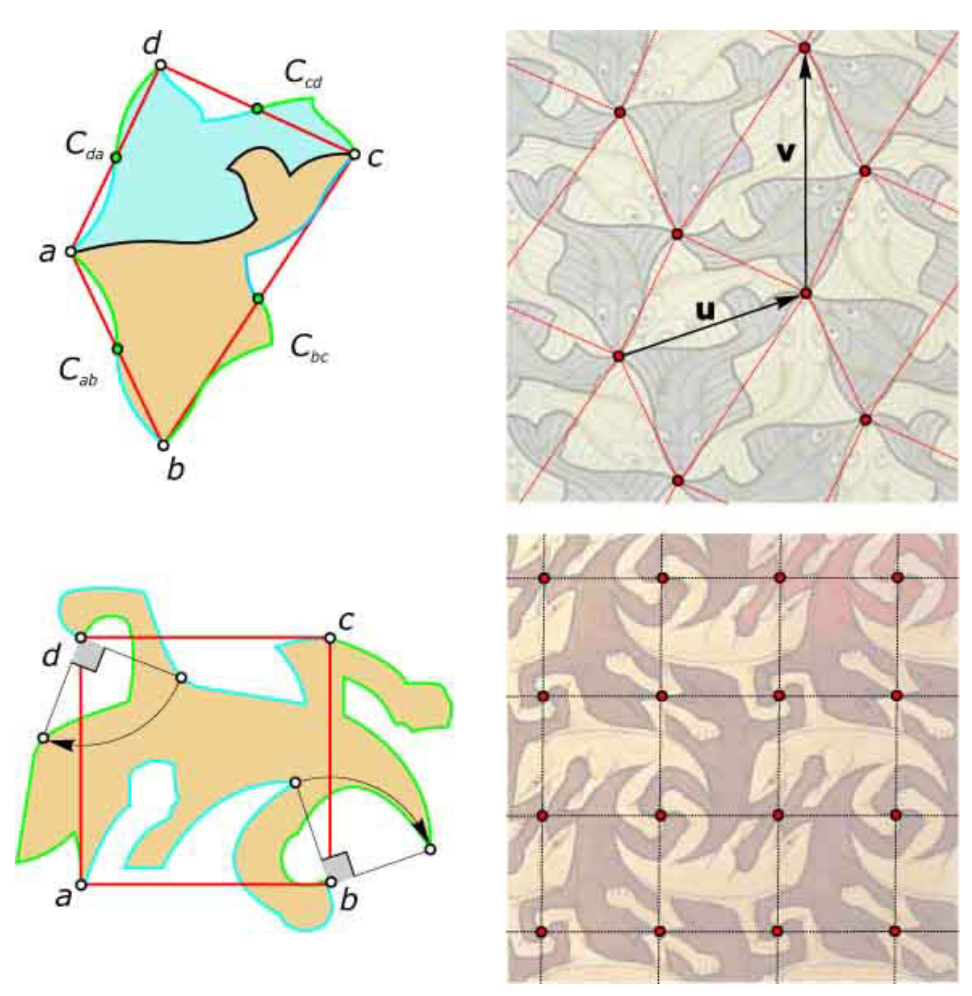
• Translations, rotations, reflections, and glide reflections are the only transformations that can be applied on patterns without changing the pattern.

Nonlinear transformation in 2D

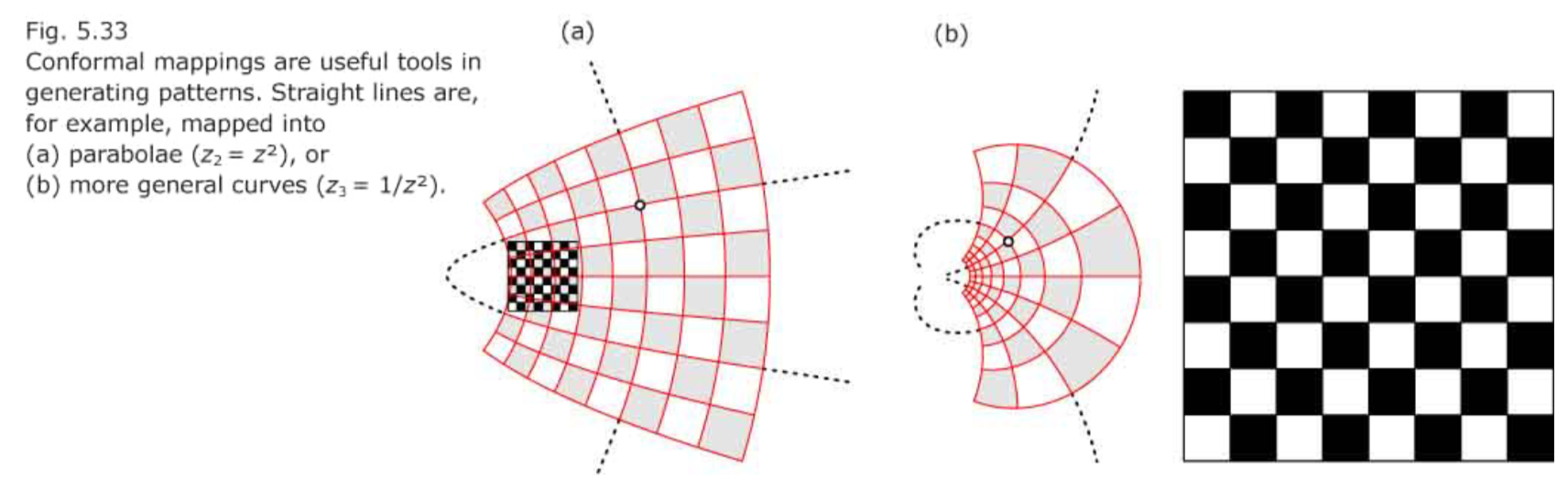
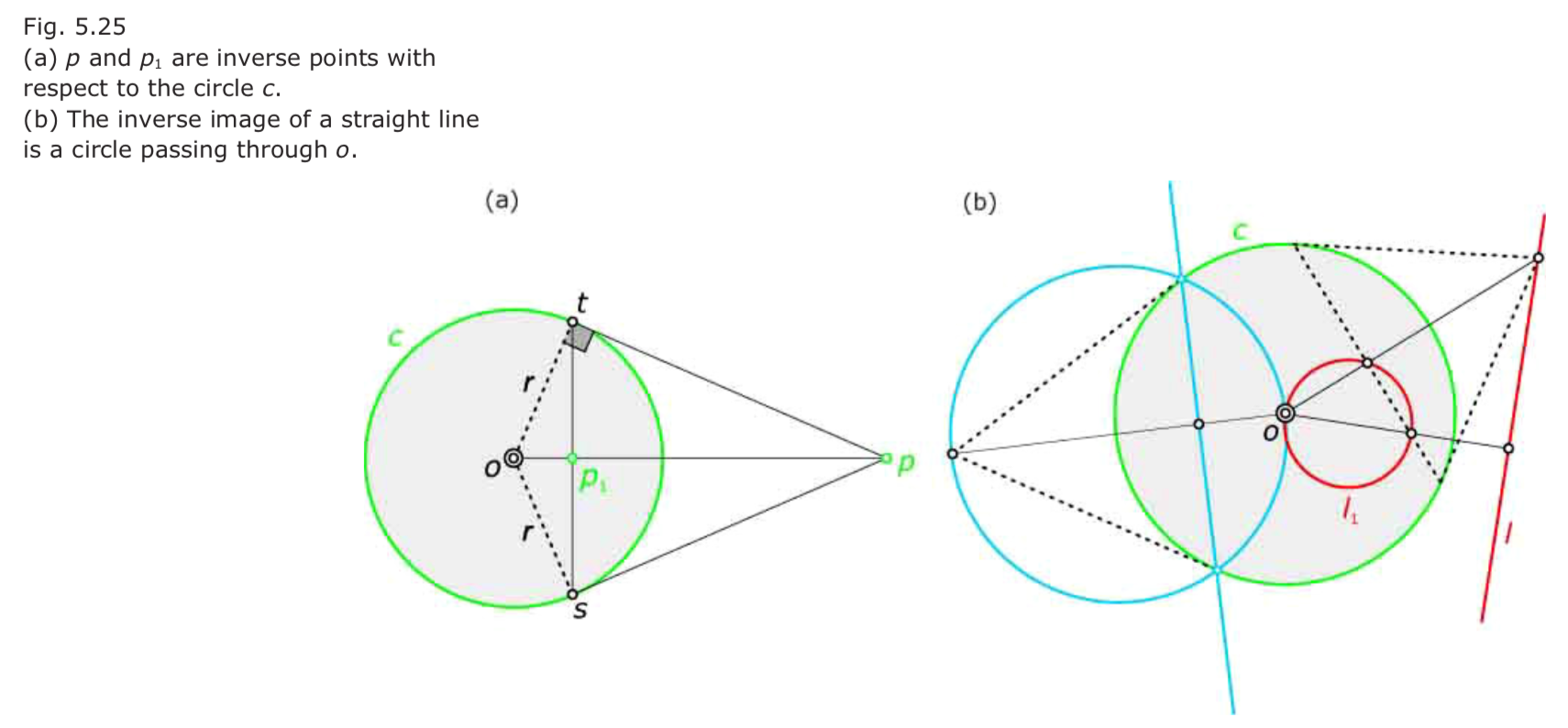
• Nonlinear transformation 将直线映射成圆
• reflection along a circle：inversion ~ division 逆运算
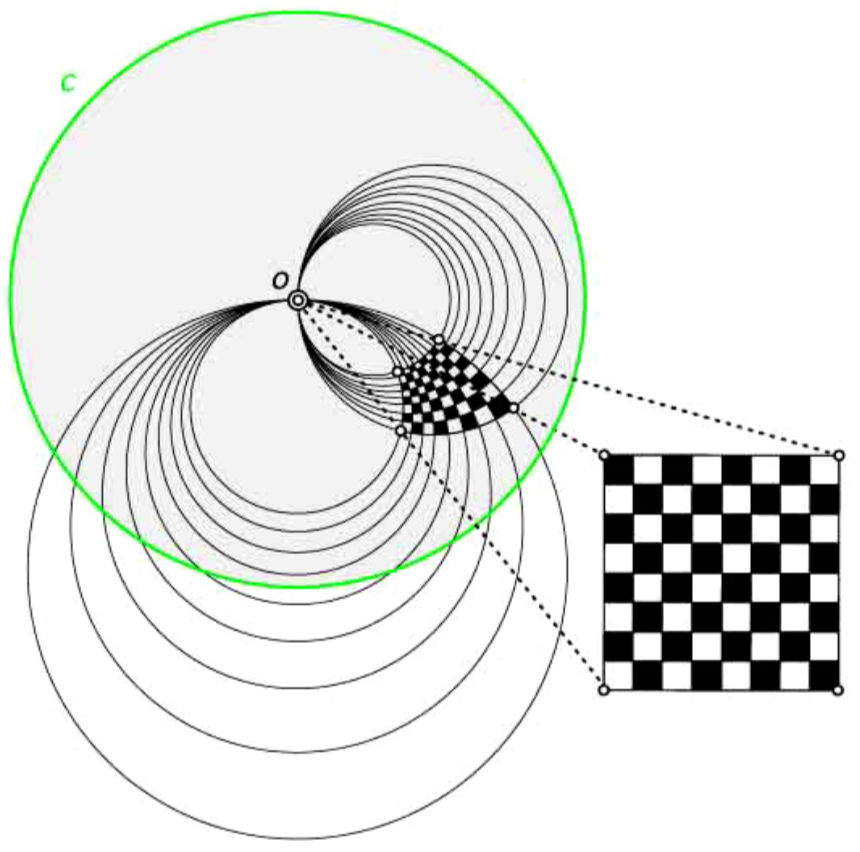
• Möbius transformations. The transformation $z2 = \frac{r^2}{\bar{z}}$ is a special case of so-called Möbius transformations, which are defined by $z_1 = \frac{a\cdot \bar{z}+b}{c\cdot \bar{z}+d}$ or $z_1 = \frac{a\cdot {z}+b}{c\cdot{z}+d}$ with a, b, c, and d as arbitrary complex numbers.
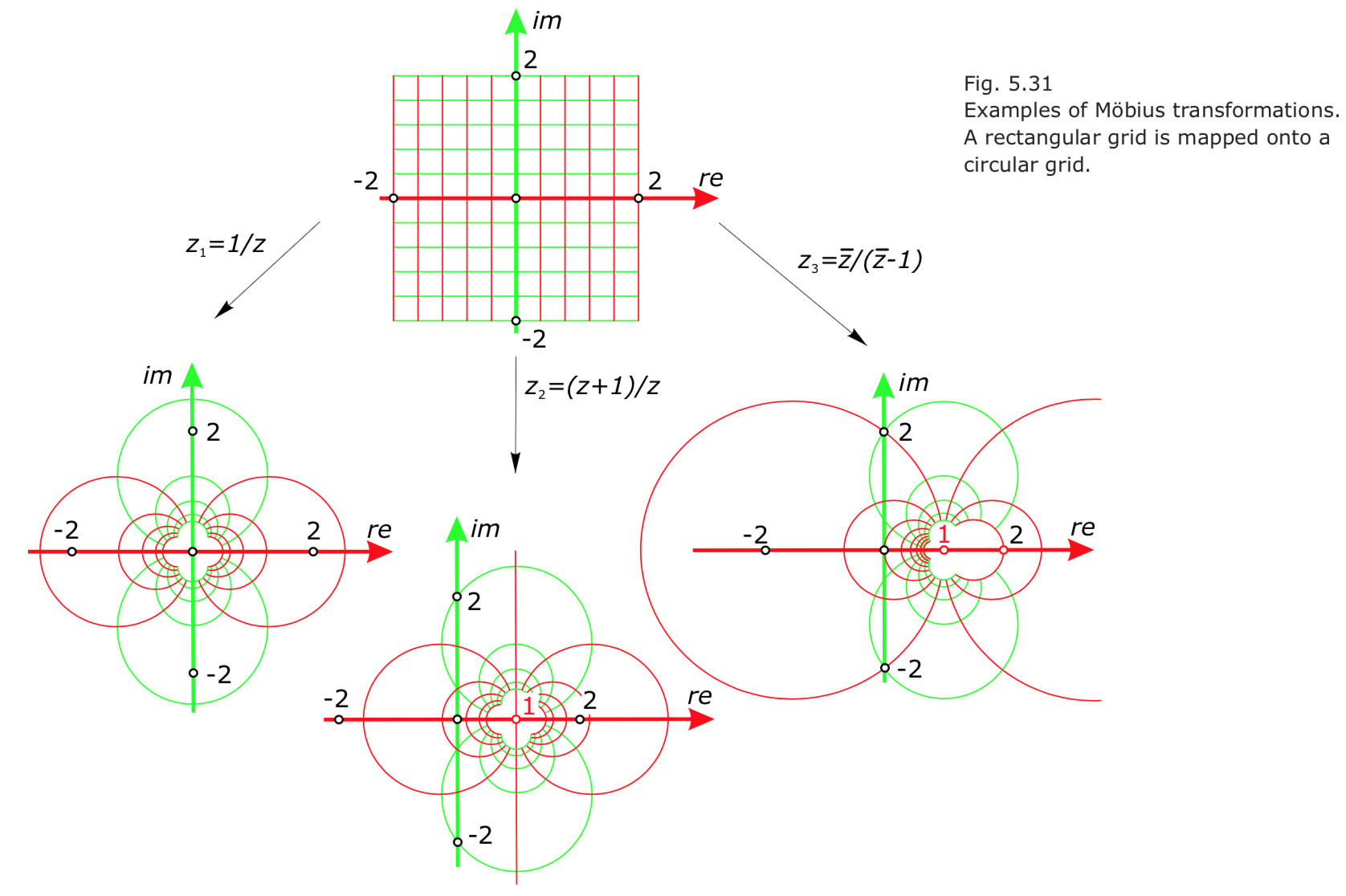
• Circles are mapped onto straight lines or circles. 所有Möbius变换将圆映射成圆
• The intersection angle of two curves is preserved. 保角变换
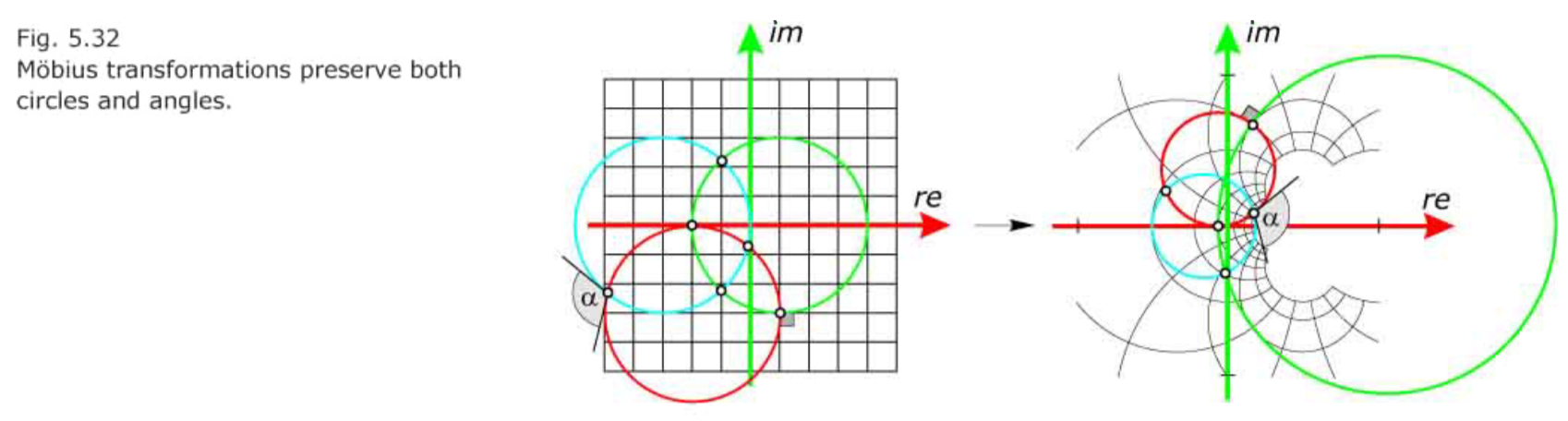
• If we waive the circle-preserving property but insist on the preservation of angles, we have the set of conformal transformations.