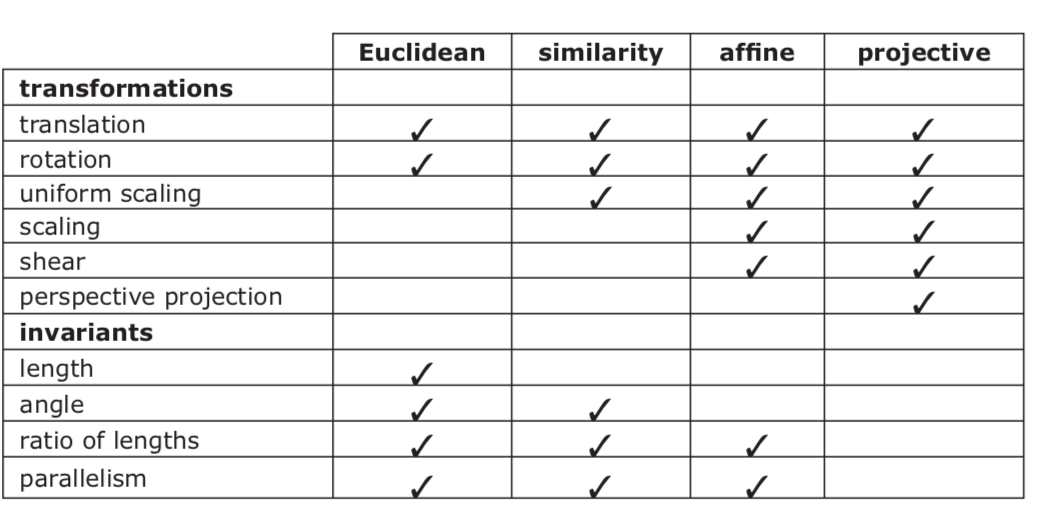
Translation, rotation and reflection in space空间中的平移、旋转和对称变换

• spatial congruence transformations: 空间全等变换保shape形状，保distance距离
• 分两类:
  1. direct congruence transformation (右手坐标架right-handed coordinate frame)，
  2. opposite congruence transformation (left-handed coordinate fram)
• translation 平移

  x1 =x+a,
  y1 =y+b,
  z1 =z+c,

• rotation 旋转
  关于z-axis旋转：

x1 = x · cos ρ – y · sin ρ,
y1 = x · sin ρ + y · cos ρ,
z1 = z

关于x-axis旋转：

x1 = x,
y1 = y · cos ρ – z · sin ρ,
z1 = y · sin ρ + z · cos ρ,

关于y-axis旋转：

x1 = x · cos ρ + z · sin ρ,
y1 = y,
z1 = –x · sin ρ + z · cos ρ.

• reflection反射

• glide reflection 滑动对称：先对称在平移；是direct congruence变换；

  x1 =x+a,
  y1 =y+b,
  z1 = –z.

• One can prove that the composition of a reflection and a rotation is always a single glide reflection or a simple reflection. 对称和旋转变换的复合总是一个简单的滑动对称或简单的对称变换。

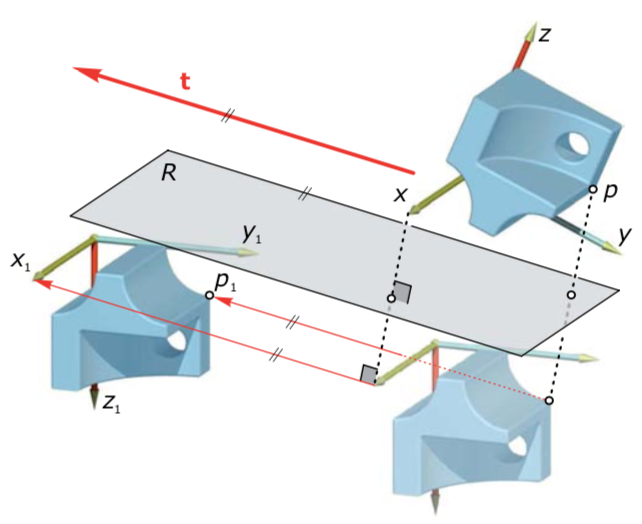
Helical transformation 螺旋变换

• The most general opposite congruence transformation is the glide reflection, a combination of a reflection and a special translation. 滑动对称是最一般的相对全等变换，是对称和平移变换的复合。
• The helical transformation, as the direct congruence counterpart to the glide reflection, is the composition of a rotation about the helical axis A and a translation parallel to this axis. 螺旋变换是滑动对称变换，关于螺旋轴旋转再复合关于螺旋轴方向的平移。

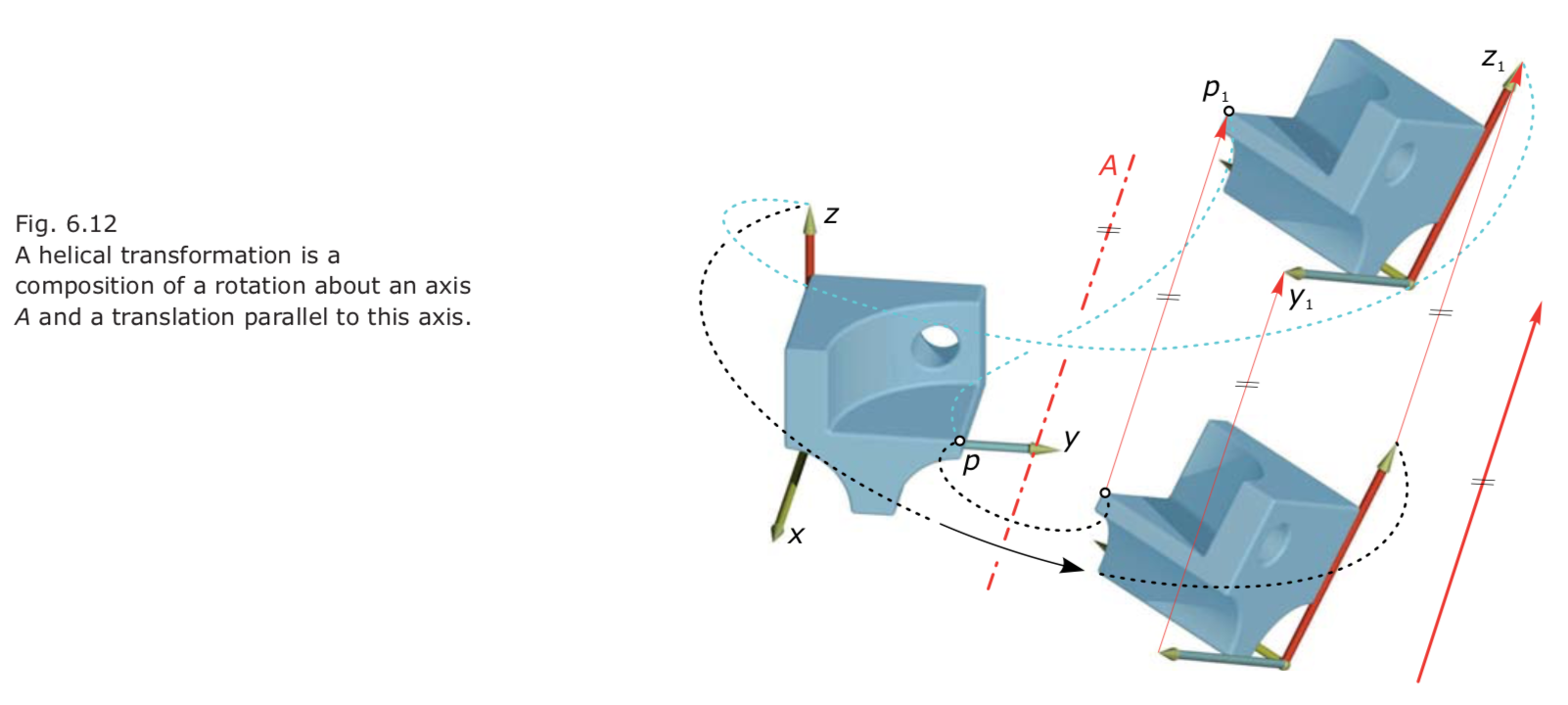
• Given any two distinct (directly congruent) positions of a rigid body, we can always find a unique helical transformation that transfers one position to the other. 一个刚体的任何两个位置之间的变换，都可以找到唯一的螺旋变换。

  x1 = x · cos ρ – y · sin ρ,
  y1 = x · sin ρ + y · cos ρ,
  z1 =z+p·ρ.

• 螺旋变换好的性质：

1. Every helix lies on the surface of a rotational cylinder F. The axis of this supporting cylinder is the helical axis.
2. The angle α between the tangents of all points of the helix and a normal plane of the axis is constant.
3. As a consequence, when we cut the supporting cylinder along a straight line (parallel to the axis) and unfold the cylinder into a plane the helix $c^d$ becomes a straight line cd in this planar development $F^d$.
4. If we apply to a helix the generating helical motion, it moves in itself (as a whole). This is important for the working effect of screws.

　　　　　　　　　　　Fig. 最美修道院

　　　　　　　　　　　Fig. 拍摄于奥地利Melk修道院

Smooth motions and animation 光滑运动和动画

• three basic scenarios:

1. 固定摄像机移动物体；
2. 固定物体，移动摄像机；
3. 摄像机和物体都移动。

Affine transformation 仿射变换

\(x1 =a·x+b·y+c·z+u,\)
\(y1 =d·x+e·y+f·z+v,\)
\(z1 =g·x+h·y+i·z+w.\)

性质：

1. Straight lines are mapped into straight lines.
2. Planes are mapped into planes.
3. Parallel lines (planes) are transformed into parallel lines (planes).
4. The ratio of the lengths of two line segments on parallel lines is preserved during the transformation.

• Parallel projection is also a special case of an affine transformation—where three-dimensional space is mapped into a plane.
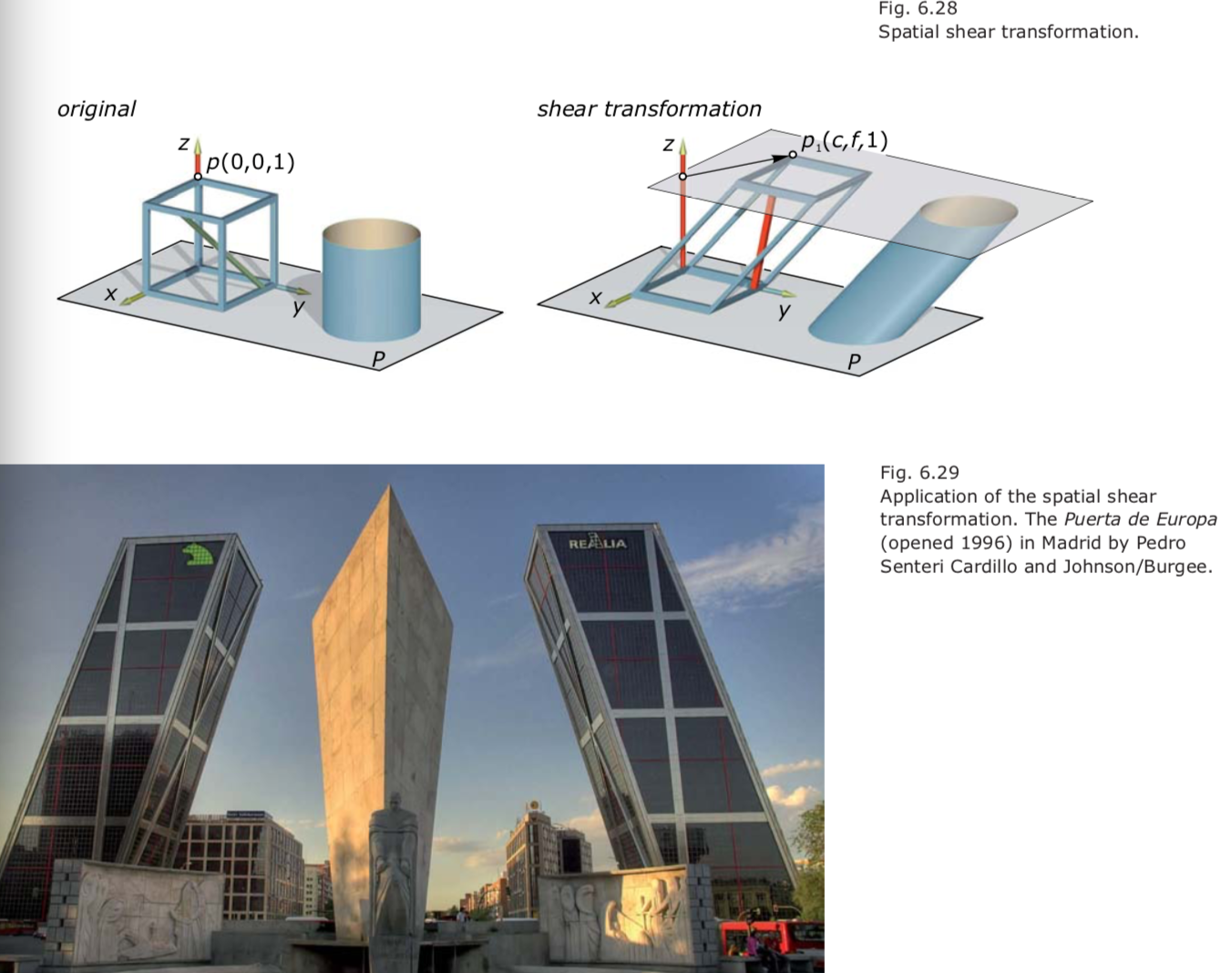
• shear transformation ：

  \(x_1=x+c\cdot z;\)
  \(y_1=y+f\cdot z;\)
  \(z_1=z.\)

• spiral transformation:

  \(x1 = k(ρ)·x·cos ρ – k(ρ)·y·sin ρ,\)
  \(y1 = k(ρ)·x·sin ρ + k(ρ)·y·cos ρ,\)
  \(z1 = k(ρ)·z,\)
  \(k(ρ) = epρ.\)

Projective transformation

• Affine transformations constitute the class of linear transformations (i.e., line- preserving) that maps parallel lines into parallel lines.

• Degenerate here means that a parallel projection maps three-dimensional space to a two-dimensional plane, whereas nondegenerate affine transformations map spatial objects into spatial objects.
• Parallel projection maps certain lines (namely, projection rays) into points, whereas general affine transformations always map straight lines into straight lines.
• The perspective projection maps three-dimensional space into a two-dimensional plane. Most straight lines are mapped to straight lines, an exception being projection rays (which are mapped into points).
• General projective transformations map three-dimensional space into three- dimensional space such that any straight line is mapped into a straight line.

• General projective transformations do not preserve lengths, angles, parallelism, or ratios.

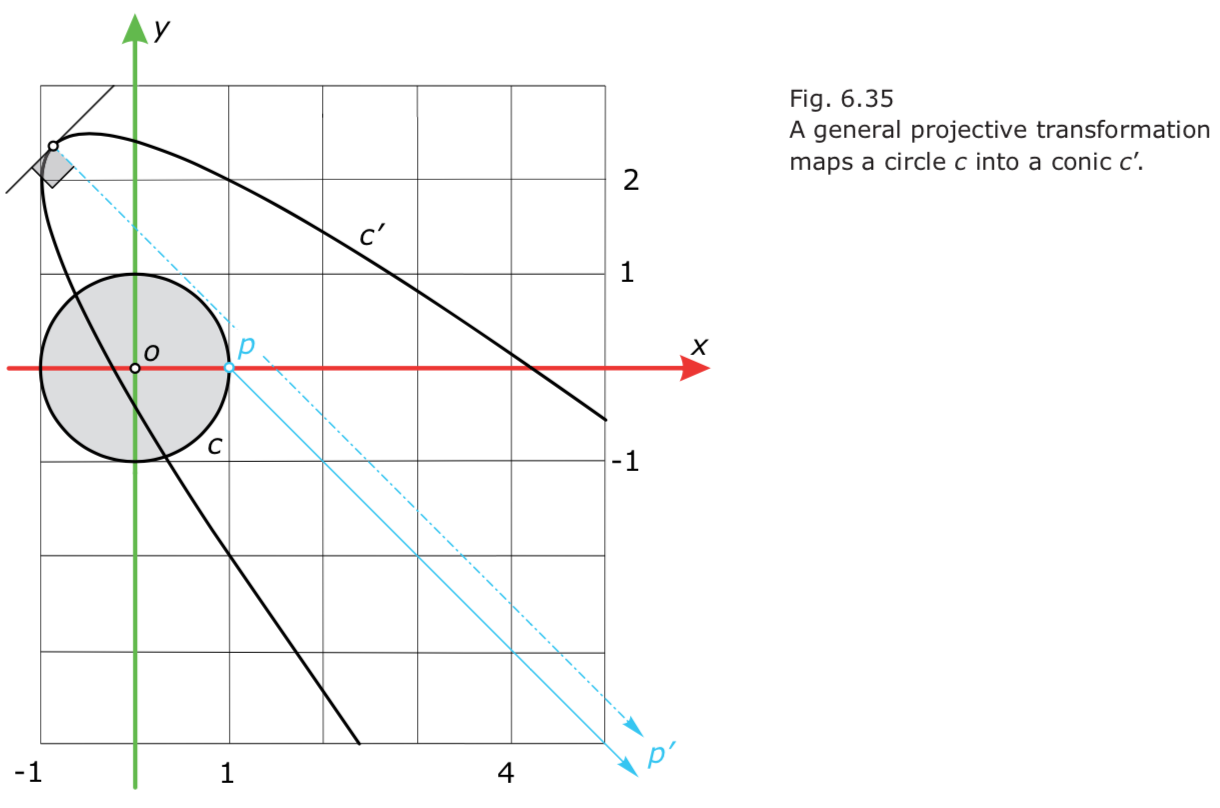
• Projective imalges of circles: The image of a circle c under a projective transformation is always a conic: an ellipse (including the case of a circle), a parabola, or a hyperbola.

• Planes H that intersect along two rulings ~ All planes parallel to a plane H cut the cone along a hyperbola.
• Planes P that touch along one ruling ~ All planes parallel to a plane P intersect the cone along a parabola.
• Planes E that intersect only at the vertex of the cone ~ All planes parallel to a plane E intersect the cone along an ellipse.