Curves 曲线

• All points of a circle or a conic section lie in a plane. These curves are called planar curves, in contrast to spatial curves such as helixes. 如下图，维也纳Karl教堂两个柱子上的纹路，就是螺旋线：

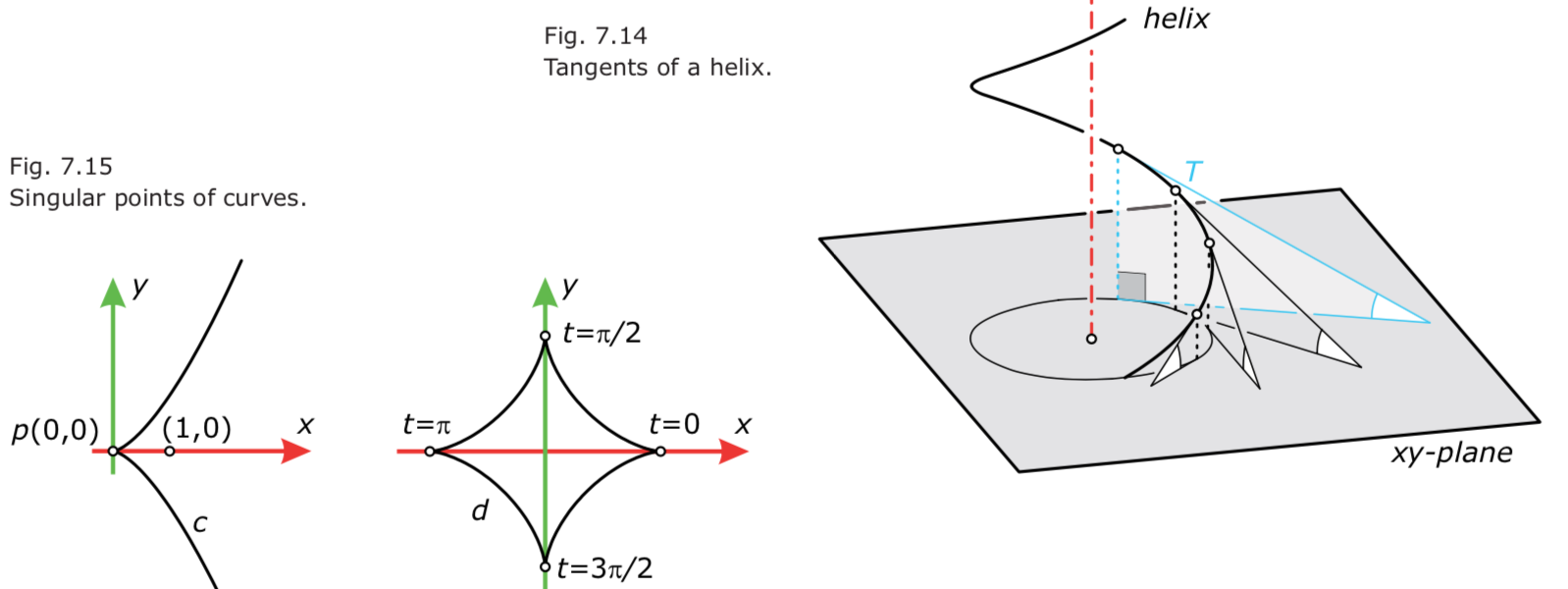
• Points of the curve with a uniquely defined tangent are called regular points. All points where the tangent vector $c’(t)$ is a non-vanishing vector are regular points. Curve points where $c’(t)$ is the zero vector $o$ are singular points. 下图是奇异点、螺旋线的切线与平面成定角：

• discrete curve 离散曲线：The polygon is also called a discrete curve. In many practical computations, curves are actually polygons (i.e., discrete curves). 离散曲线就是折线。

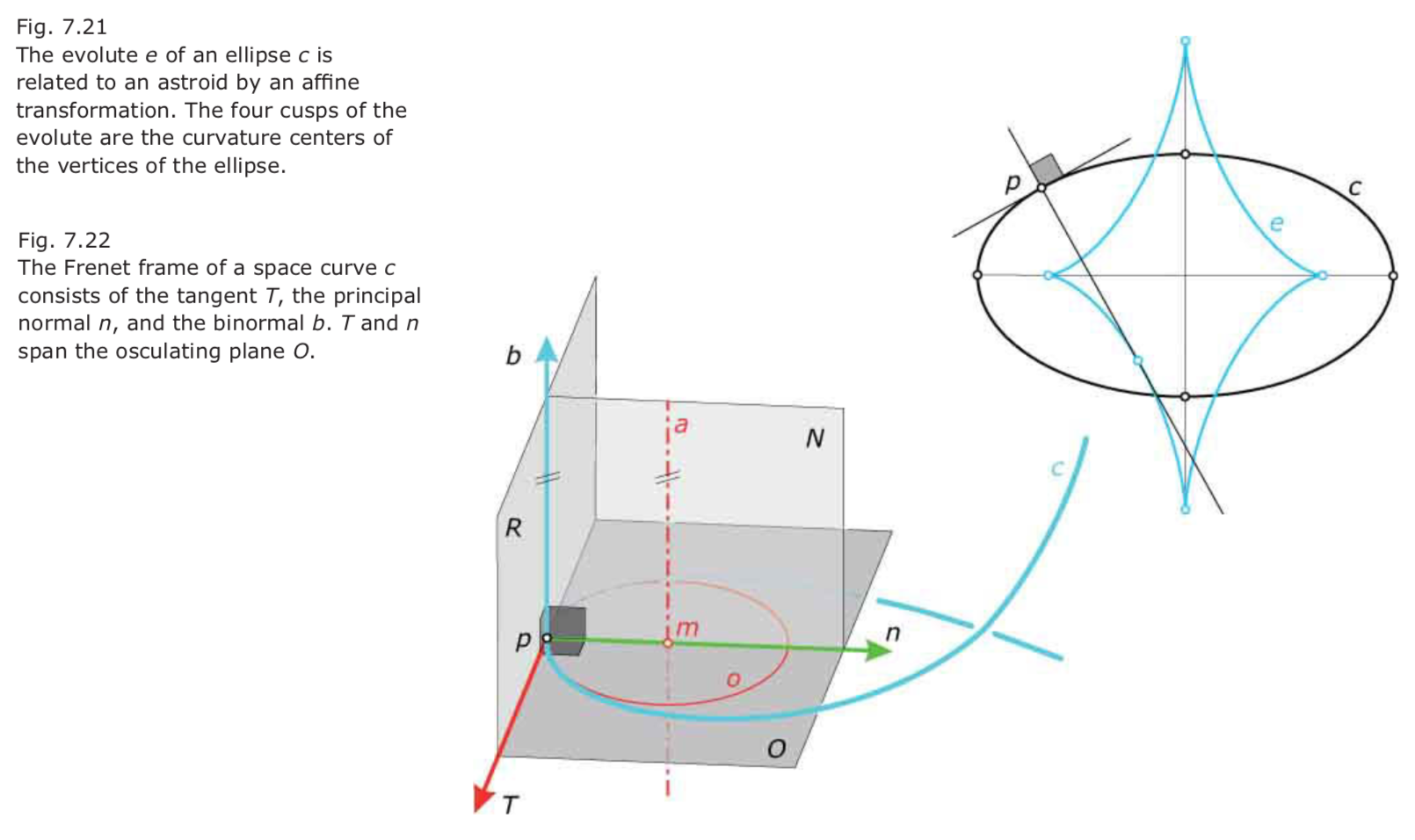
• 下图是椭圆线的密切圆中心轨迹即evolute、Frenet标架，osculating circle密圆、principle normal主法向量，binomial副法向量：

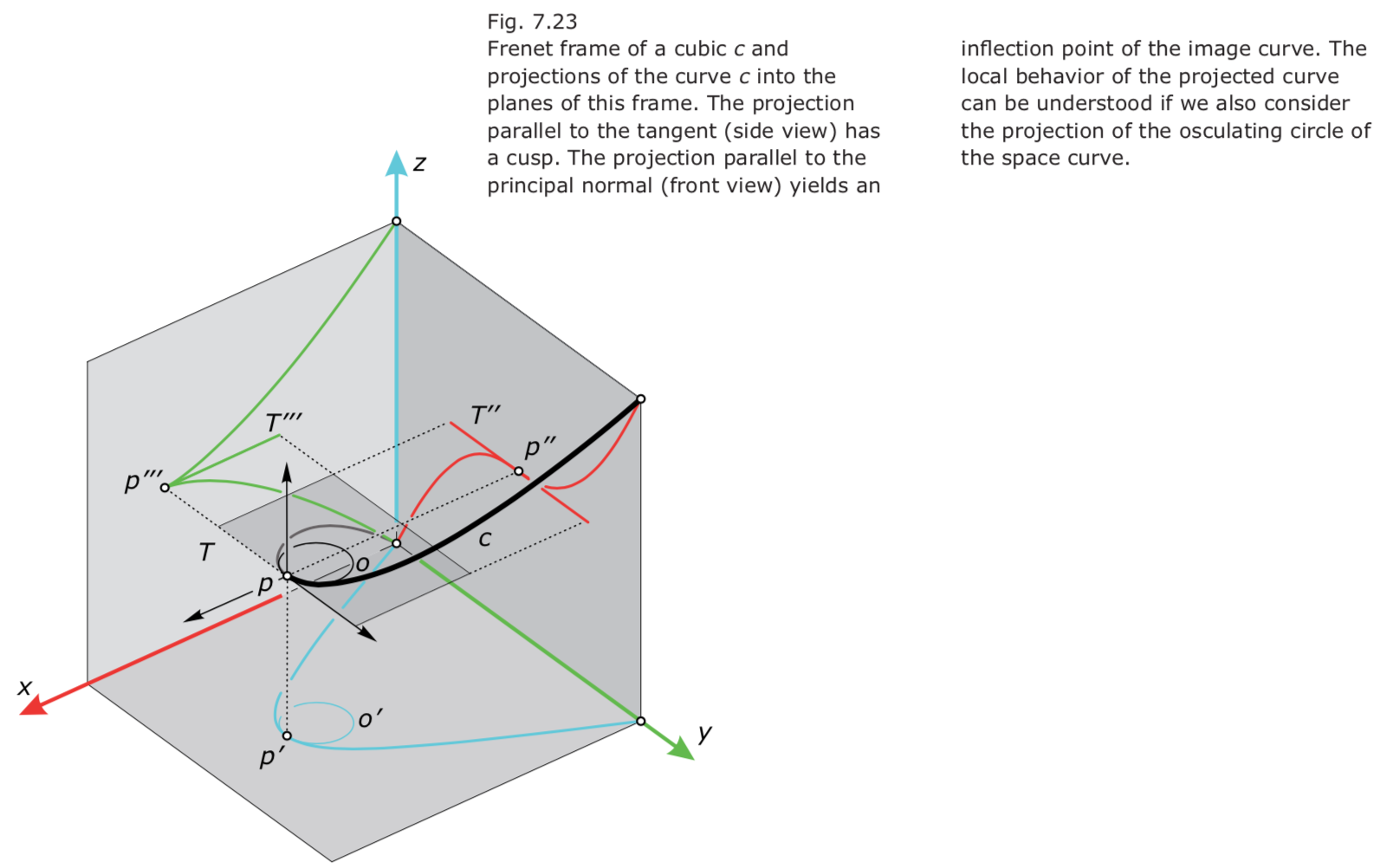
• 从切平面方向（与密切平面垂直方向）的投影是几乎光滑曲线(蓝线)，密切平面方向在yz平面投影有拐点inflection point（红线），在xz平面有尖点cusp（绿线）：

Conic sections 锥部分

• implicit representation隐式表示：$a·x^2 + b·x·y + c·y^2 + d·x + e·y + f = 0.$
• ellipse 椭圆： $b^2·x^2 + a^2·y^2 – a^2·b^2 = 0$; 找椭圆的密切圆圆心构图方法：

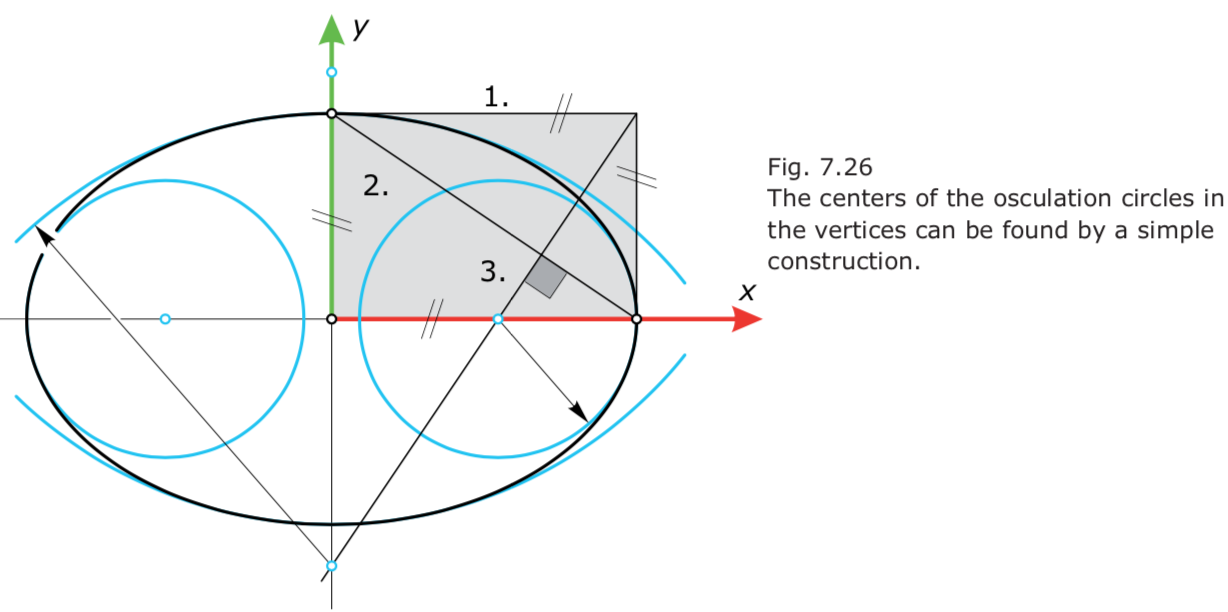
• hyperbola 双曲线：$b^2·x^2 – a^2·y^2 – a^2·b^2 = 0$;

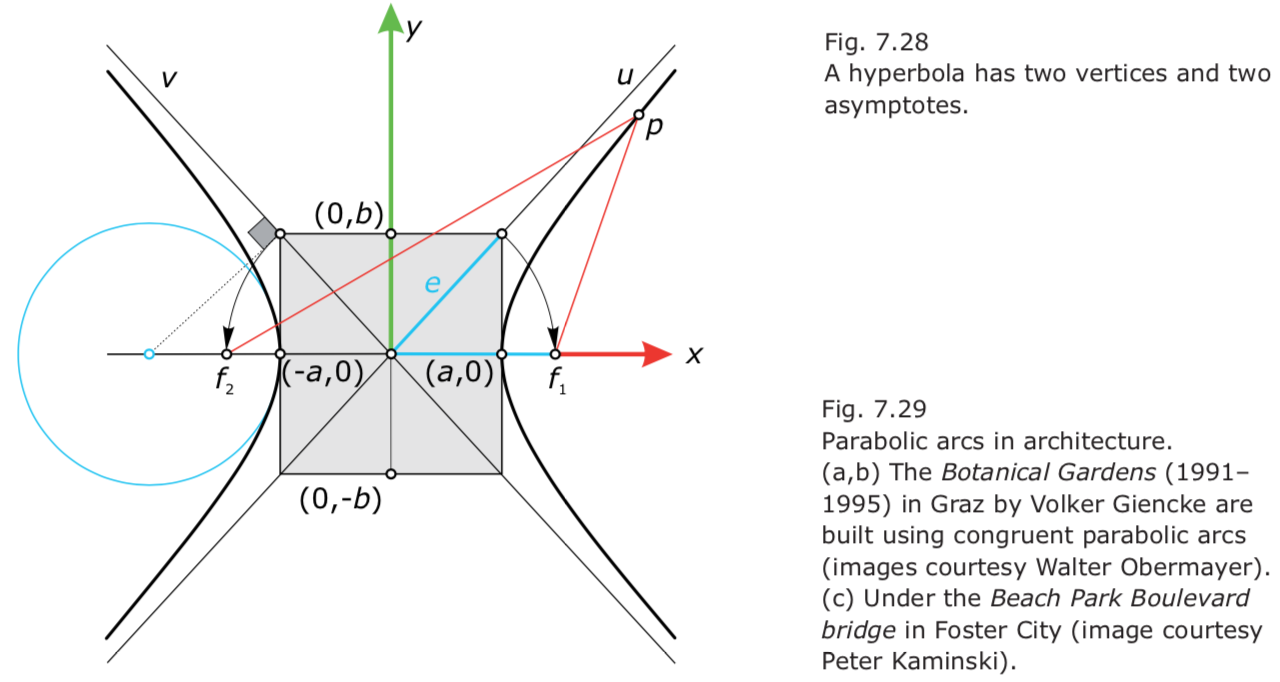
• parabola 抛物线：$x^2 – 2py = 0.$ 抛物线的evolute：

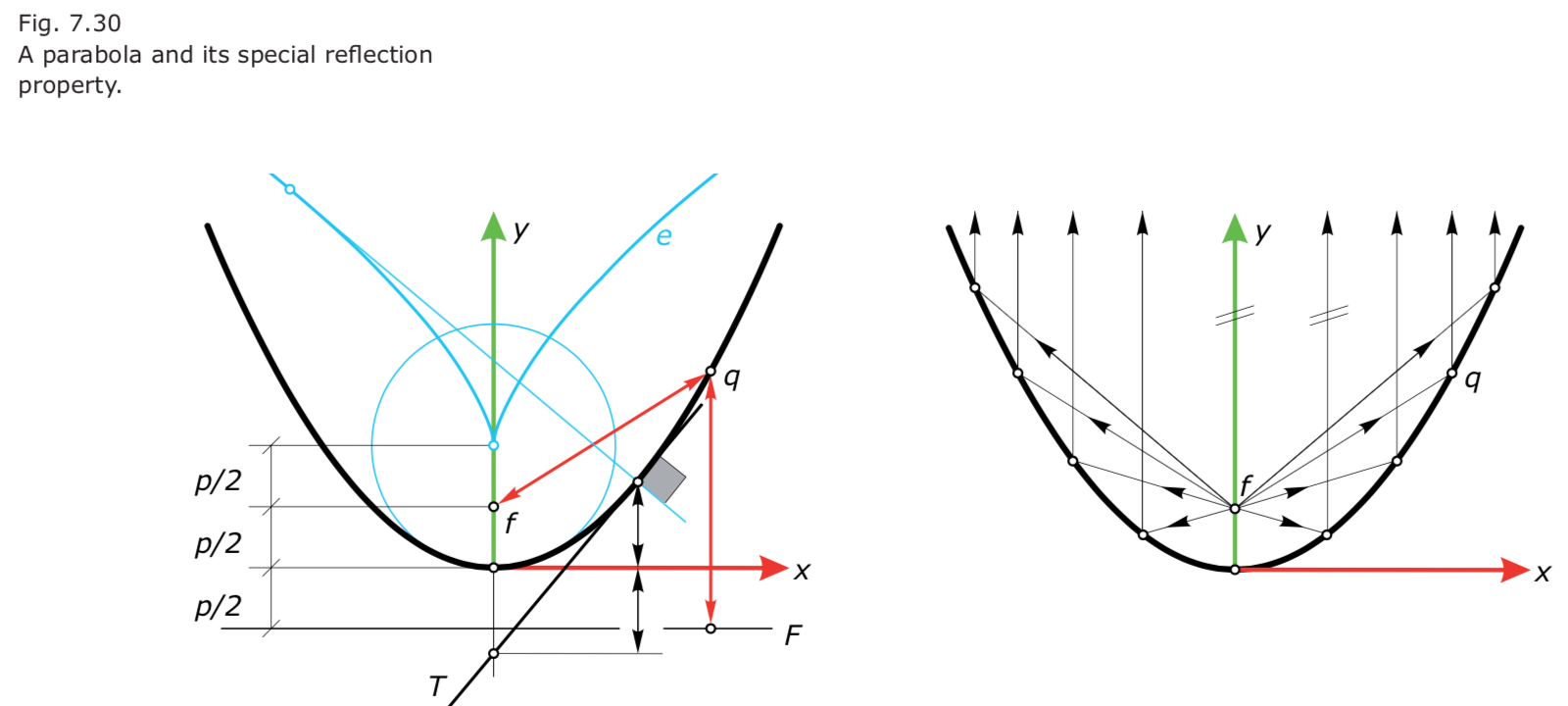
Surfaces 曲面

• 参数曲面：从平面区域投影到三维空间：
• 空间曲线切线生成的曲面：
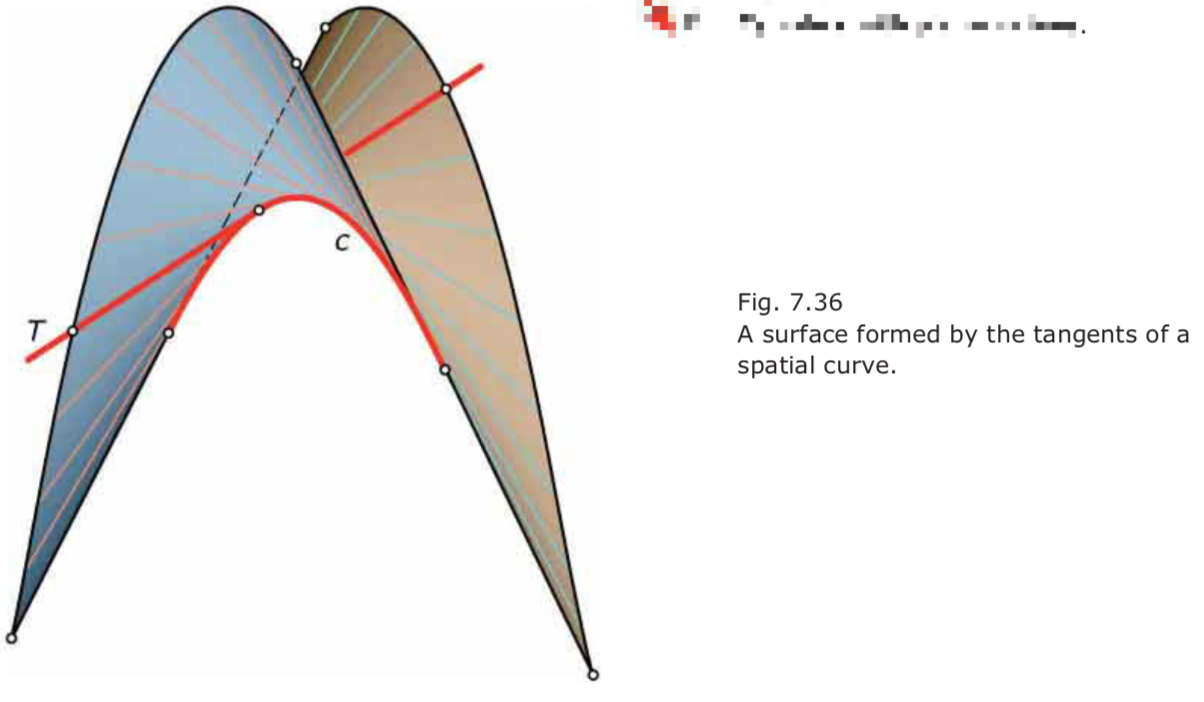
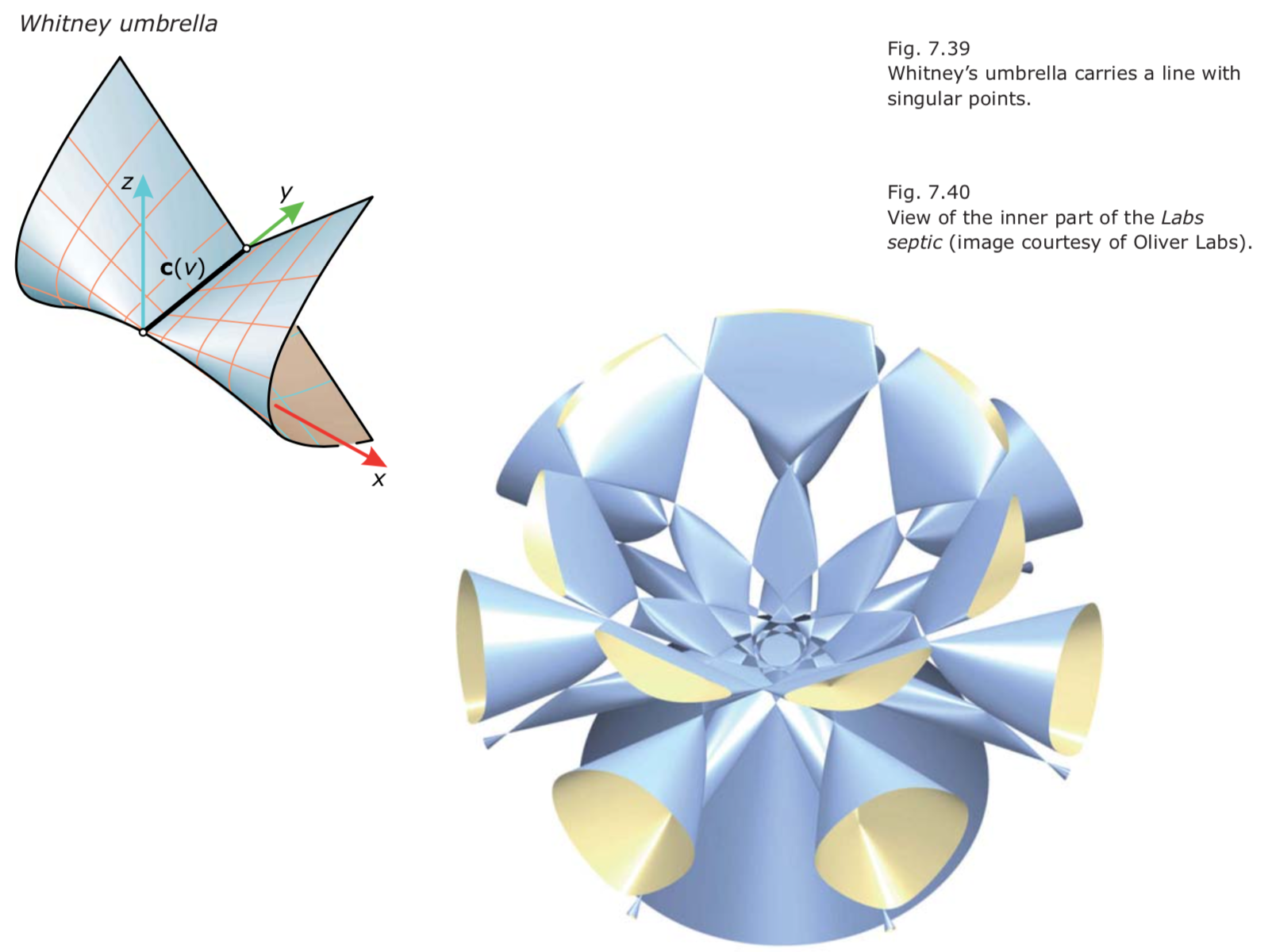
• Whitney’s umbrella： y轴正方向处有两个切平面，则上面的每个点都是奇异点； Labs septic 曲面含有99个奇异点：
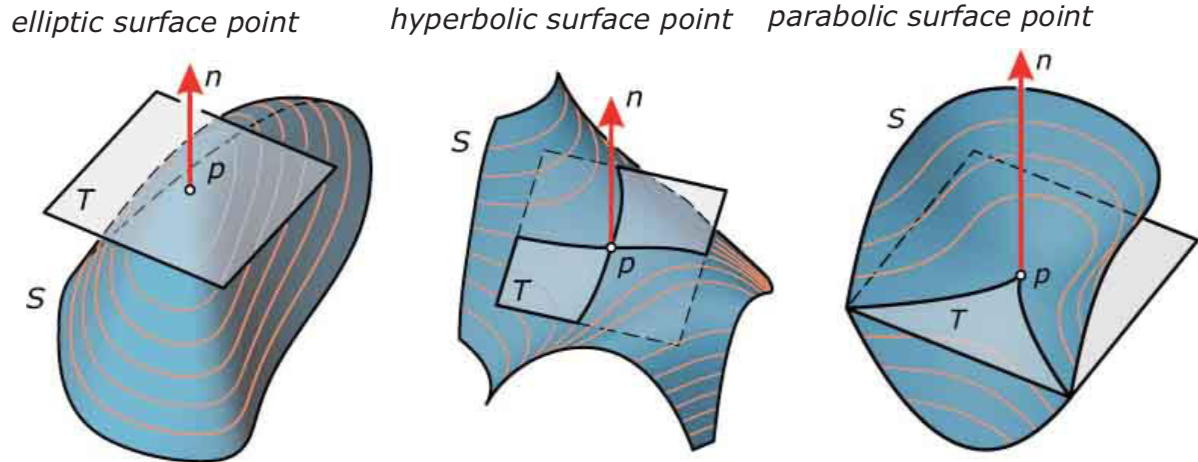
• 锥面点：elliptic surface point, hyperbolic surface point, parabolic surface point:

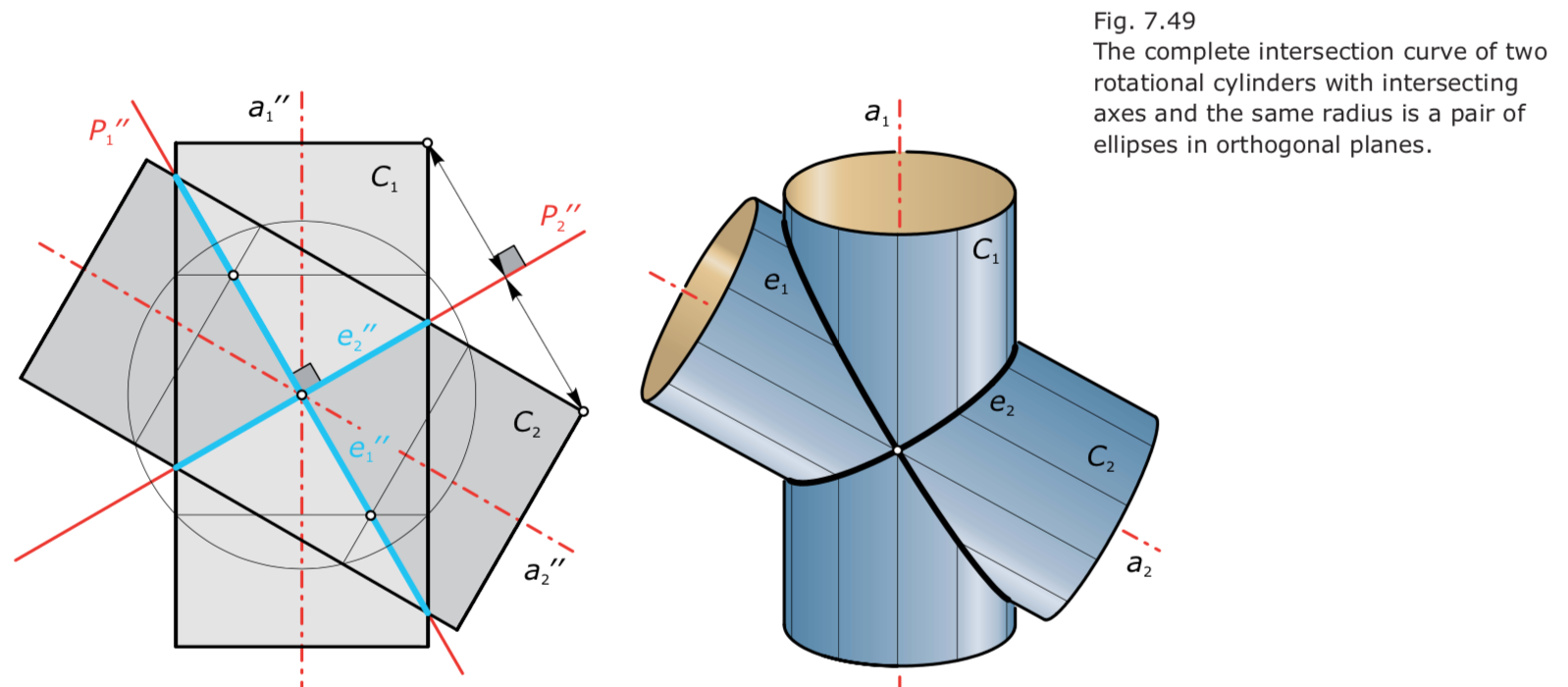
Intersection curves of surfaces 曲面的交线

• conic intersection 锥面相交形成的建筑vault穹顶：

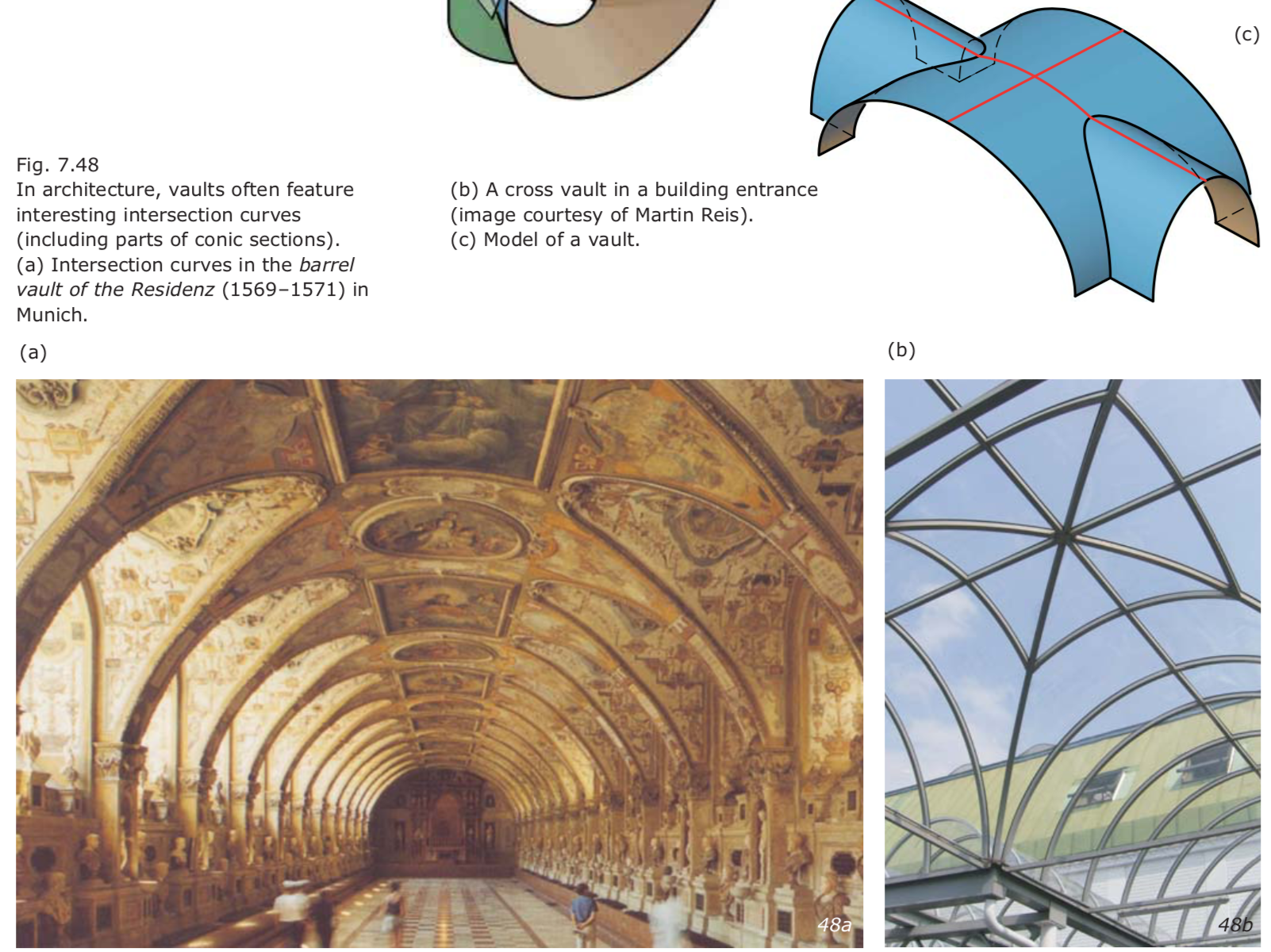
If two rotational cylinders or cones possess a common inscribed sphere, their intersection curve decomposes into a pair of conic sections or into a conic section and a single ruling.