Traditional surfaces classes 传统曲面类

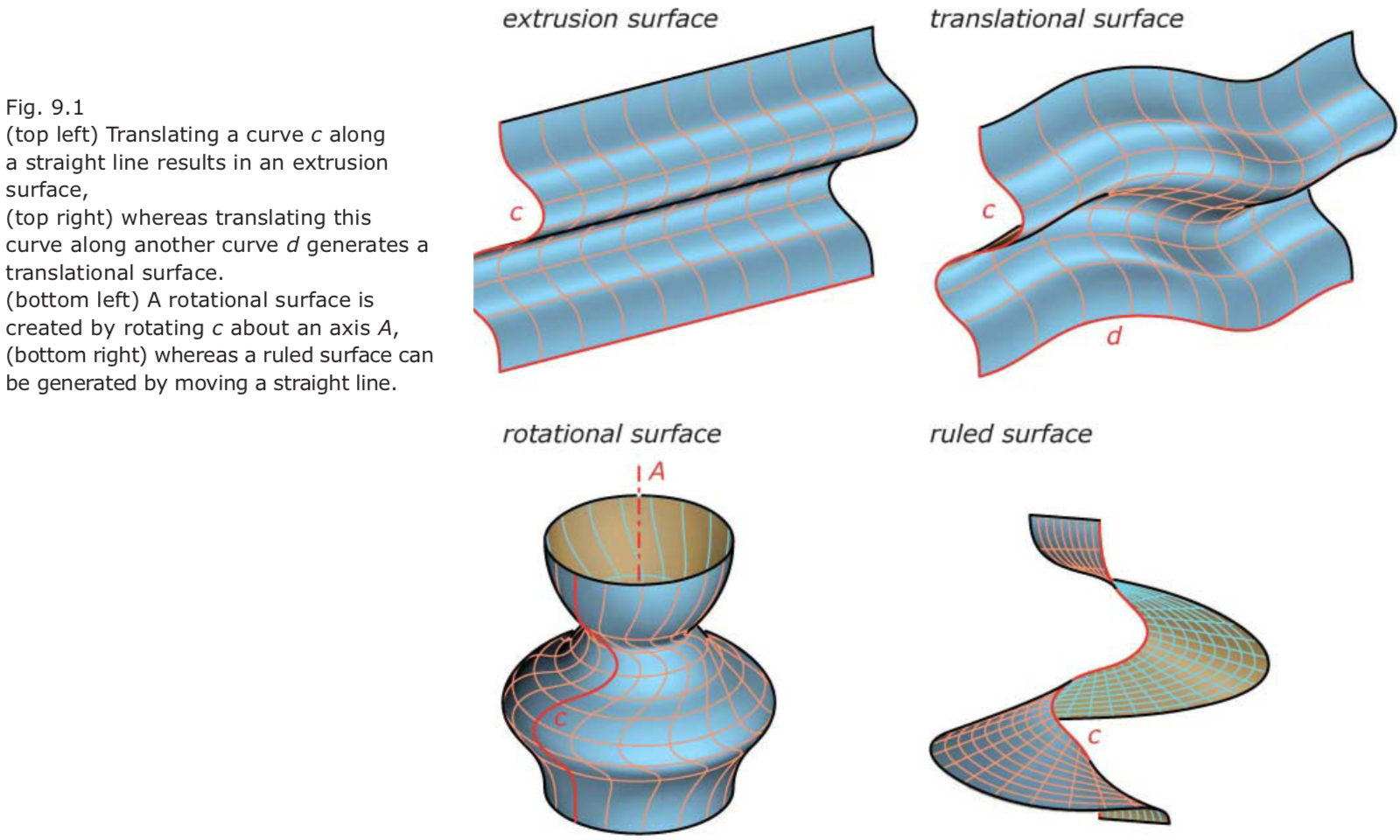
Rotational surfaces 旋转曲面

Mathematical description.

$x(u,v) = x(v)·cos u$,
$y(u,v) = x(v)·sin u$,
$z(u,v) = z(v).$
We call this the standard representation of a rotational surface.

Special rotational surfaces.

• A cylinder is generated when we rotate a straight line parallel to the axis.
• A straight line that intersects the rotational axis A generates a cone when we rotate it about A. The intersection point becomes the apex v of the cone.
• Rotating a circle c about any of its diameters produces a sphere.
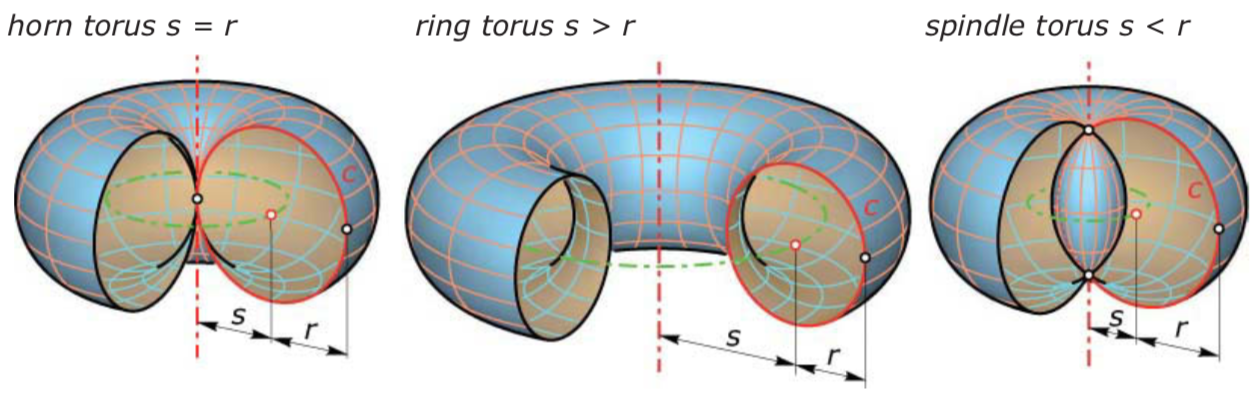
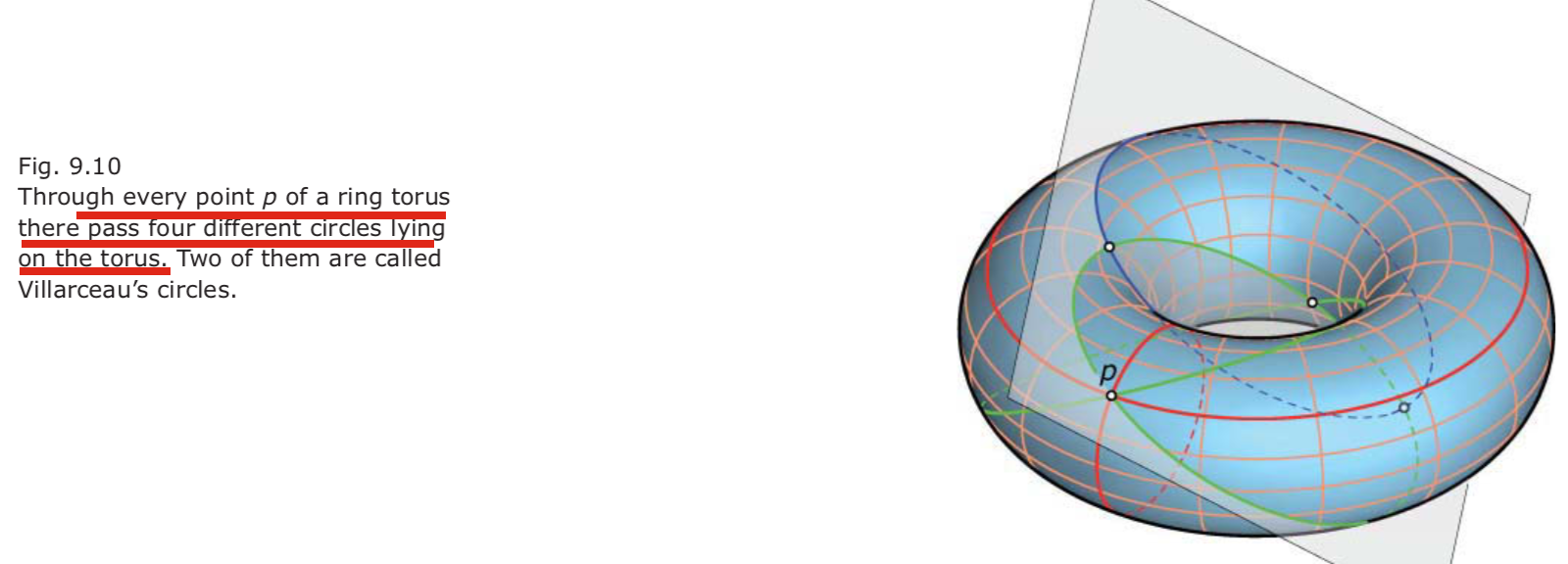
• We generate a torus by rotating a circle c about an arbitrary line. This straight line has to lie in the supporting plane of the circle c. Depending on the number of intersection points of c and the rotational axis, we obtain three different types of tori.
• Torus:
  x(u,v) = (s + r · cos v)·cos u,
  y(u,v) = (s + r · cos v)·sin u,
  z(u,v) = r · sin v.

Rotational quadrics.

• Oblate rotational ellipsoid: x2/a2 + y2/a2 + z2/c2 = 1 (a2 > c2)
• Prolate rotational ellipsoid: x2/a2 + y2/a2 + z2/c2 = 1 (a2 < c2)
• Two-sheet rotational hyperboloid: x2/a2 + y2/a2 – z2/c2 = –1
• One-sheet rotational hyperboloid: x2/a2 + y2/a2 – z2/c2 = +1
• Rotational paraboloid: z = a·(x2 + y2)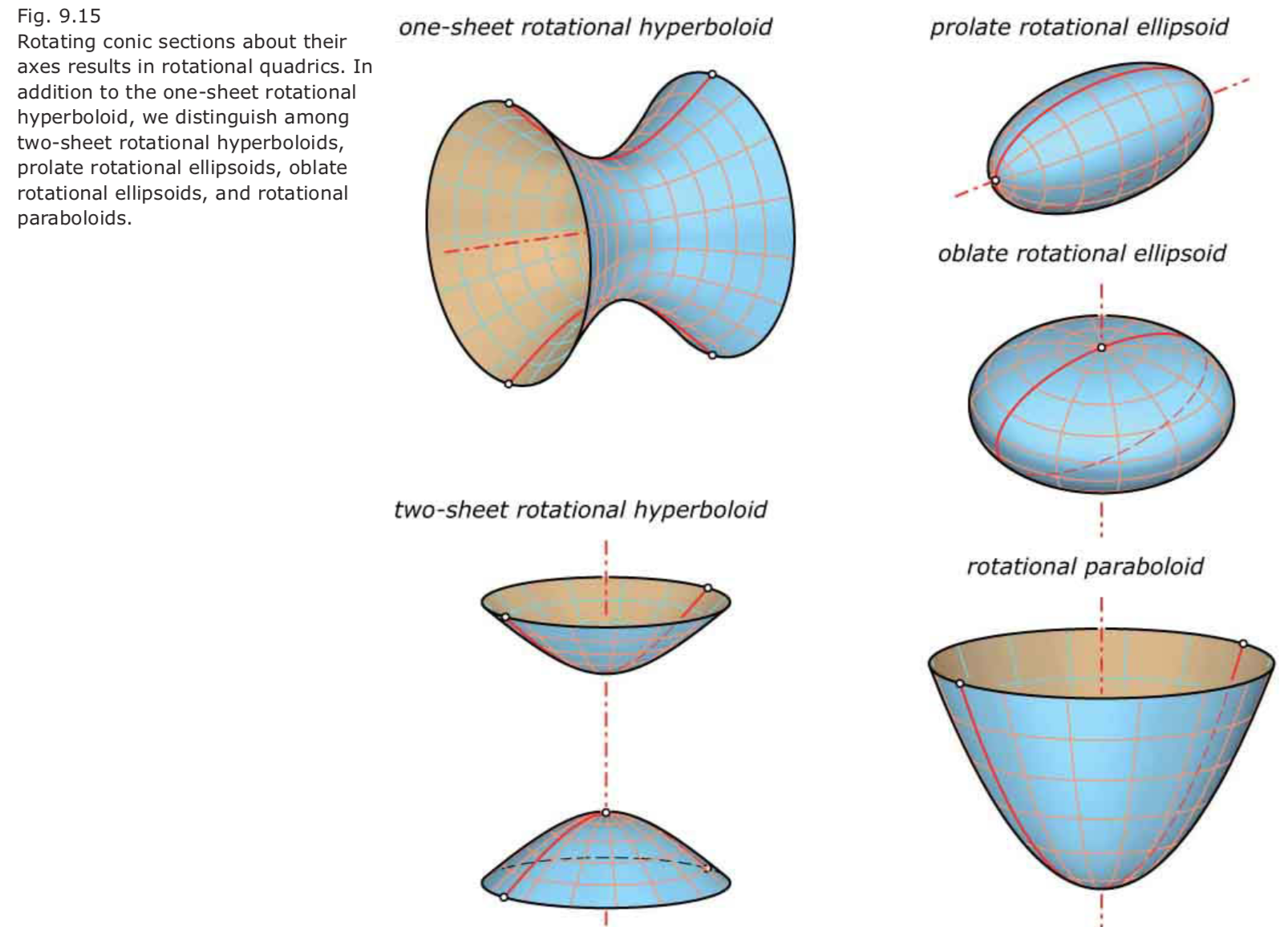

Translational surfaces 平移曲面

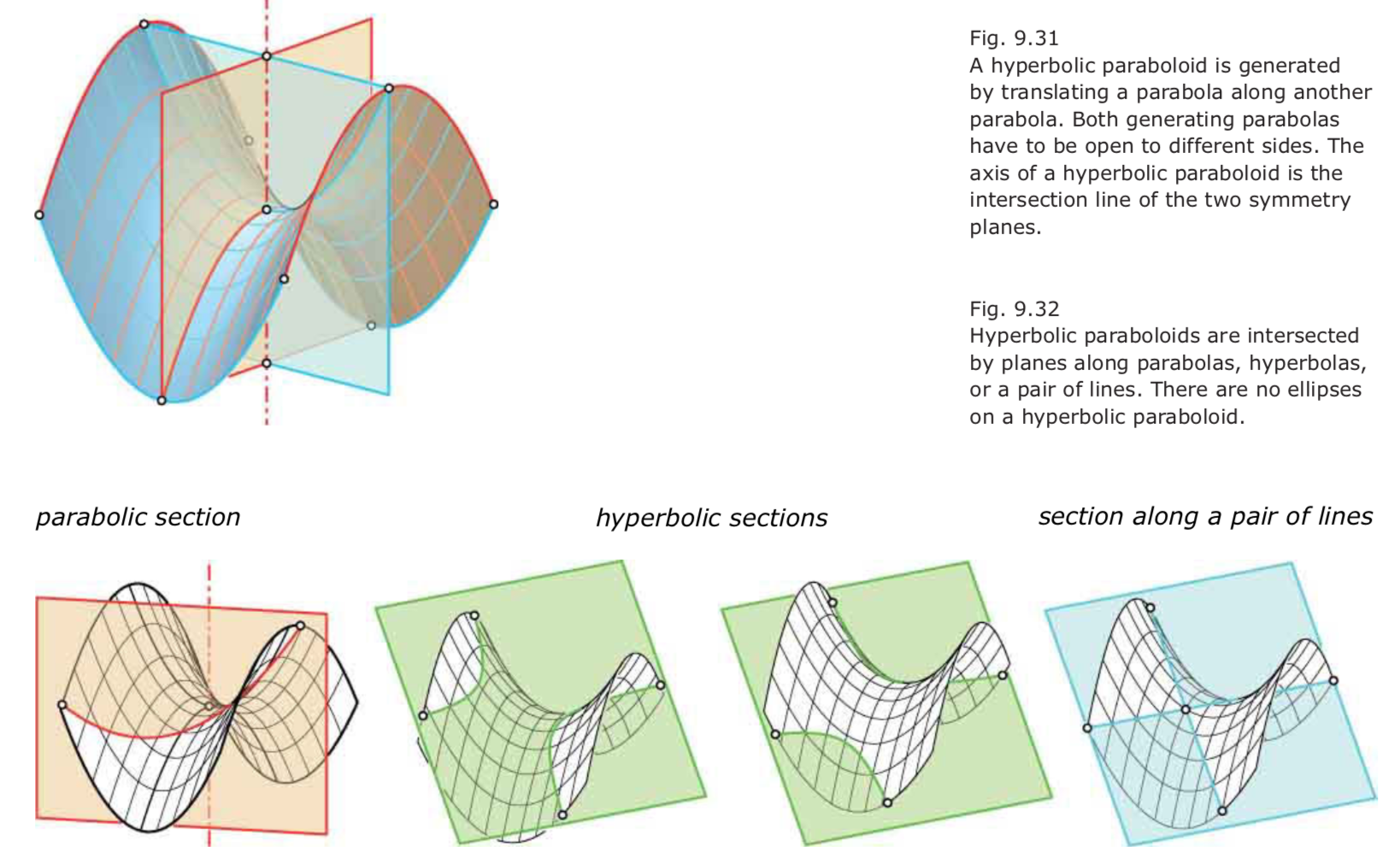
Hyperbolic paraboloid.

• A hyperbolic paraboloid carries exclusively hyperbolic points.
• Every part of this surface is saddle shaped.
• The fact that every tangent plane intersects the surface along a pair of different lines implies that the hyperbolic paraboloid carries two sets of lines.
• The hyperbolic paraboloid is another example of a ruled surface.
• The name of the hyperbolic paraboloid is sometimes shortened to HP surface.

Ruled surfaces 直纹面

• Cylinders, cones, one-sheet hyperboloids, and hyperbolic paraboloids are surfaces that carry families of straight lines.

• The class of all surfaces generated by a moving straight line are called ruled surfaces.

  

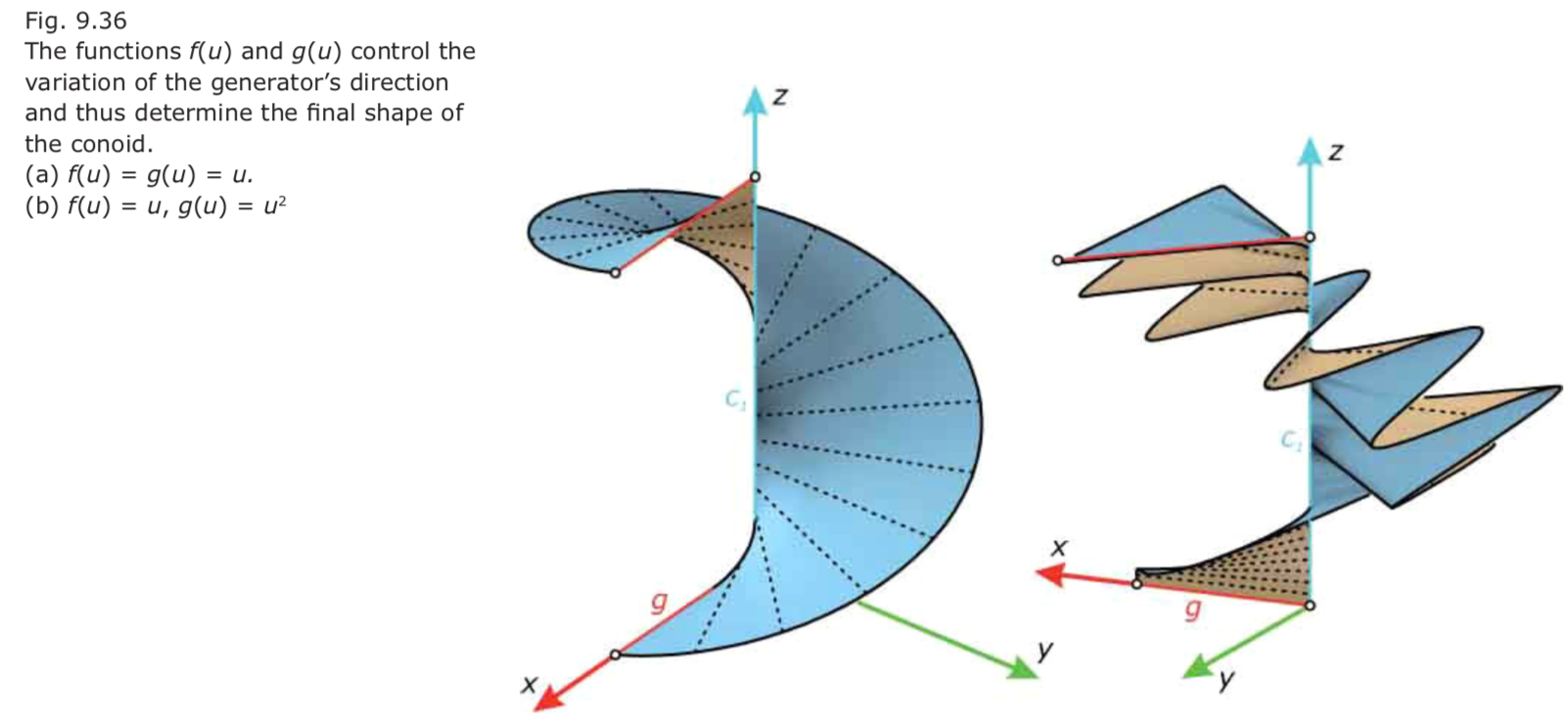
Conoid.

• Conoids can be generated by moving a straight line segment along a linear directrix c1.
  x(u,v) = v·cos(f(u)),
y(u,v) = v·sin(g(u)),
z(u,v) = u.
• For identical linear functions f(u) = g(u) = a⋅u + b common helicoids are generated.

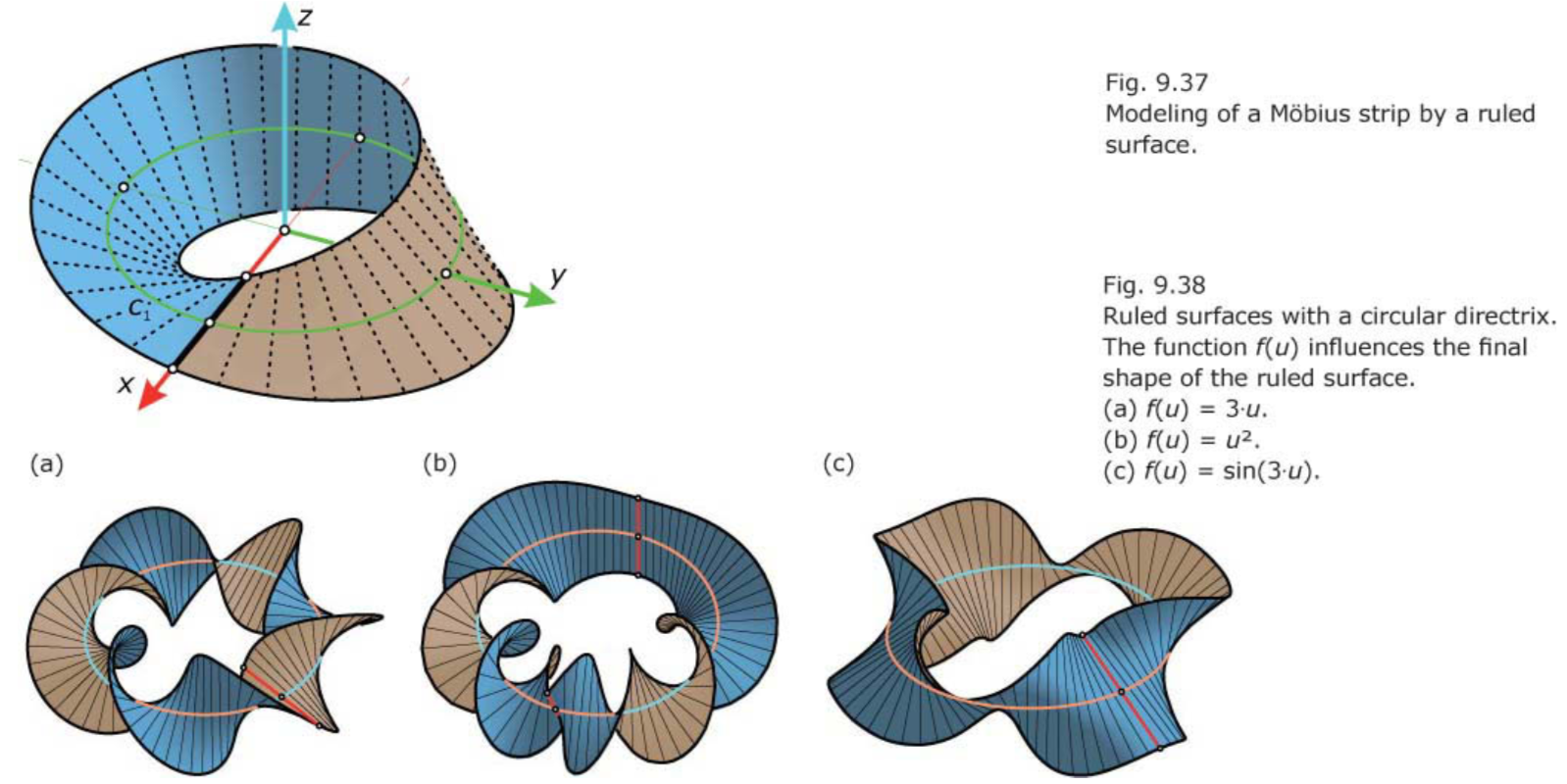
Möbius strip.

A parametric representation of a Möbius strip:
x(u,v) = r⋅cos(u) + v⋅cos(u/2)·cos(u),
y(u,v) = r⋅sin(u) + v⋅cos(u/2)·sin(u),
z(u,v) = v⋅sin(u/2).

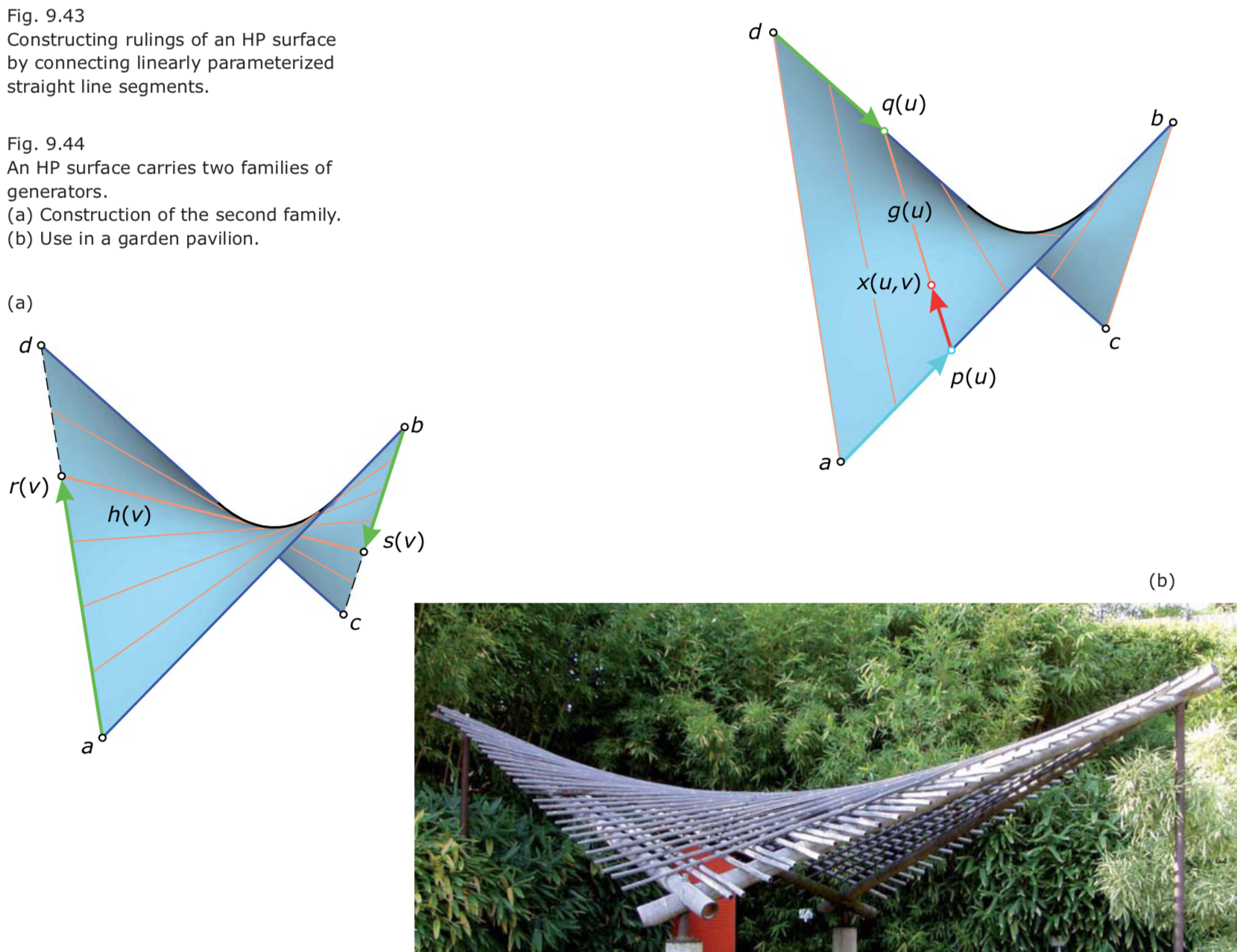
HP Surfaces.

• x = (1 – v)⋅p + v·q = (1 – v)·[(1 – u)·a + u·b] + v·[(1 – u)·d + u·c].
• x(u,v) = (1 – v)·(1 – u)·a + (1 – v)·u·b + v·(1 – u)·d + v·u·c.
• They are sometimes called double ruled surfaces.
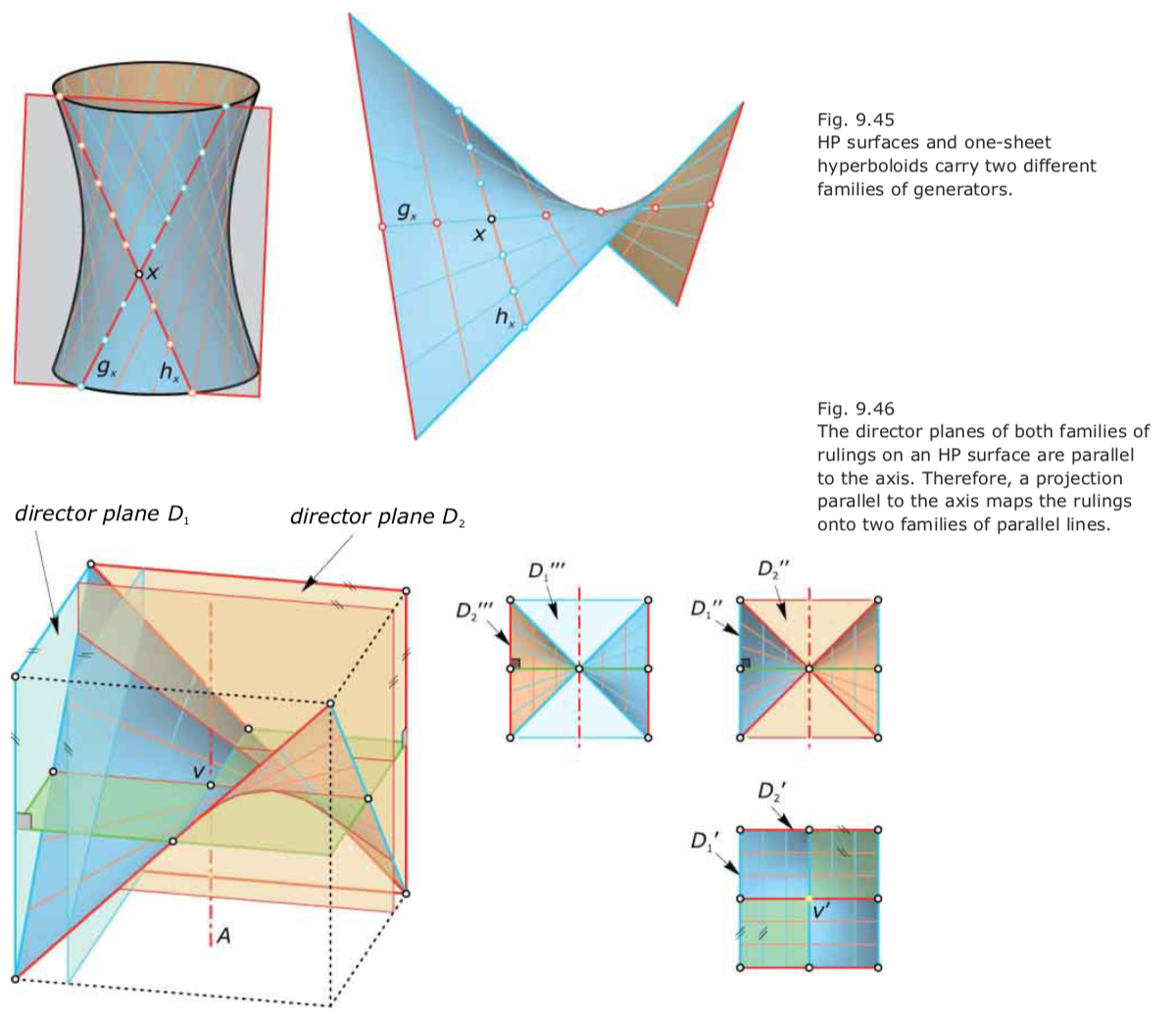
• The HP surfaces and the one-sheet hyperboloids are the only types of double ruled surfaces.
• In contrast to the one-sheet hyperboloid, all rulings of an HP surface that belong to the same family are parallel to a director plane.
• An HP surface has two different families of director planes according to the two families of rulings.

Plücker’s conoid.

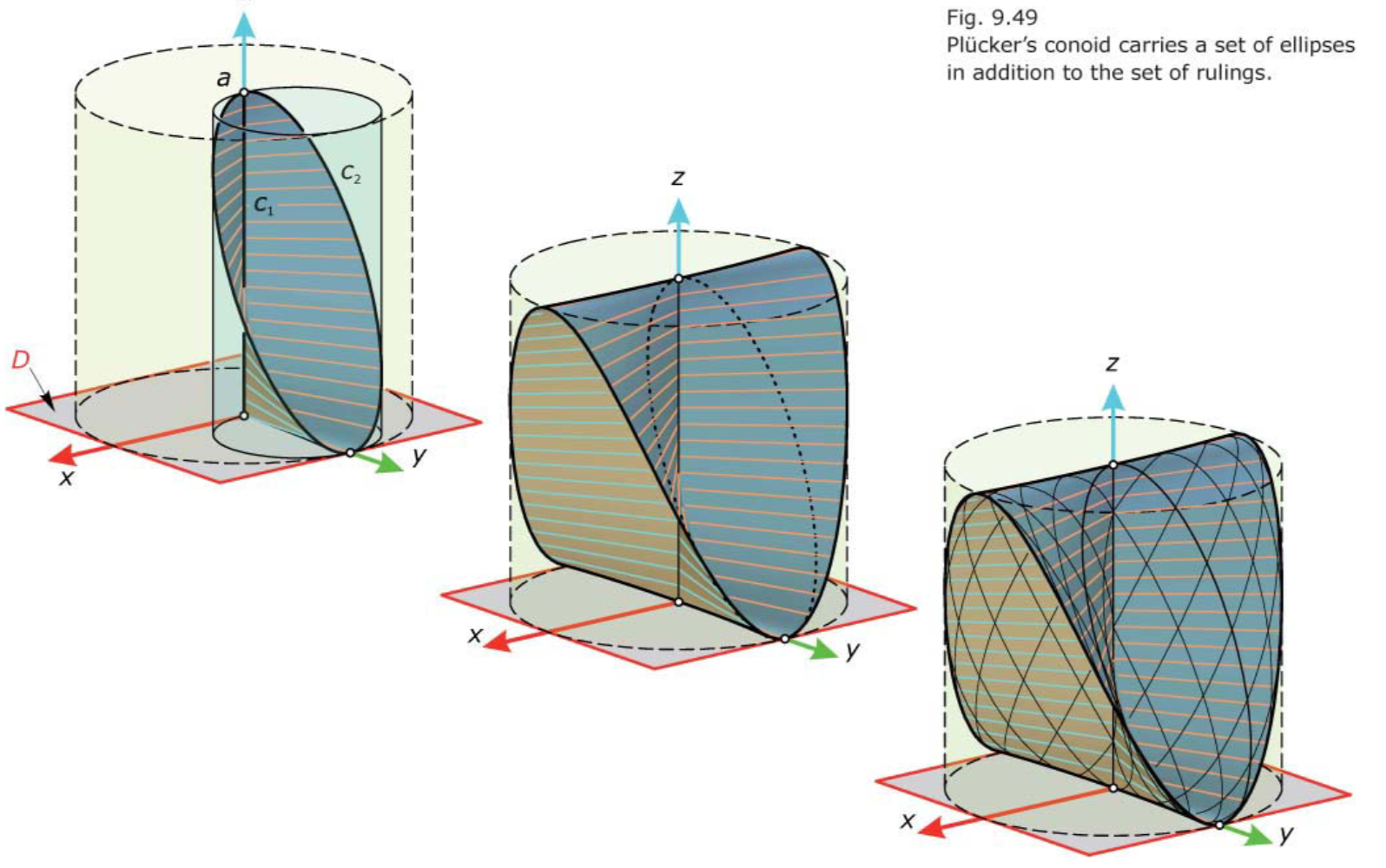
Tangent planes of ruled surfaces.

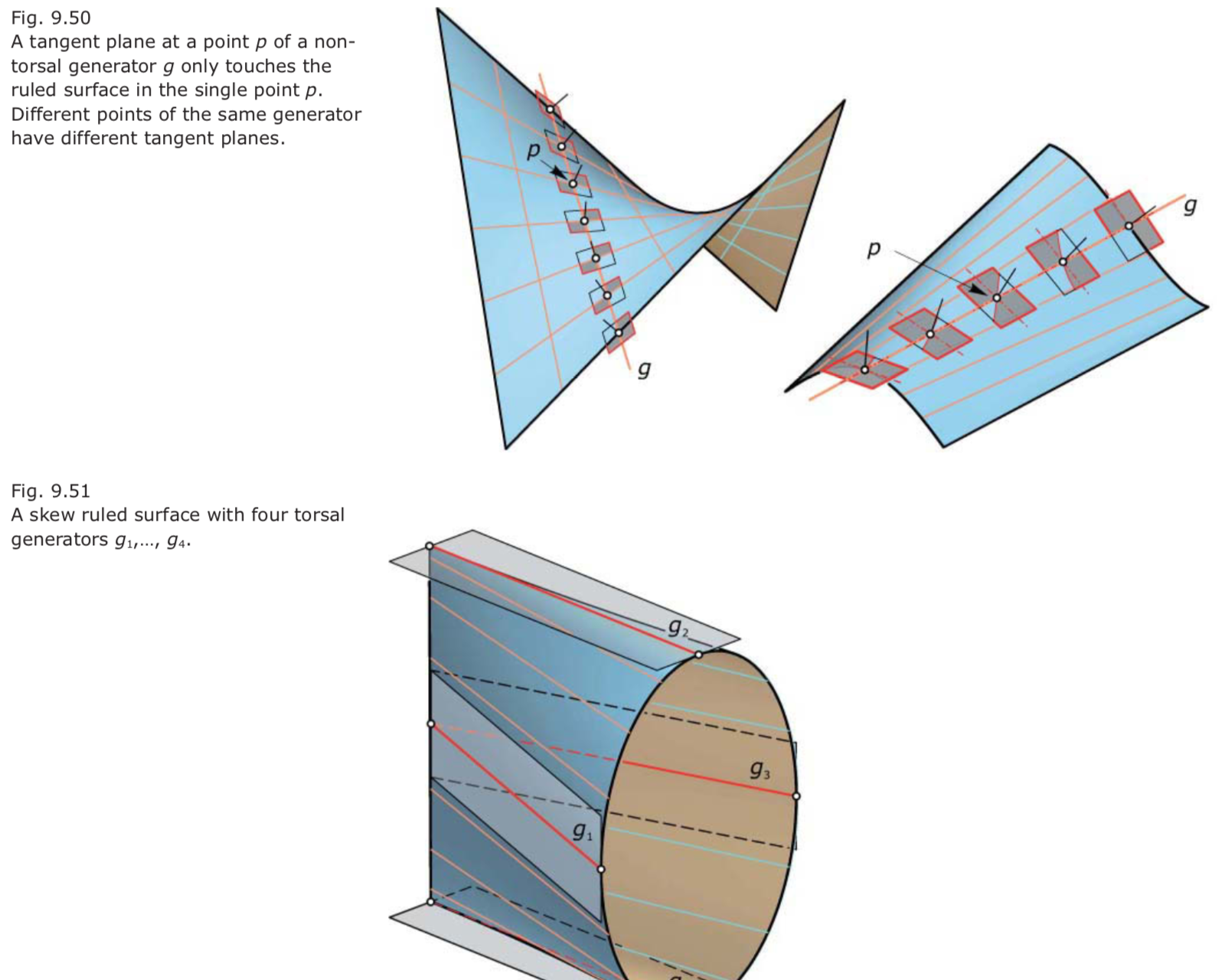
• Ruled surfaces (such as cylinders and cones) contain rulings where the tangent plane touches the surface along the entire line. Such rulings are called torsal generators, to distinguish them from the common case of the non-torsal generators:
• Ruled surfaces with exclusively torsal generators are called developable surfaces;
• Ruled surfaces consisting largely of non-torsal generators are called skew ruled surfaces (or warped ruled surfaces).
• Cylinders, cones, and ruled surfaces that consist of tangents of a spatial curve are developable surfaces.

Helical surfaces 螺旋面

Mathematical description

x(u,v) = x(v)·cosu,
y(u,v) = x(v)·sinu,
z(u,v) = z(v) + p·u.

Special helical surfaces.

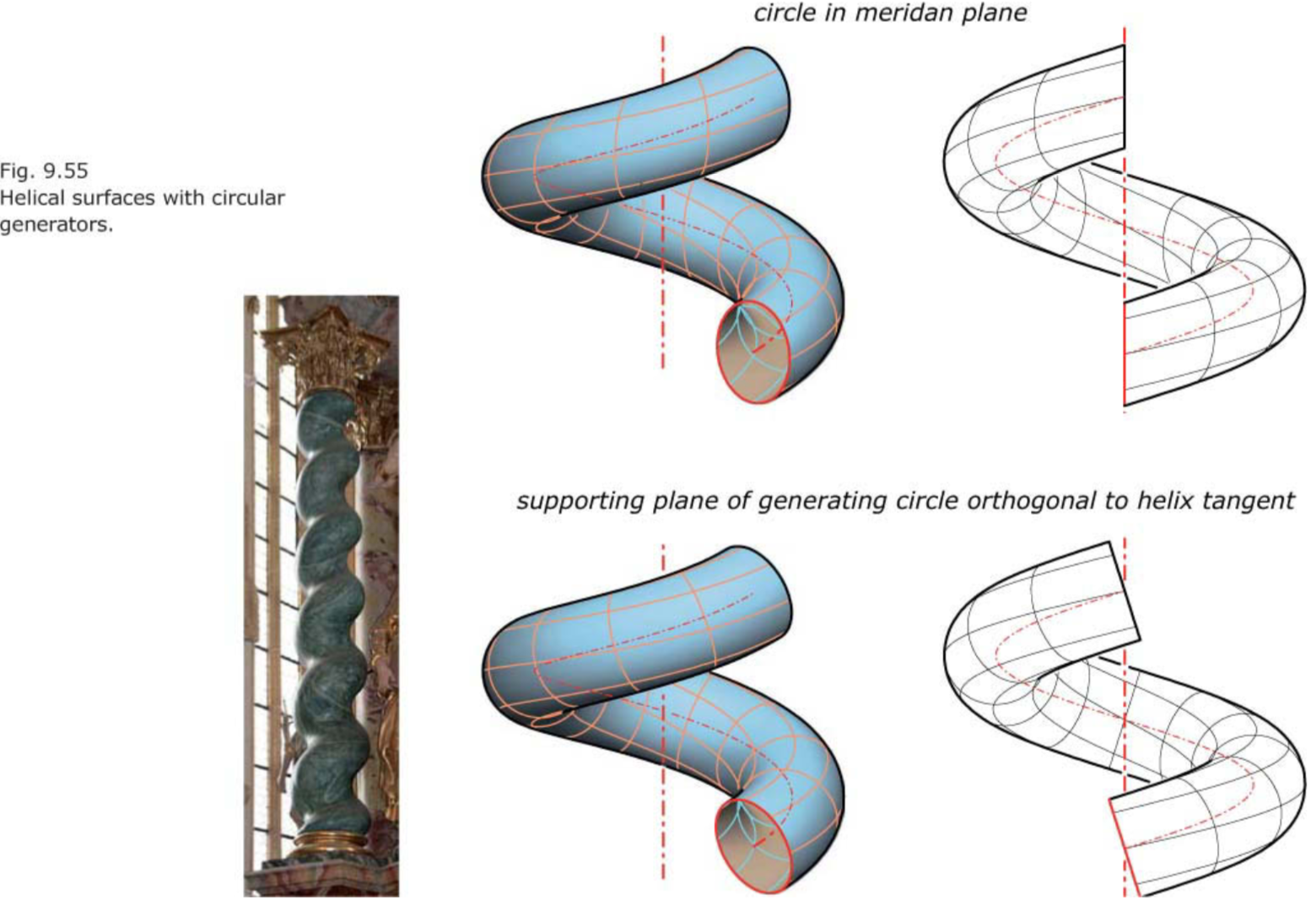
Among the helical surfaces, those with circles and straight lines as generators are commonly used for modeling purposes.

• A common helicoid is a helical surface whose generators orthogonally intersect the helical axis. 当gnerateor垂直螺旋轴时，得到的是螺旋面。
• A helicoid can be generated as a conoid. 螺旋面可以转化为悬链面。
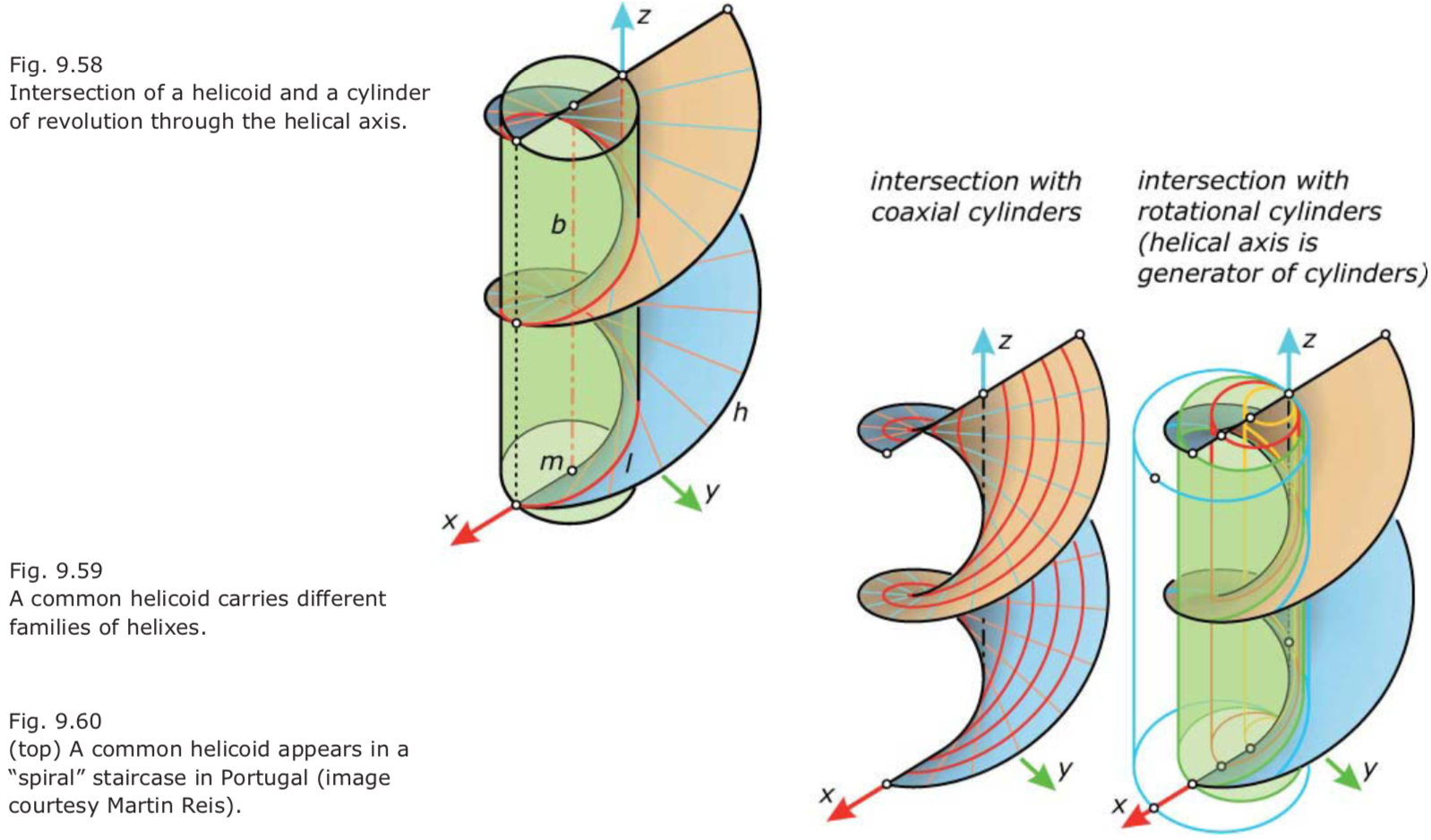
• Intersection of a helicoid and a cylinder of revolution through the helical axis.

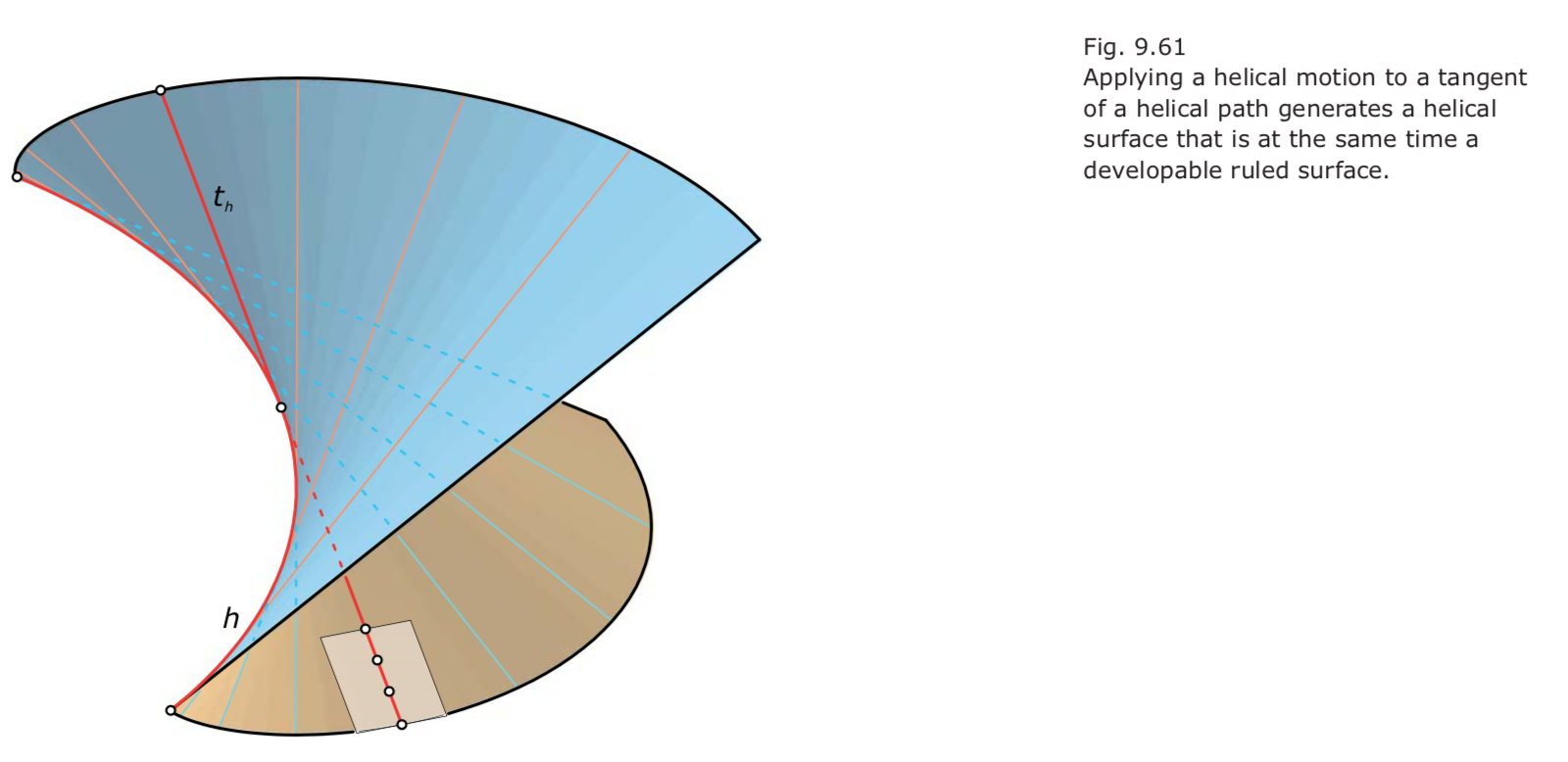
• Applying a helical motion to a tangent of a helical path generates a helical surface that is at the same time a developable ruled surface. 旋转的曲面的切向量也构成旋转面，且是个可展曲面。
• The helix h is a singular curve of the surface and creates a sharp edge on it. 该旋转曲面的螺旋轴是奇异线，产生了尖边。
• As is typical of developable ruled surfaces, every tangent plane touches along the entire generator $t_h$. generator 是 torsal的。

Pipe surfaces 管面

A pipe surface is the envelope of spheres of equal radius r whose centers lie on a curve c, called the spine curve or central curve c.