Freeform surfaces 自由形曲面


Bezier Surfaces
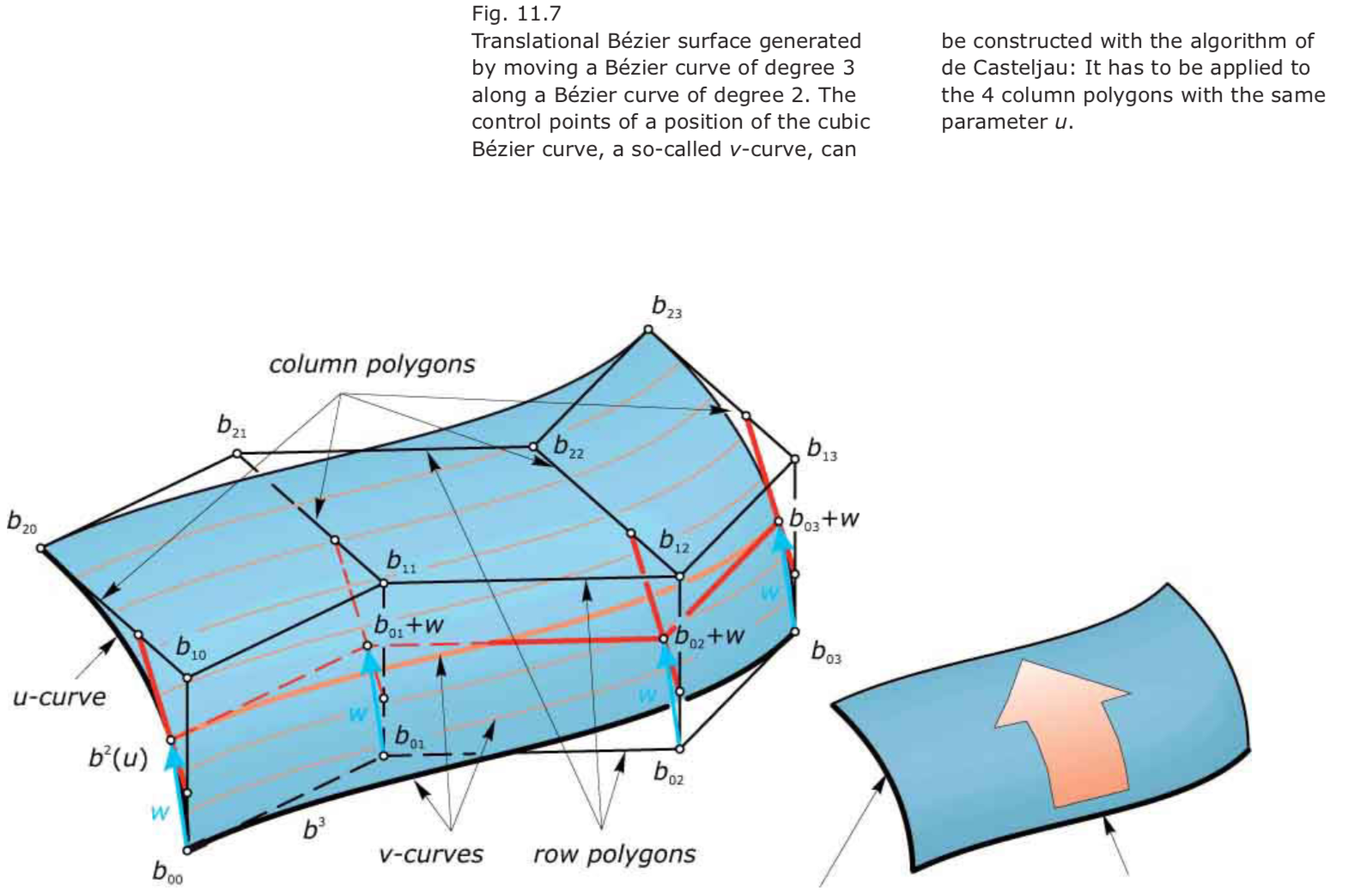
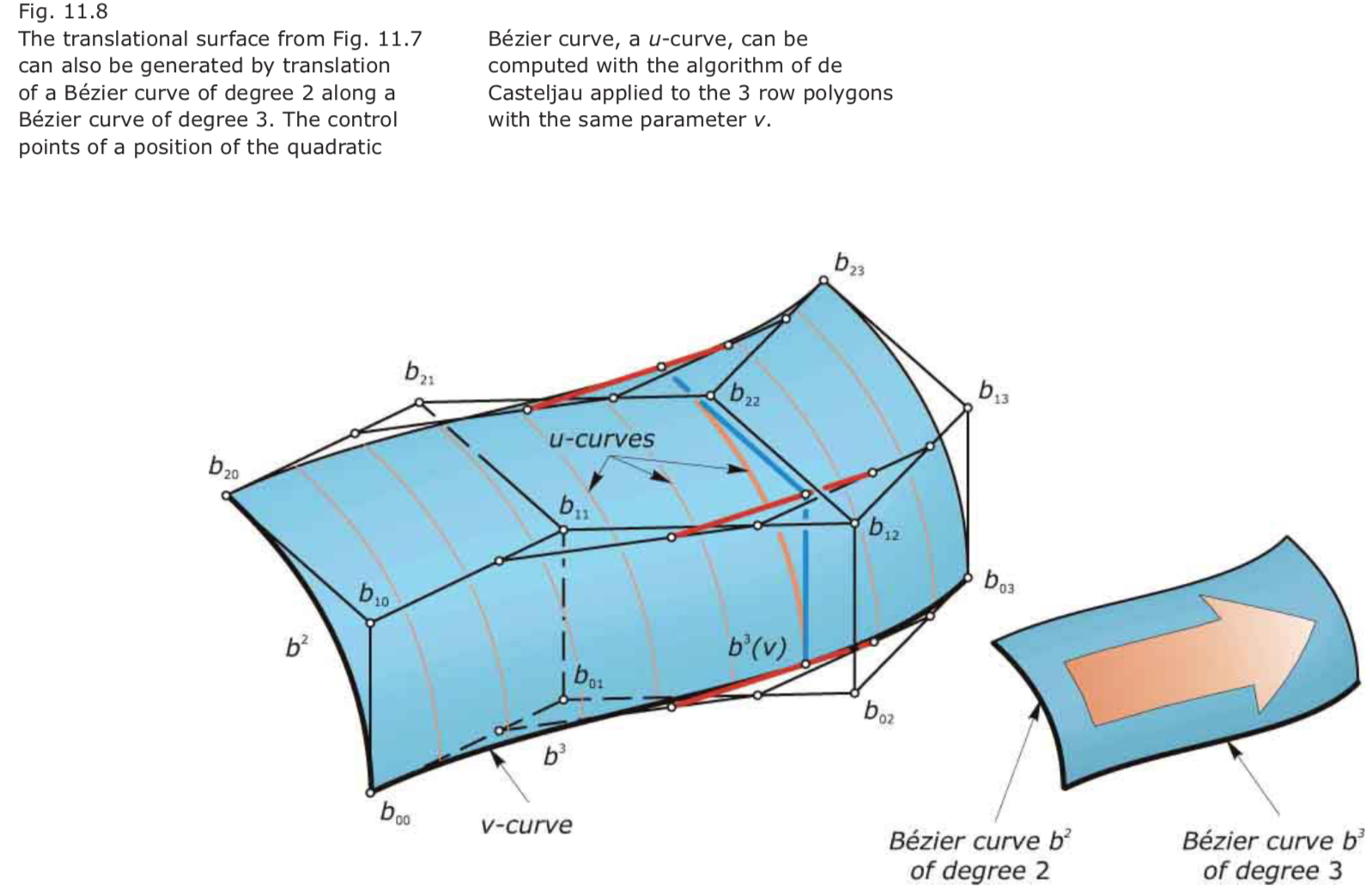
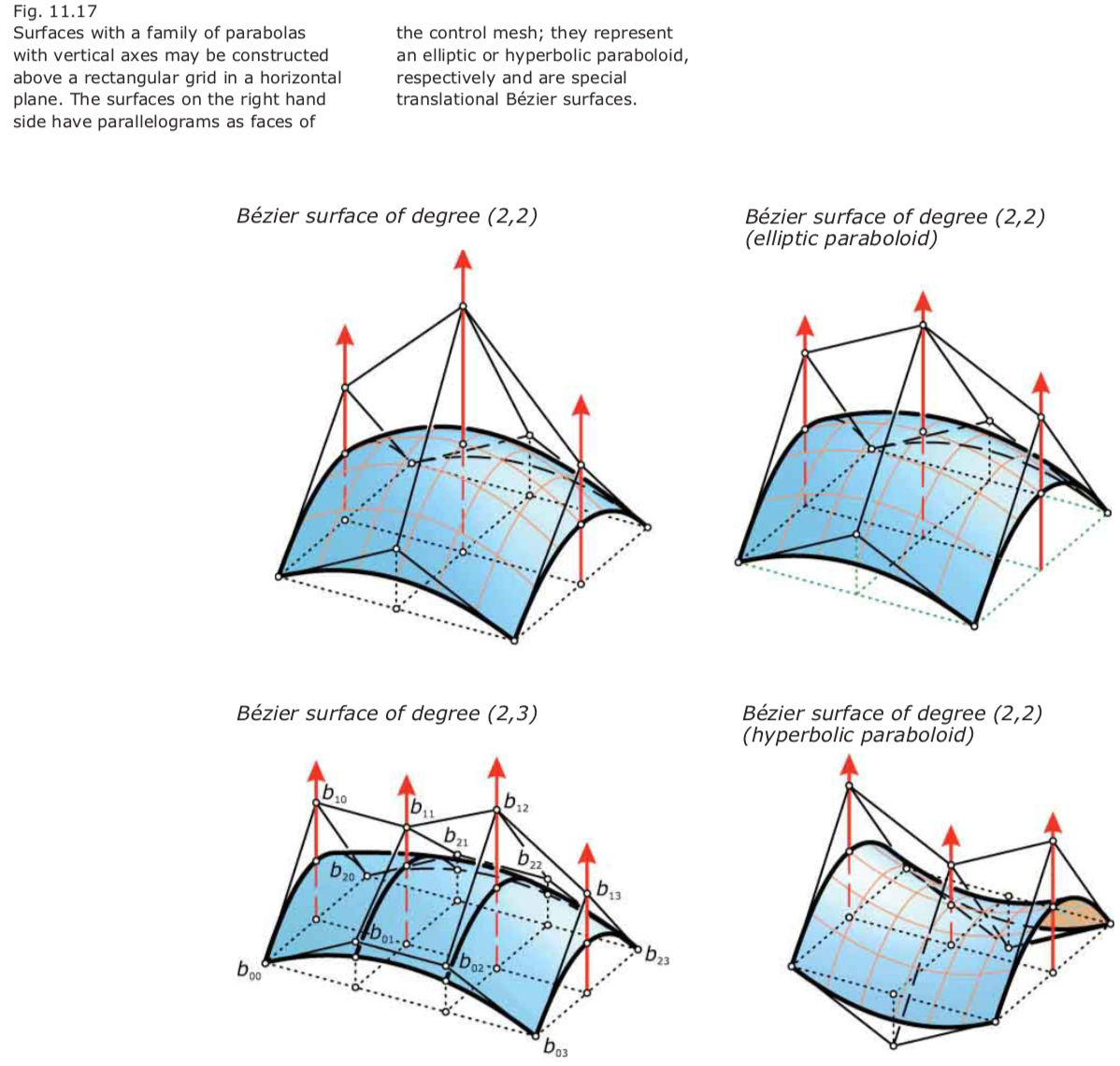
Translational Bézier surfaces:
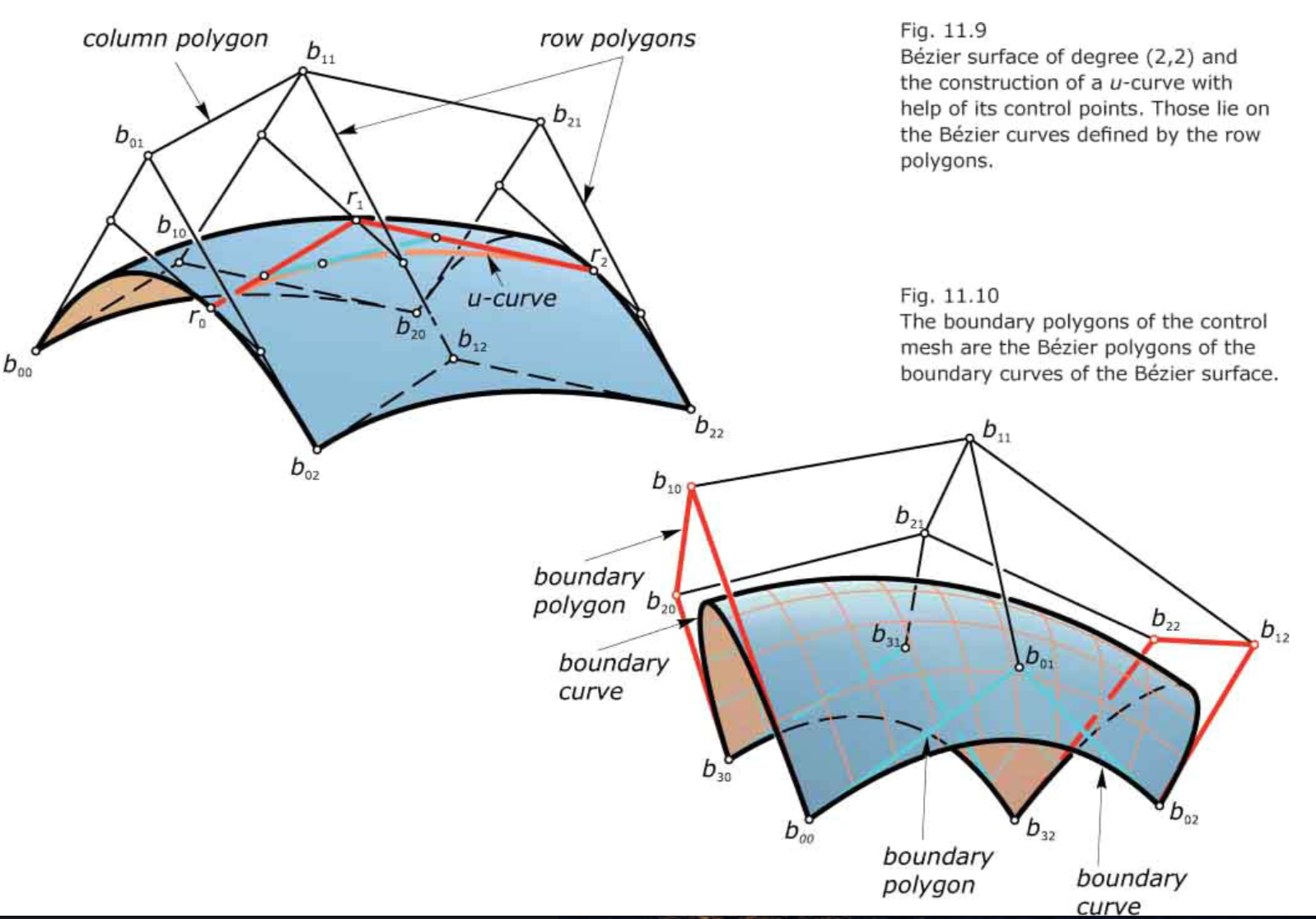
- Each boundary polygon of the control mesh defines a Bézier curve that is a boundary curve of the designed Bézier surface patch. Bezier曲面的边界是Bezier曲线.
- The boundary polygons are the only row and column polygons that define curves on the surface. 内部控制多边形生成的Bezier曲线,不一定在曲面上,除非是translational bezier 曲面:
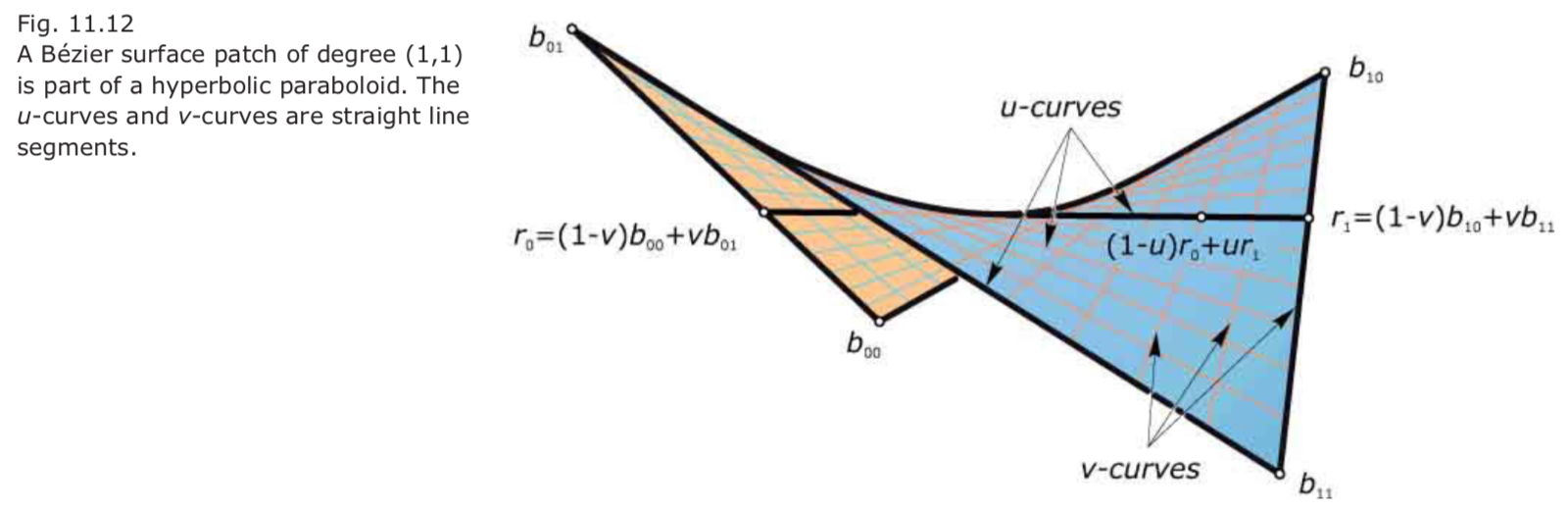
Bézier surfaces of degree (1,1):
- $r_0 = (1 – v)b_{00} + v b_{01} $
- $r_1 = (1 – v)b_{10} + vb_{11}$
- $b(u,v) = (1 – u)(1 – v)b_{00} + (1 – u)vb_{01} + u(1 – v)b_{10} + uvb_{11}$
- This shows that the surface is (part of ) a hyperbolic paraboloid (or part of a plane if the control quad is planar).
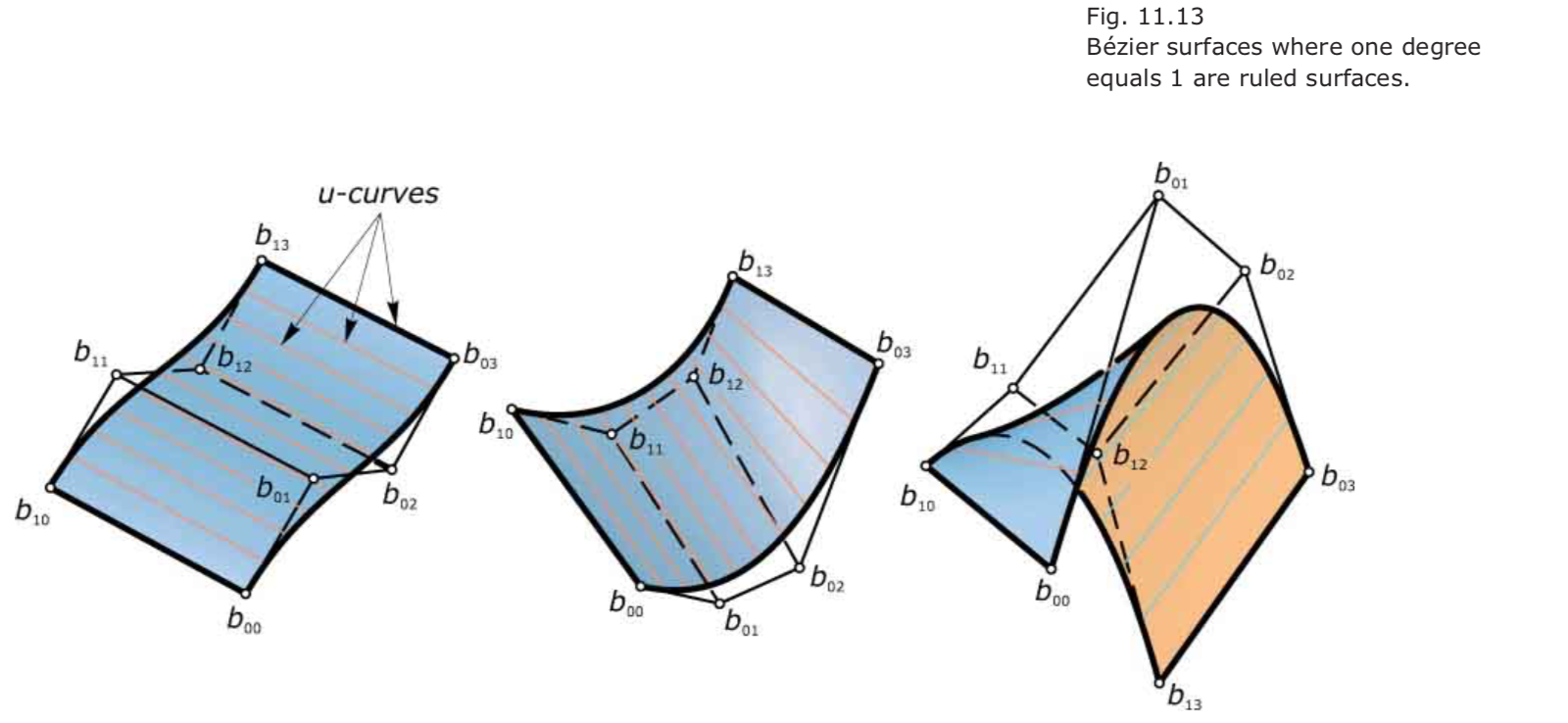
Bézier surfaces that are also ruled surfaces:
Consider a Bézier surface of degree $(1,n)$. Its u-curves are Bézier curves of degree 1 and therefore straight line segments. Therefore, this surface is a ruled surface—spanning two Bézier curves of degree $n$.
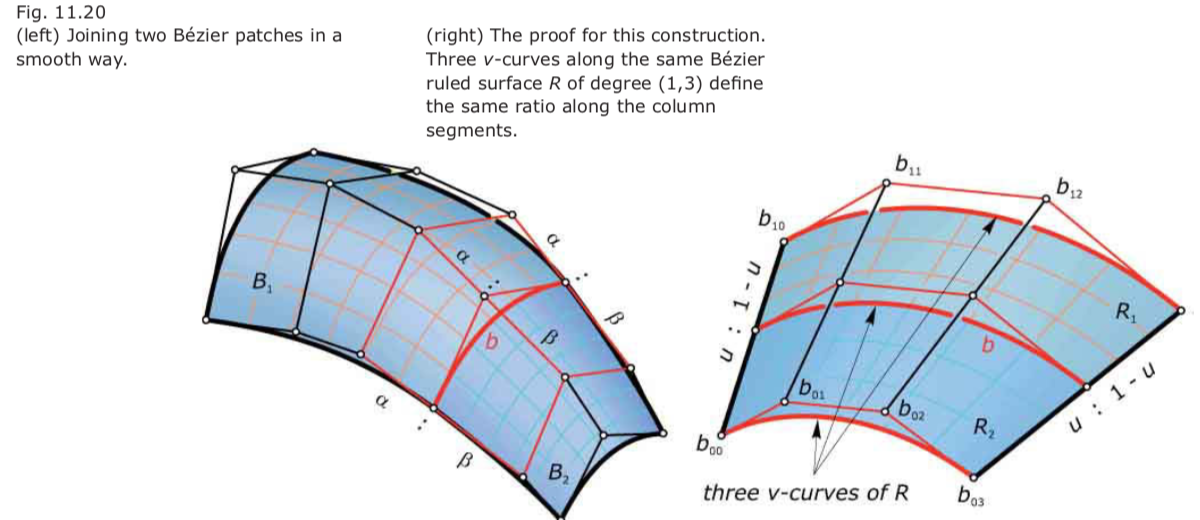
Bézier surfaces joined smoothly:
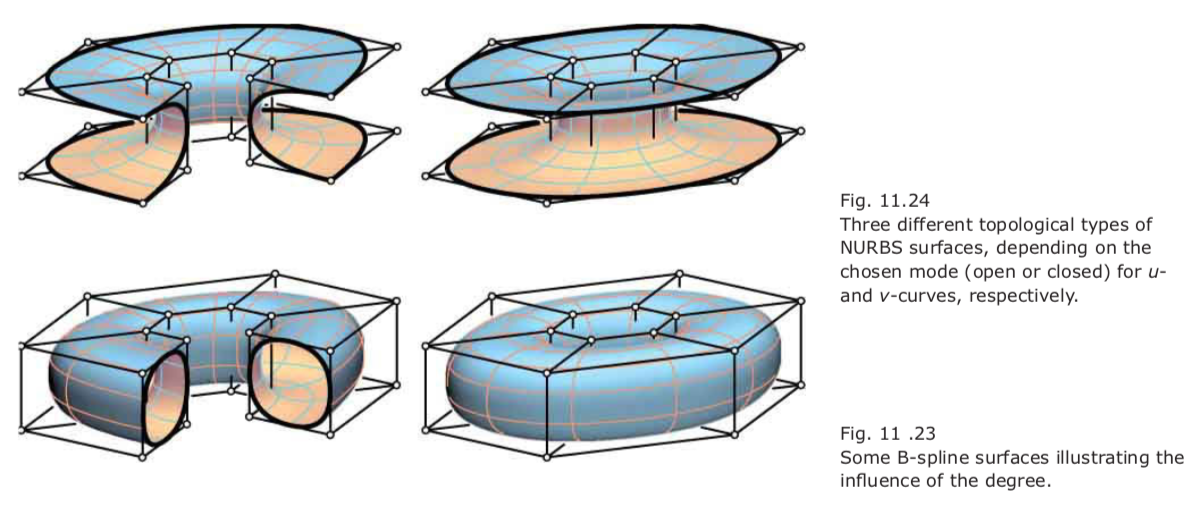
B-spline surfaces and NURBS Surfaces
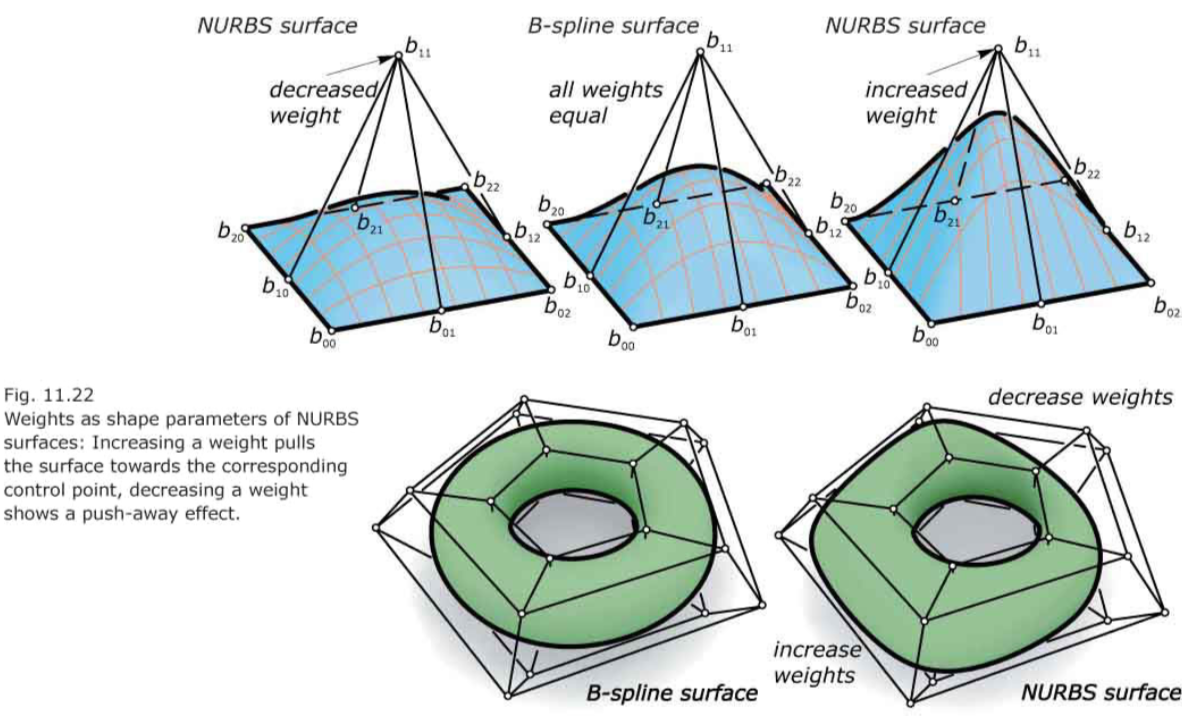
- Open mode for u- and v-curves: the surface is a four-sided patch.
- Closed mode in one direction (u or v), open mode in the other direction: such a surface looks like a deformed piece of a pipe.
- Closed mode in both directions: the surface looks like a deformed torus.
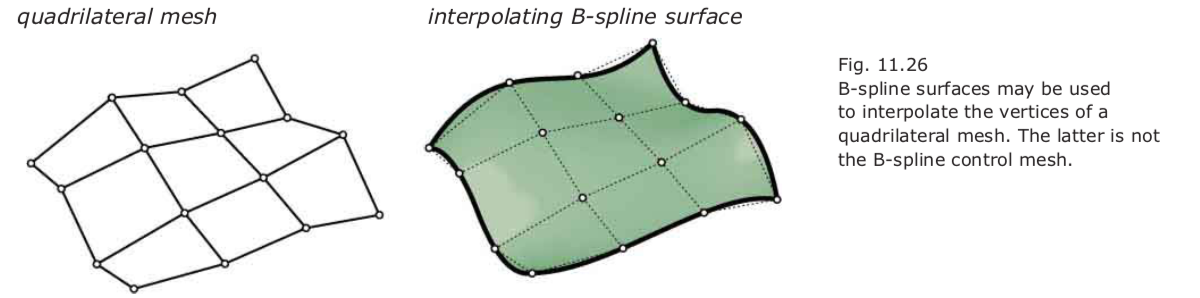
Interpolating spline surfaces:
This interpolation problem in its most general form is difficult to solve. However, the following solution is easy and is implemented in most 3D modelers: Given a set of points, arranged like the control points in a quadrilateral mesh, pass a B-spline surface through it.
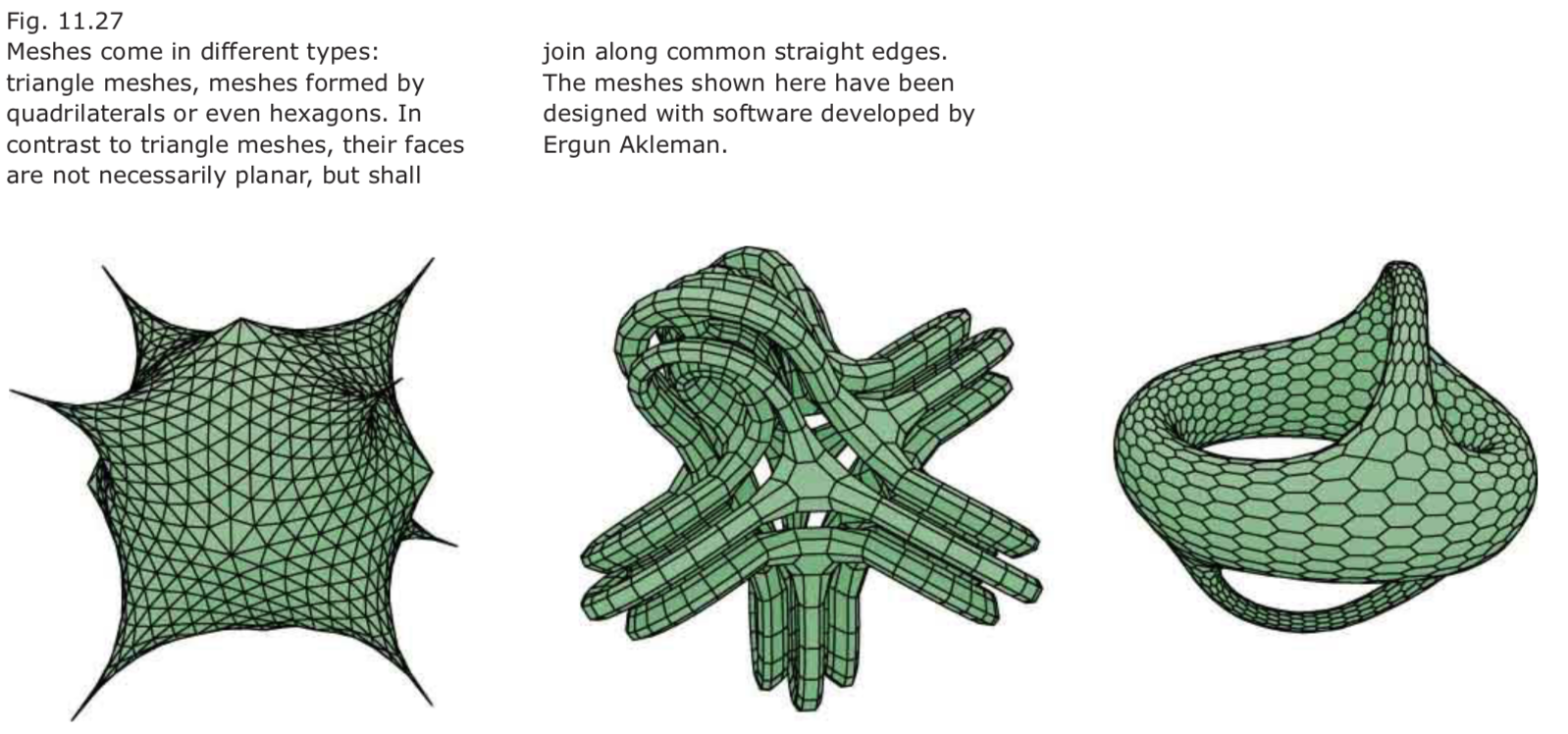
Meshes

- Roughly speaking, a mesh is a collection of points (vertices) arranged into basic elements called faces.
- The faces are bounded by polygons. Typically, one type of polygon dominates (e.g., triangle, quadrilateral, or even hexagon).
Geometry and connectivity:
- first discuss their connectivity—also refered to as their “mesh topology.”
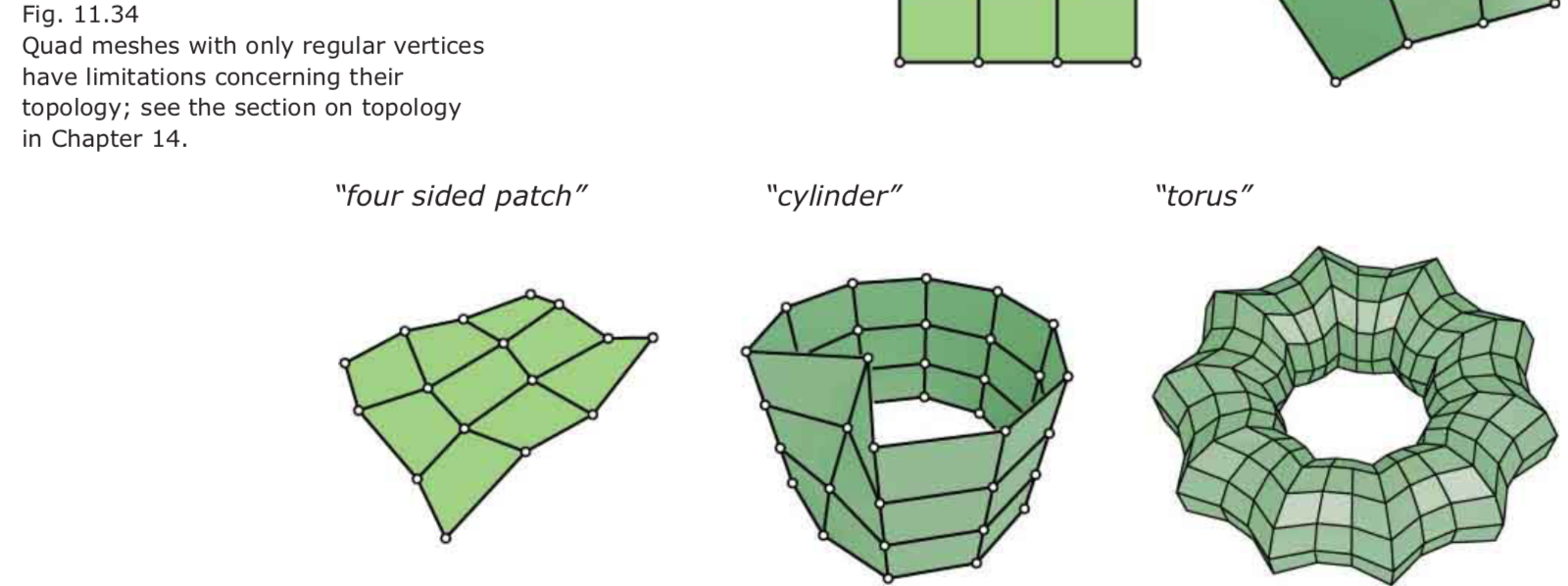
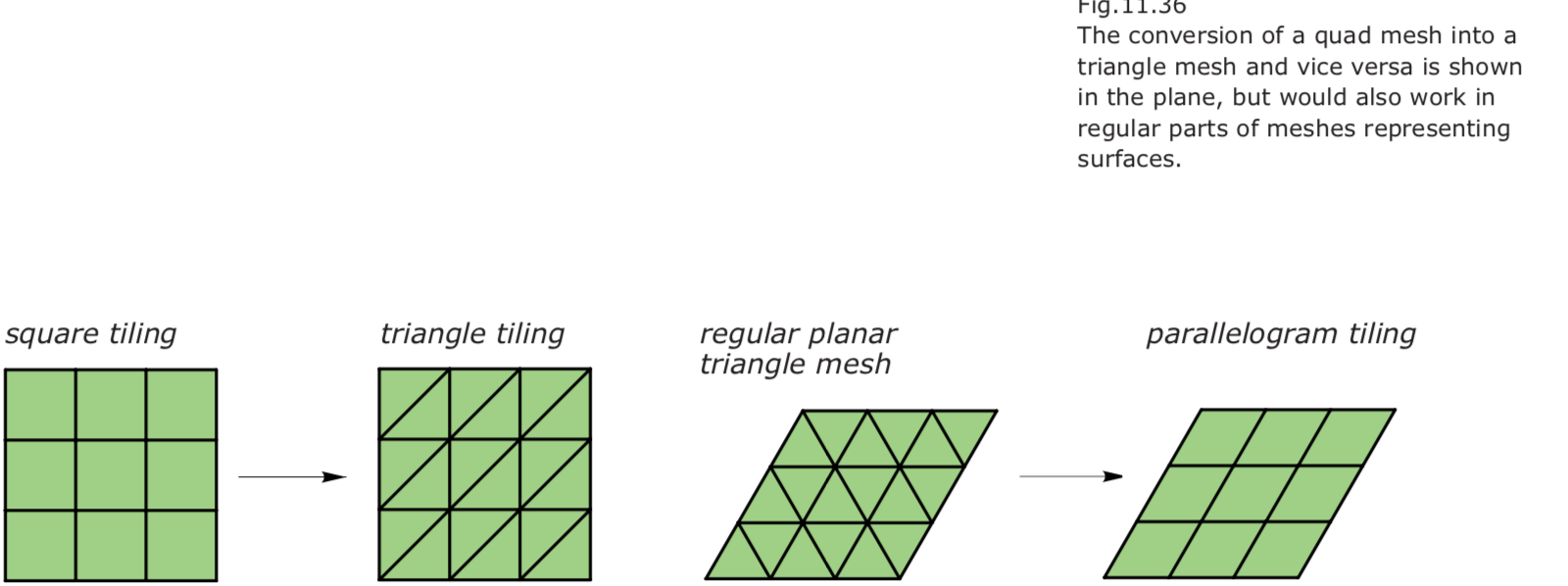
Quadrilateral meshes:
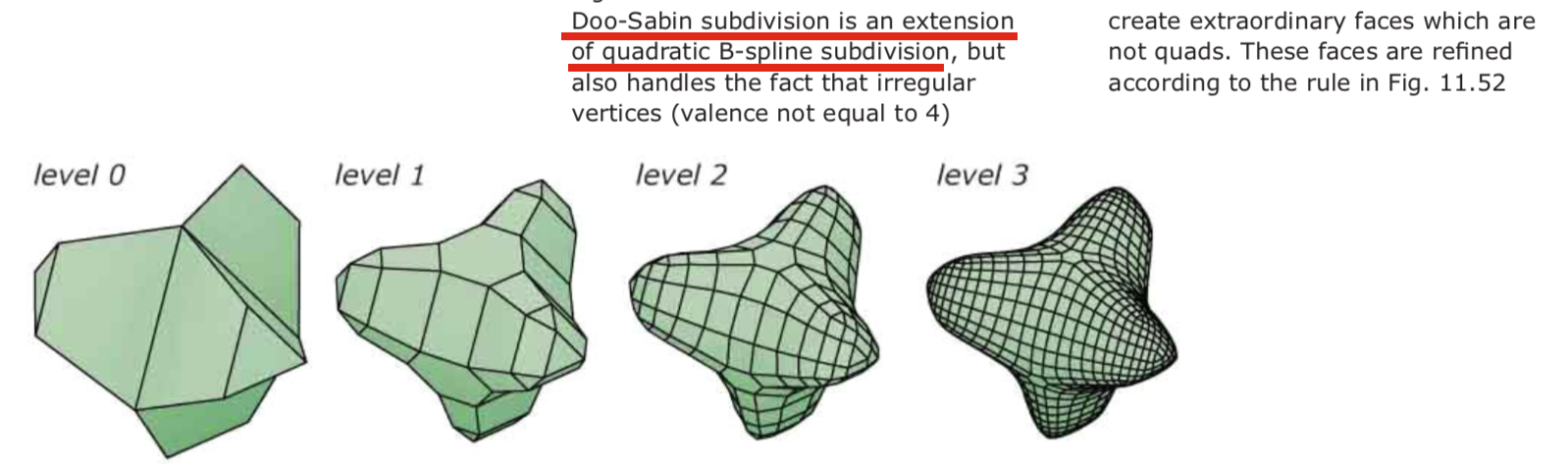
In a quad mesh, an interior vertex of valence 4 is called a regular vertex. If the valence is different from four, we talk about an irregular vertex.
Triangle meshes:
- Triangle meshes are well suited for architecture because their faces are planar.
- we may roughly need twice as many triangles as quads to represent the same shape
Hexagonal meshes:

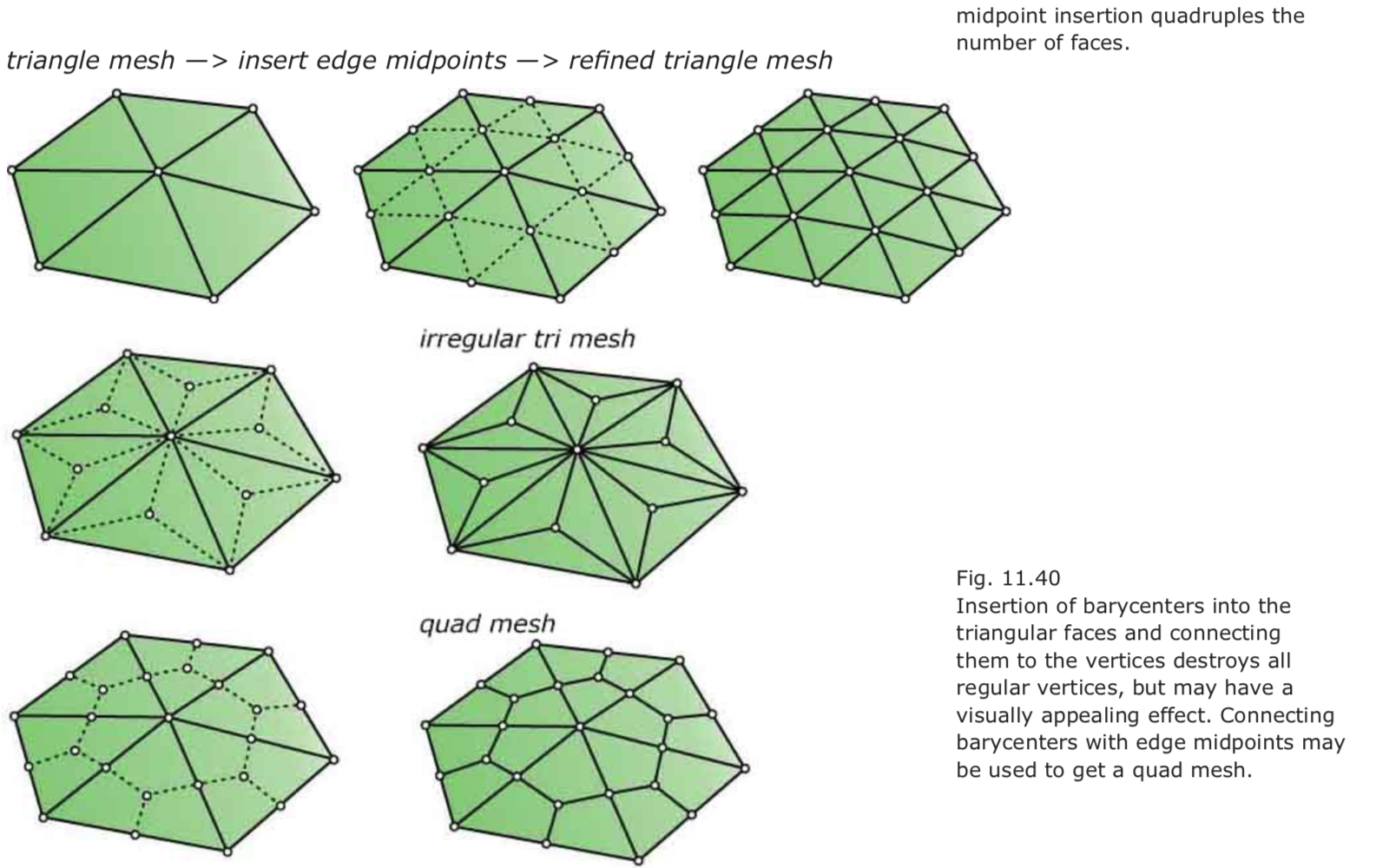
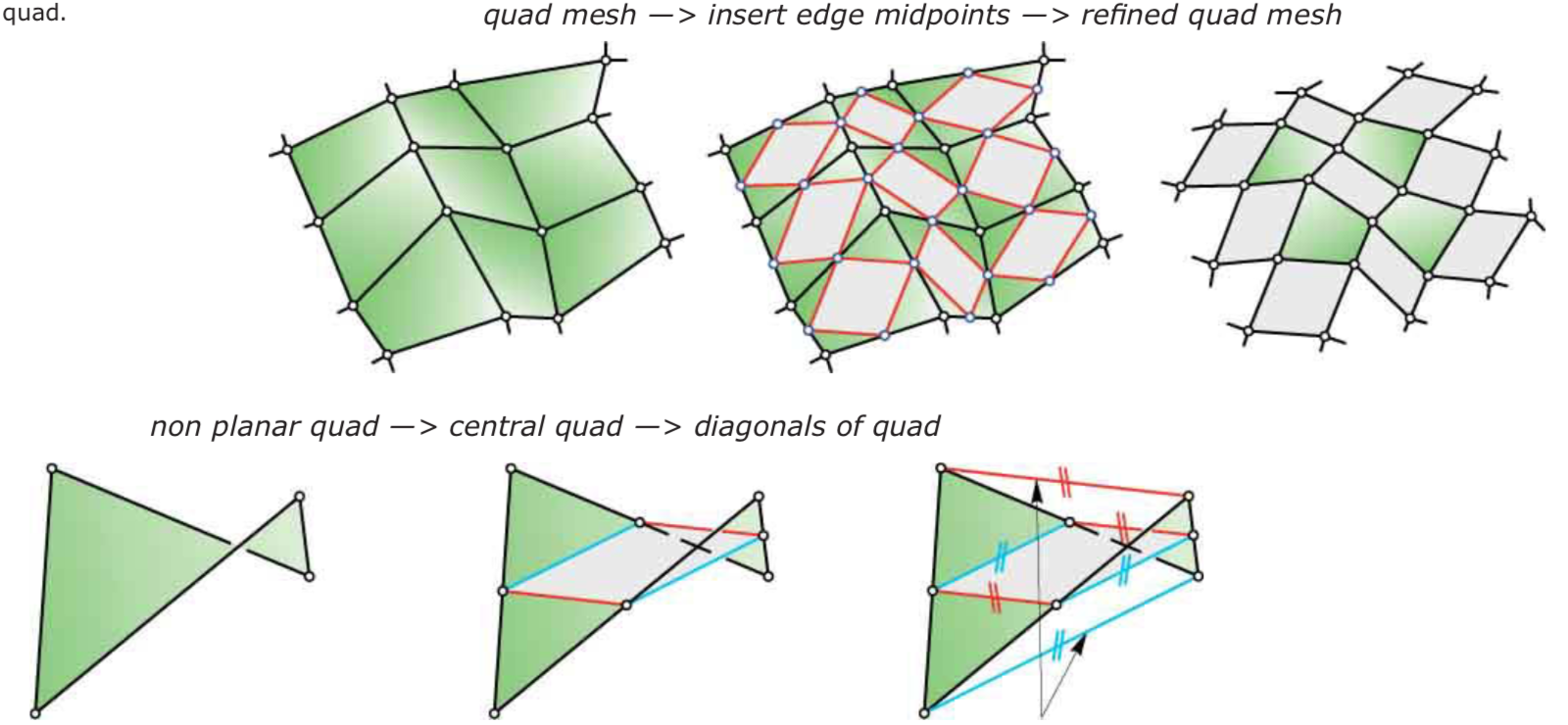
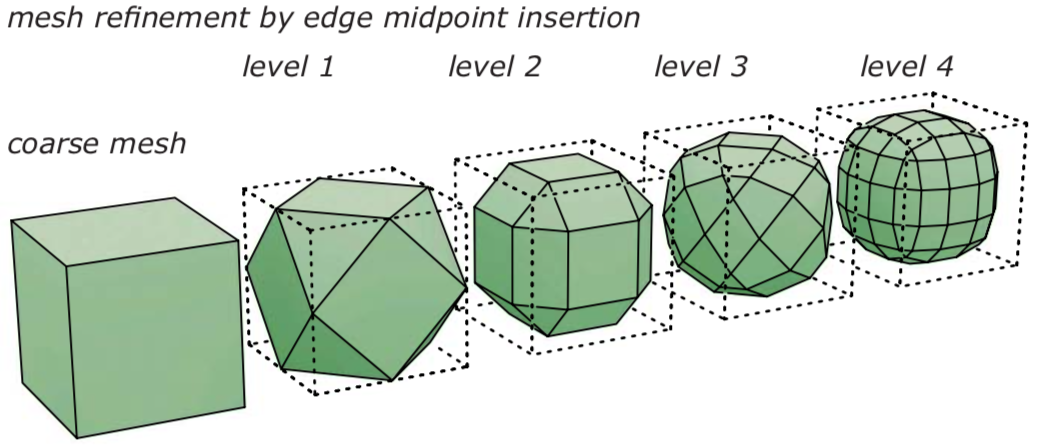
Mesh refinement:
It is useful to think about refinement as a two-step procedure:
- change the connectivity (number of vertices and the way they are connected)
- and then change the geometry (the position of the vertices).
Mesh decimation
reverse of mesh refinement (mesh decimation)
Aesthetics of meshes and relaxation:
- One basic idea is to adjust all mesh vertices so that the resulting mesh consists of nearly regular faces only.
- A related idea is a physical interpretation using a so-called mass-spring simulation system.
- one implements the vertices as mass points and the edges as springs.
- Then, one fixes some points (e.g., all boundary vertices) and lets the other vertices move freely until the entire system achieves an equilibrium . -This technique is called relaxation.

Subdivision Surfaces

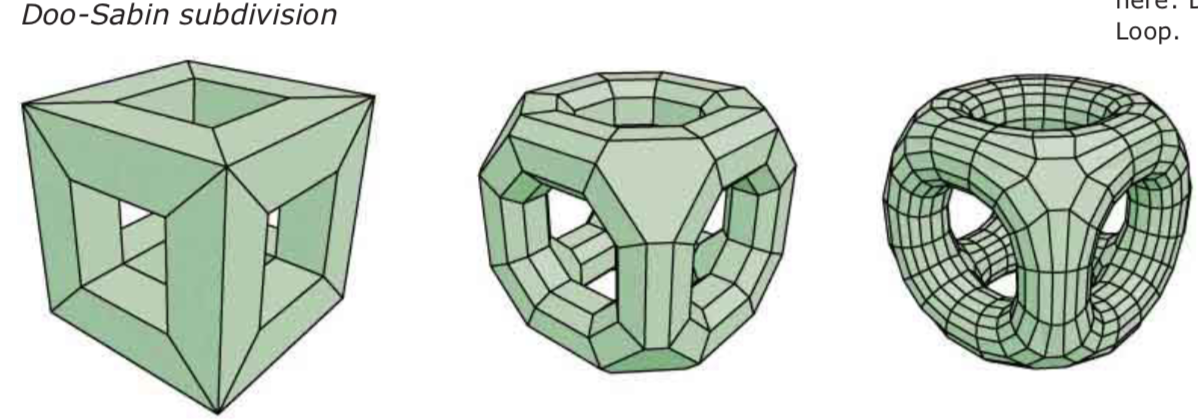
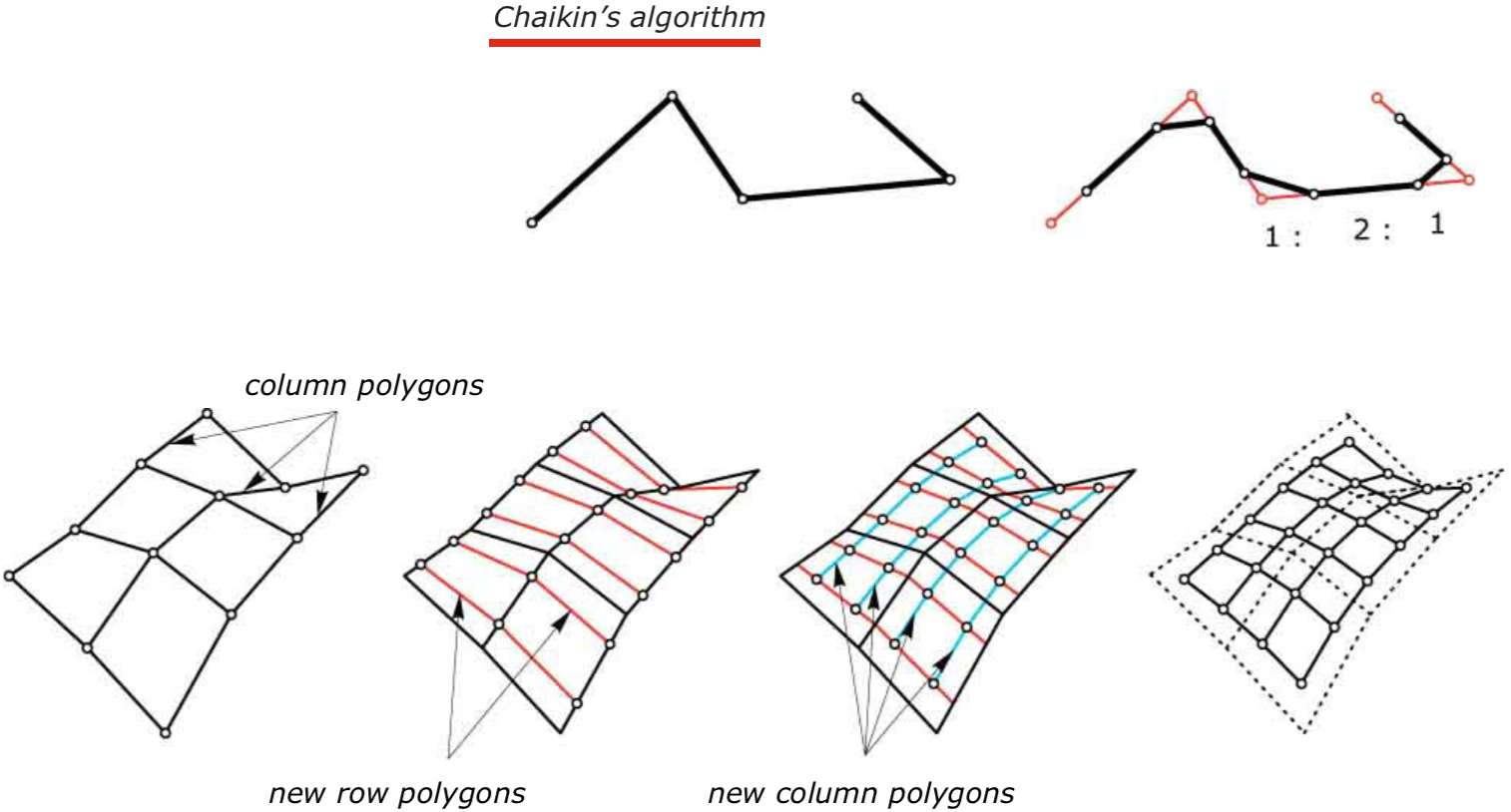
Quadratic B-spline surfaces via subdivision:
Doo-Sabin subdivision scheme:
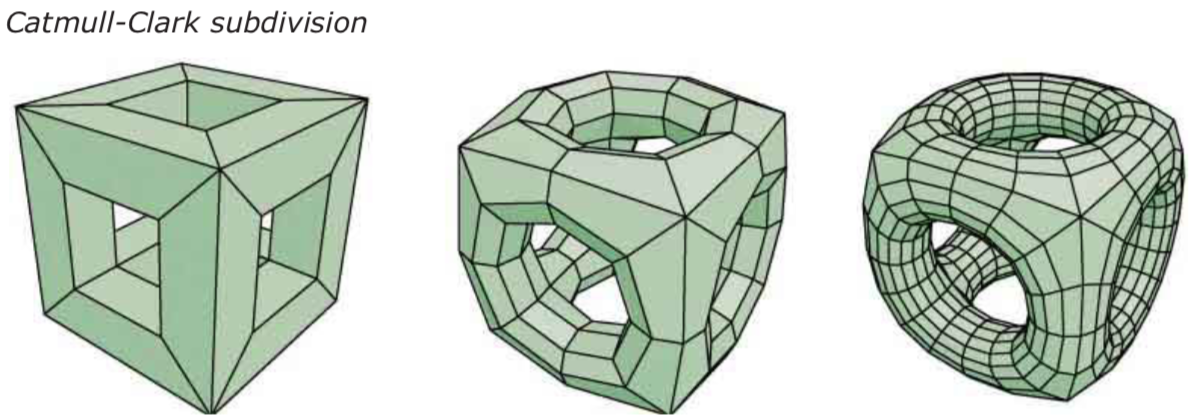
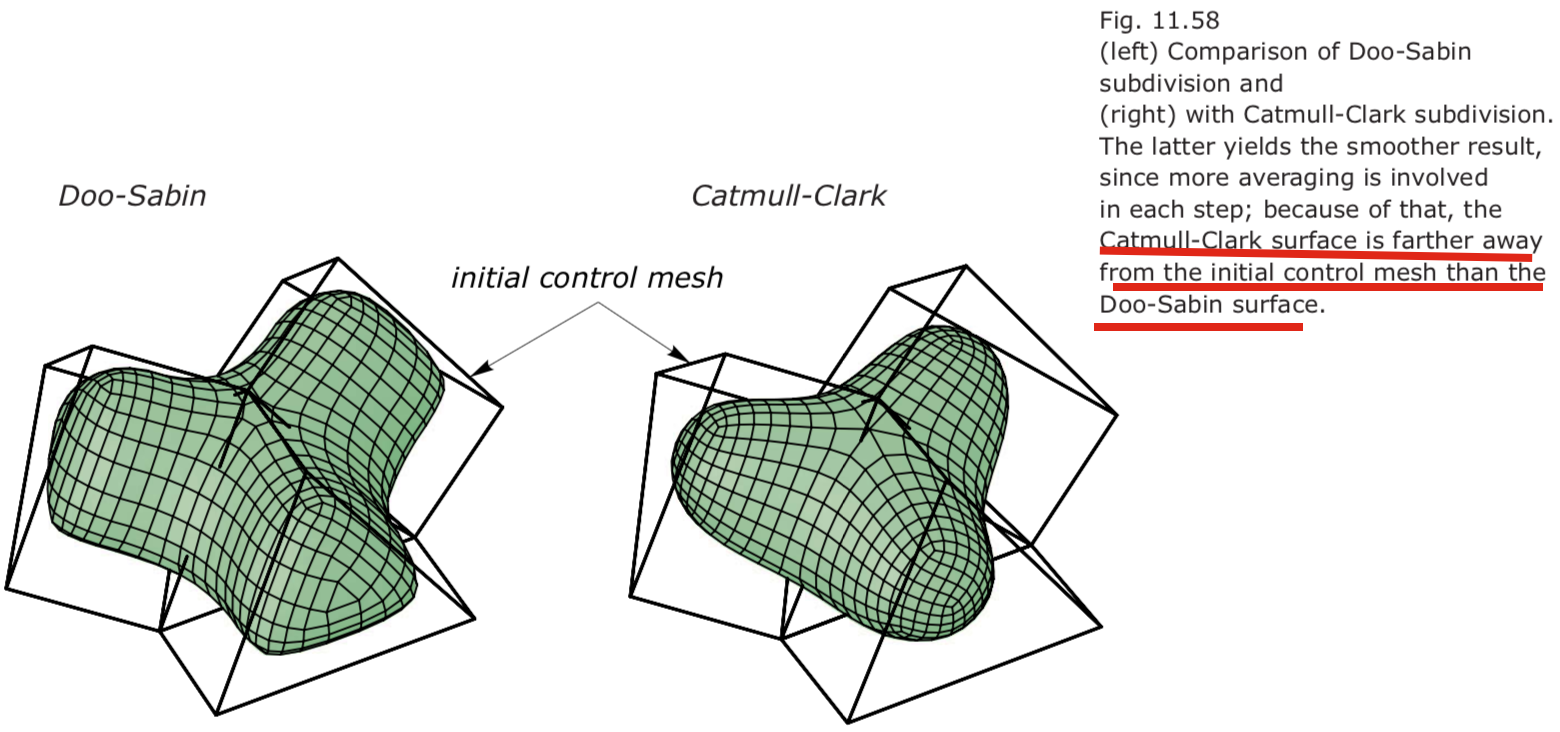
From cubic B-splines to Catmull-Clark subdivision:
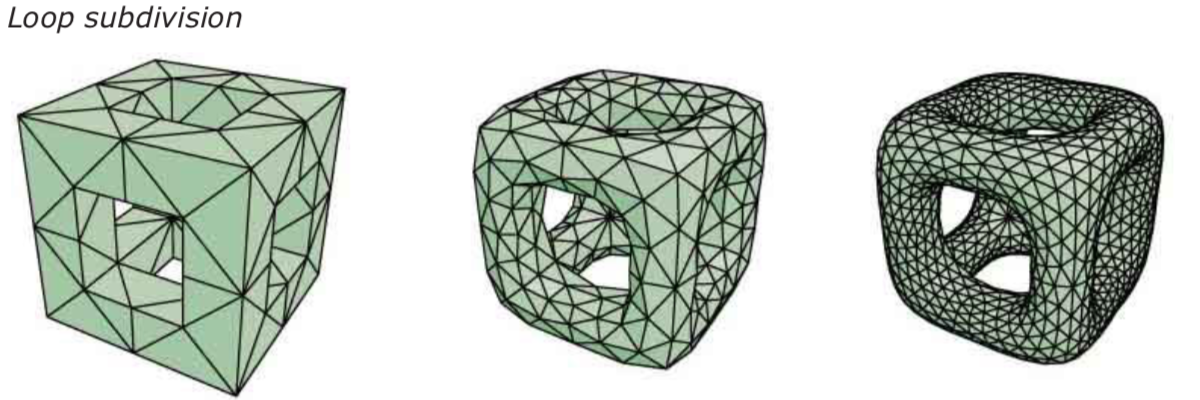
Triangle-based subdivision:

