Motions, sweeping, and shape evolution

kinematic geometry = geometry of motions

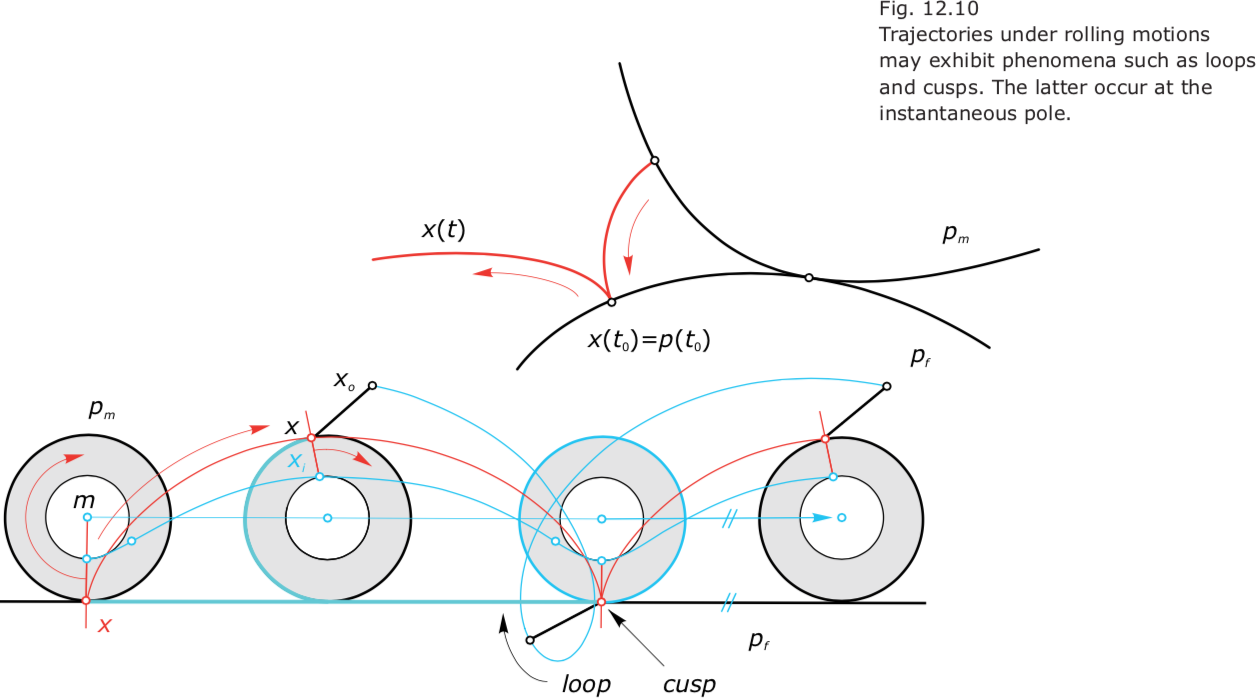
Motions in the plane

However, there is some systematic behavior, and the simplest is the following: At any time instant t0, the normals to the trajectories pass through a point p(t0) (or they are parallel).

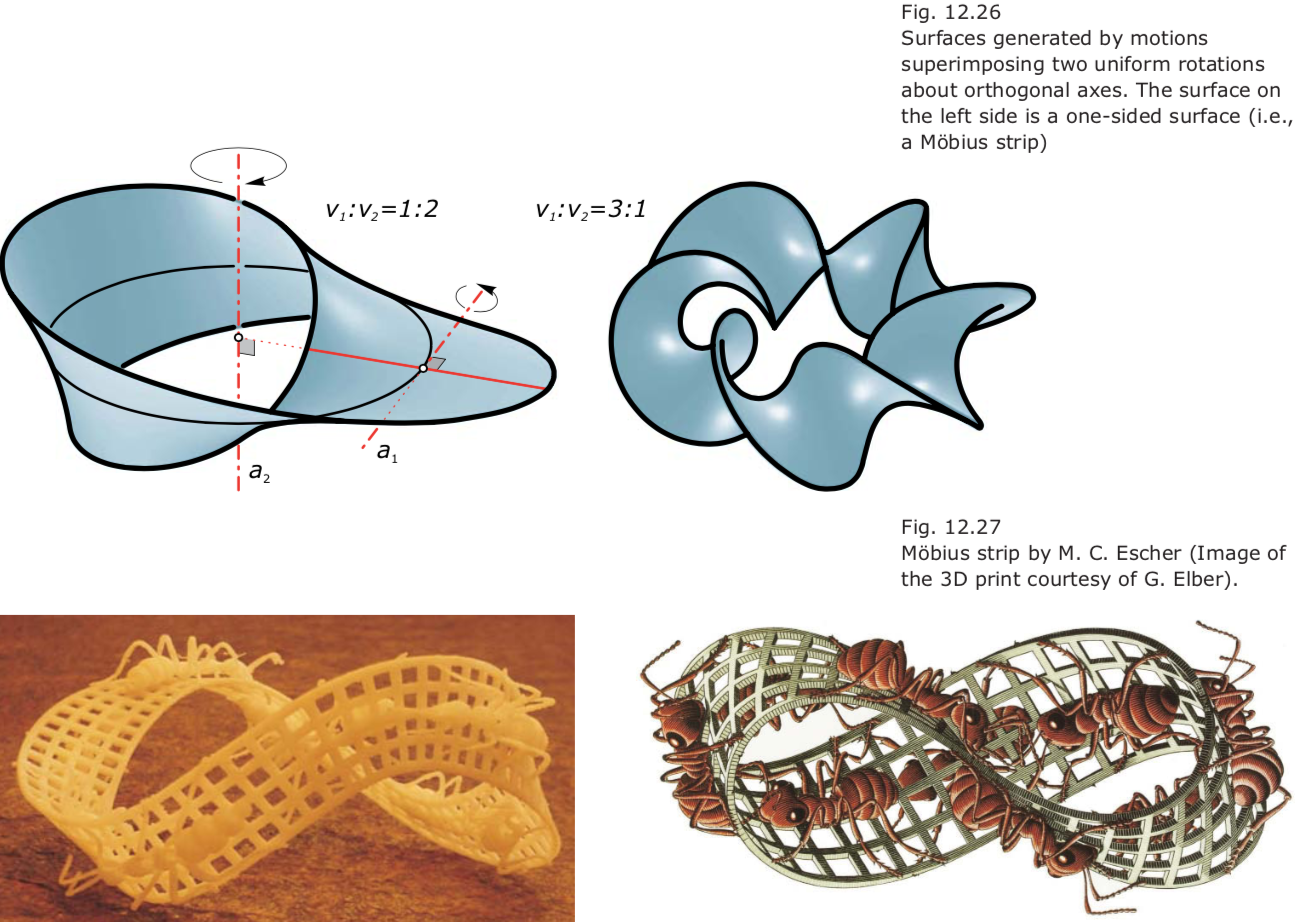
Spatial Motions

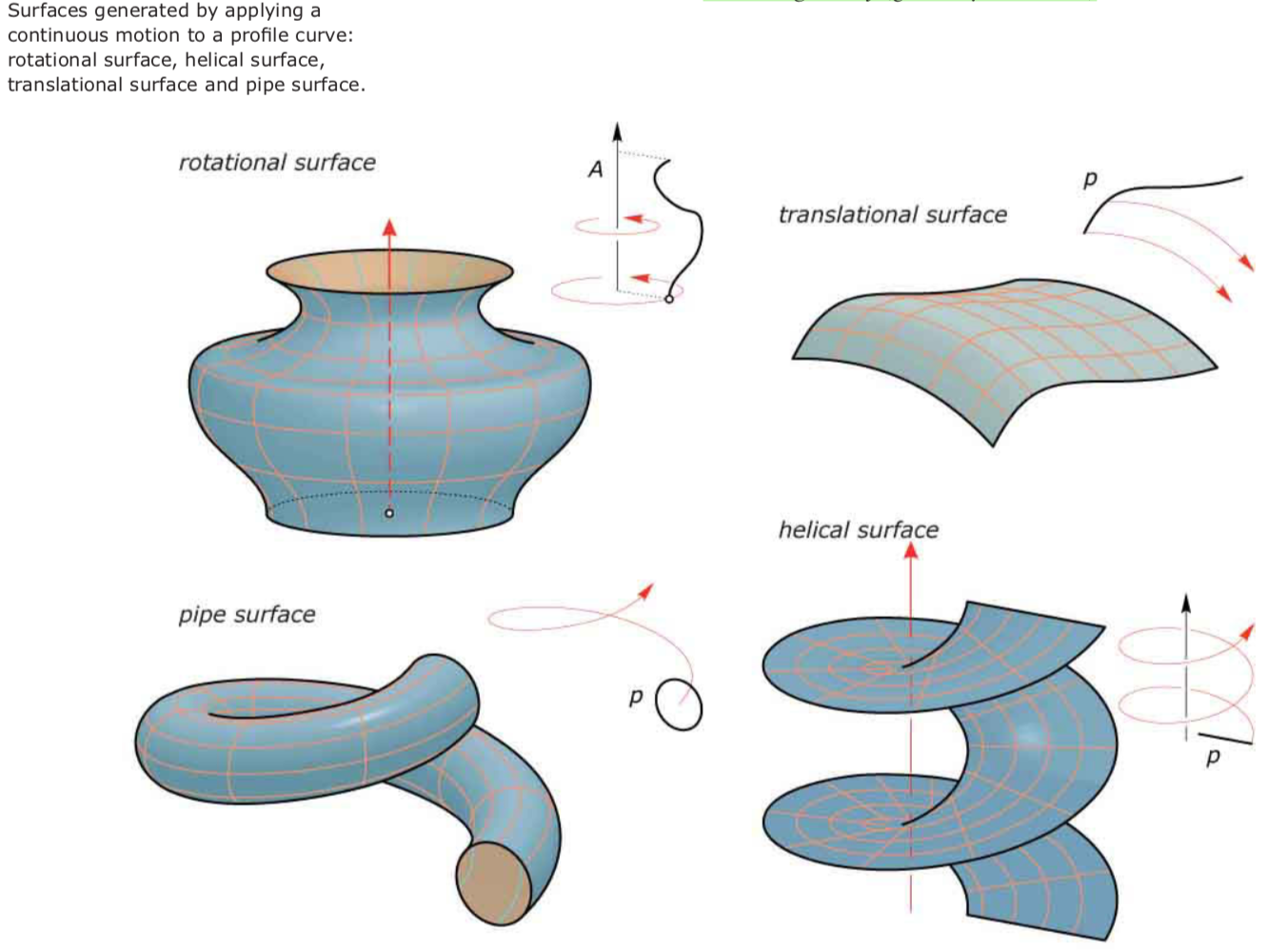
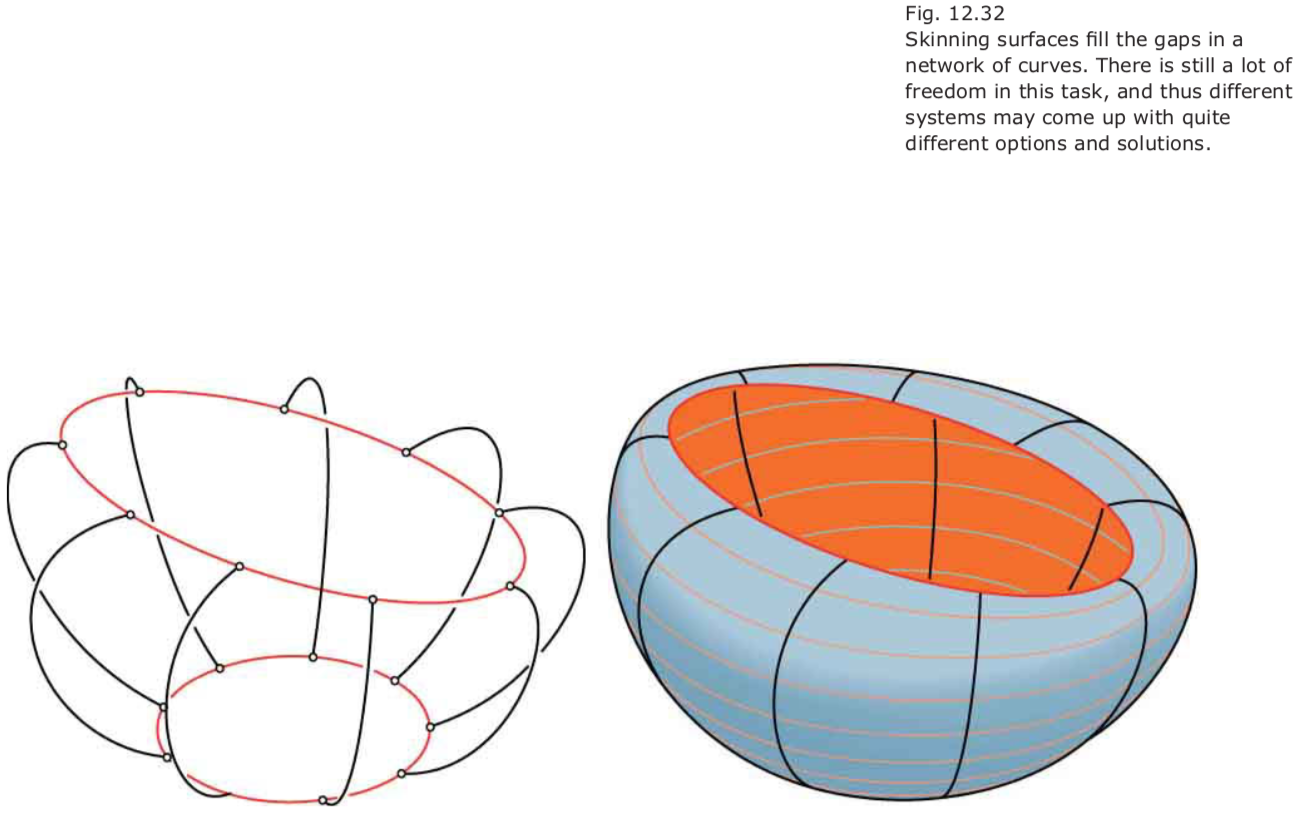
Sweeping and Skinning

Whereas sweeping often does not allow us to precisely prescribe the location of the sources in space, there is a method for doing so. It is called skinning, which wraps a surface (skin) over a given network of curves.

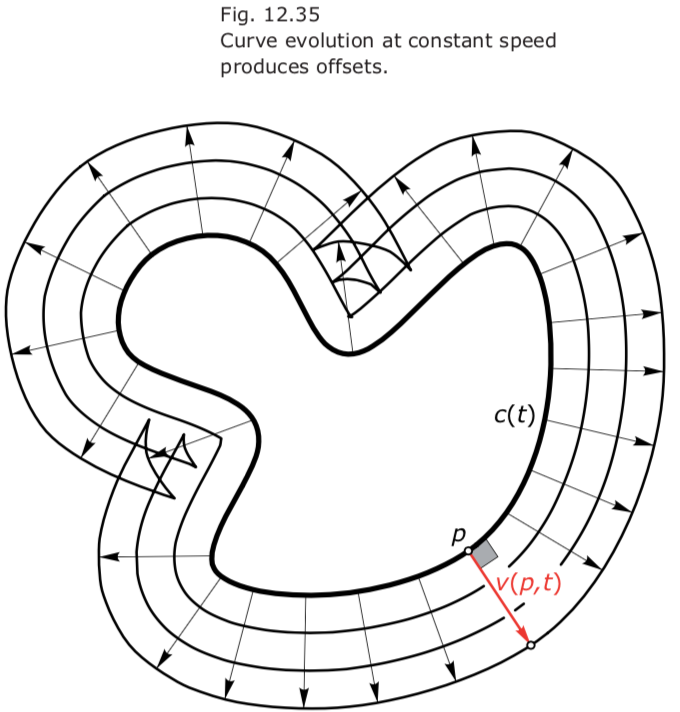
Curve Evolution

evolutions of curves = curve flows

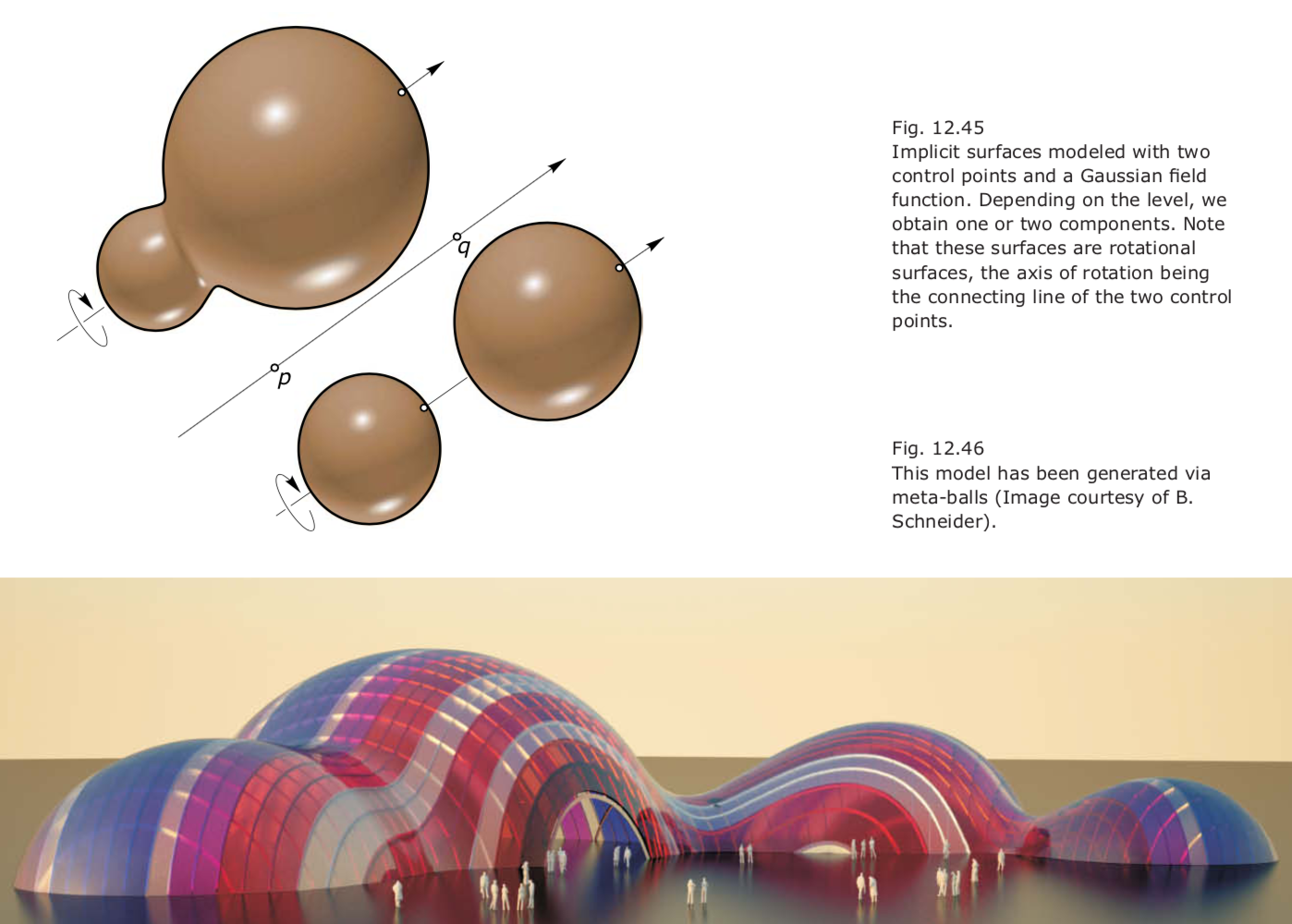
Metaballs and Modeling with Implicit Surfaces

• One calls the set of points on c the zero level set of f because for all points of c the value of f is 0.
• The representation of a curve as a level set of a function is also known as implicit representation.
• We may look at other level sets of f (also denoted as isolines or isocurves of f), which are the loci of points where f has the same value k. $f(x,y) = k$
• If we define the new function $g(x,y) = f(x,y) – k$ the k-level set of f appears as the zero-level set of g.
• Any implicitly represented curve c: f(x,y) = 0 may be embedded into a family of level sets f(x,y) = k. By variation of k, we obtain a mathematical description of a curve evolution.