Deformation 变形

Three-Dimensional Transformations 3D变换

• Affine maps 仿射映射：
  
  1. 直线映射成直线
  2. 平面映射成平面
  3. 保直线和平面的平行性
  4. 不改变共线点比例
• Projective maps 射影映射：
  
  1. 直线映射成直线
  2. 平面映射成平面
  3. linear functions [f = (f0 + f1x + f2y + f3z)/D] with a common denominator D = d0 + d1x + d2y + d3z. if d1 = d2 = d3 = 0 (d0 ≠ 0) we have an affine map. Otherwise, d0 + d1x + d2y + d3z = 0 determines a plane V whose points are mapped to points at infinity.
• Nonlinear transformations
  not all straight lines are mapped to straight lines

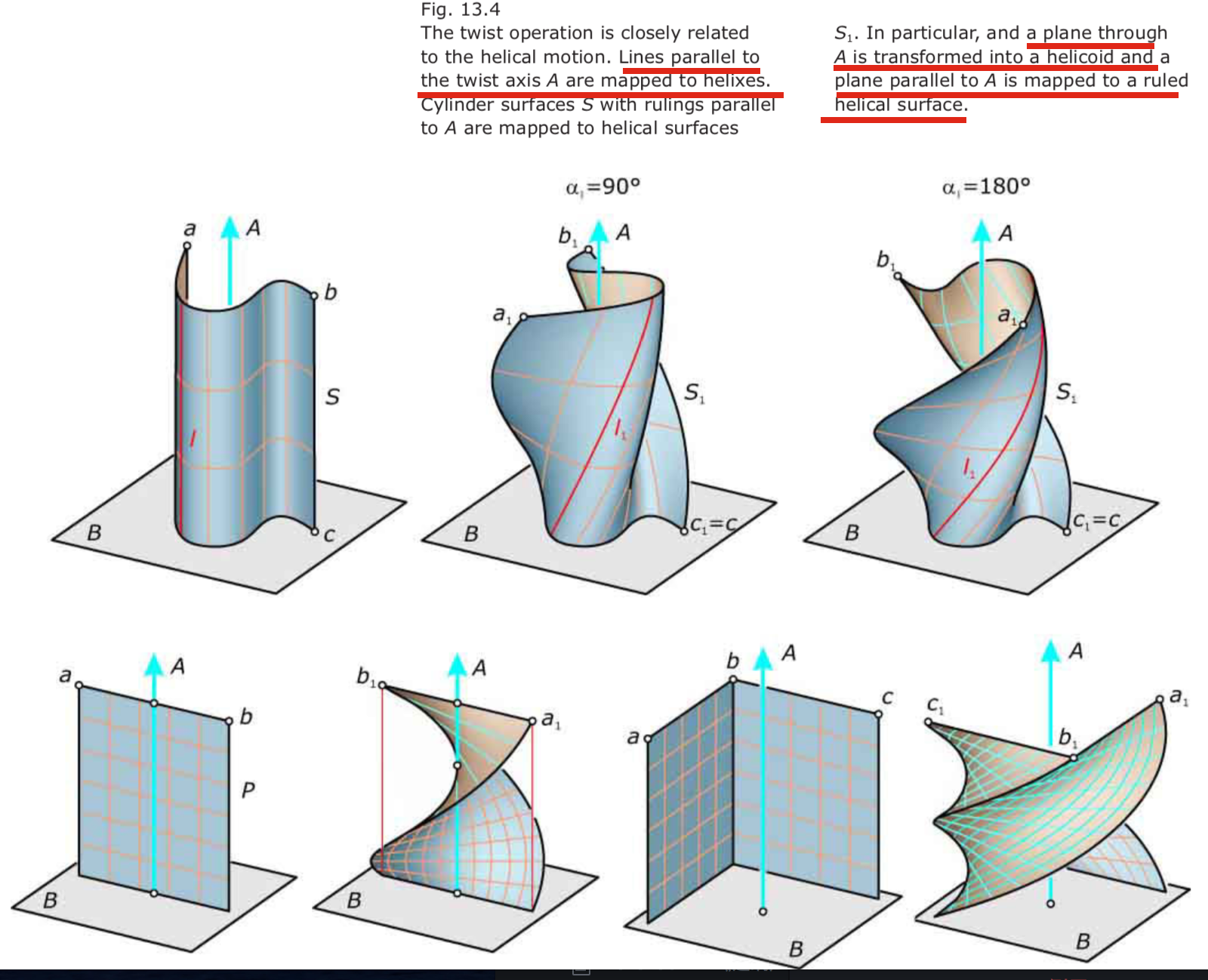
Twisting 扭曲

The bottom plane B remains fixed and the rotational angle αmax of the top plane T is prescribed. We assume that the distance between the bottom and top planes is h, the height of the object to be deformed. The rotational angle α(z) of the slice at height z above B is selected to be α(z) = (z/h) α_{max}.

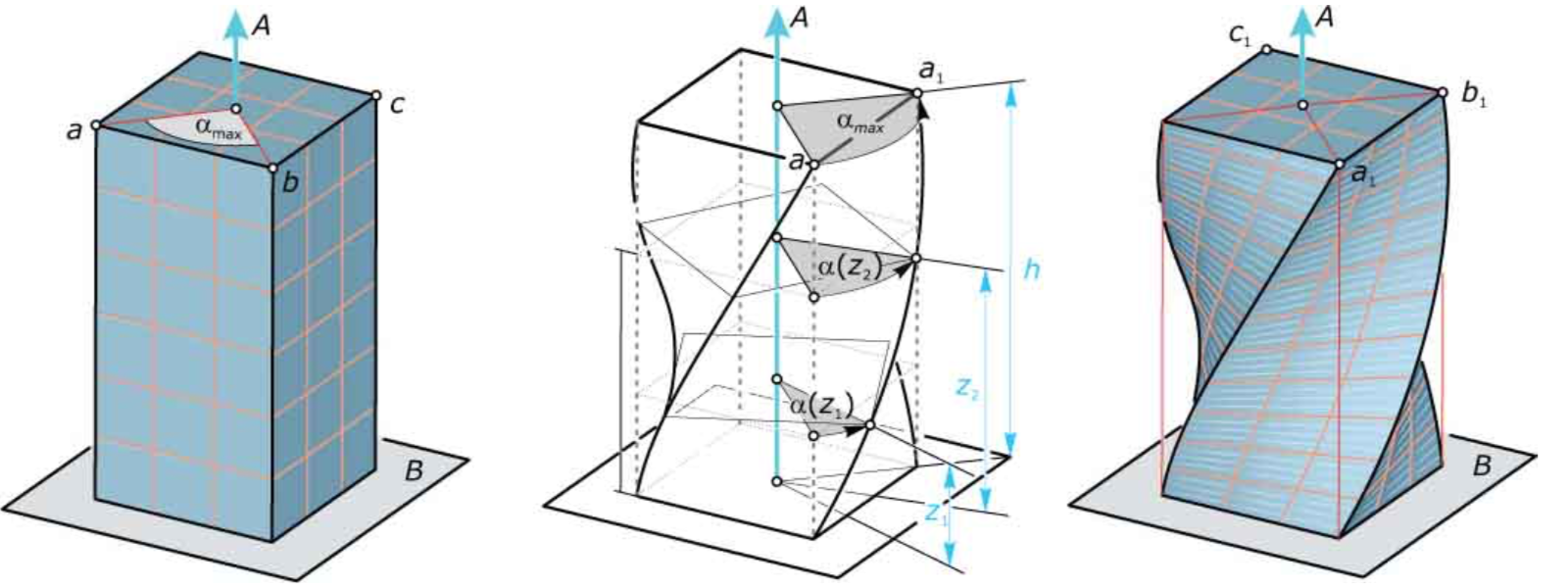
• interesting property of the twist operation is that it preserves the volume.

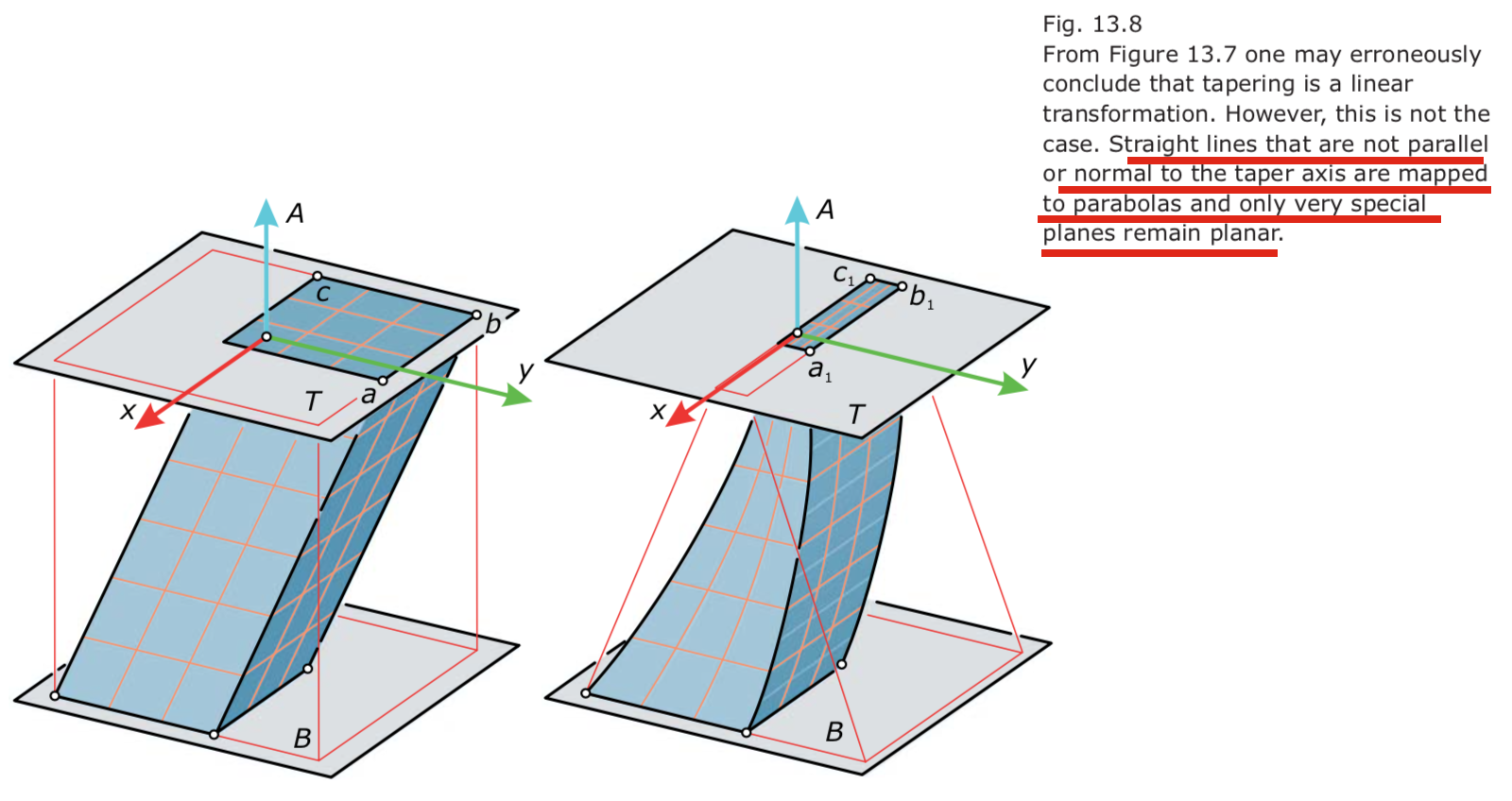
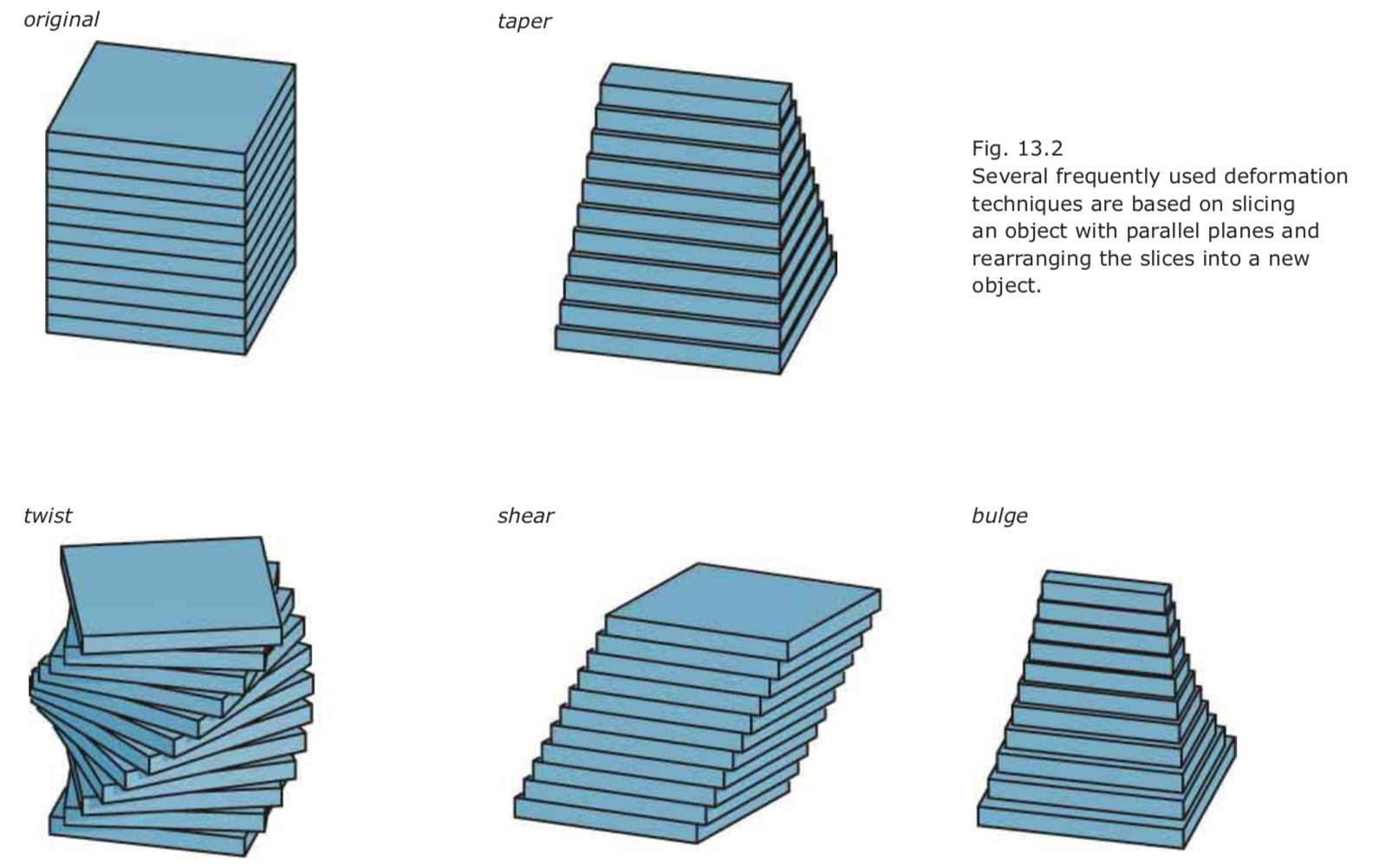
Tapering (~scaling)

• We select a reference plane B (say, the bottom plane) and an orthogonal axis A.
• All points of B and all points of A remain fixed under tapering.
• One then changes the object by scaling the slices in planes orthogonal to A (i.e., parallel to B).
• Tapering is not a linear transformation. It is a special quadratic transformation.
• Bulge. If one wants to have thickening or thinning effects without loss of smoothness, one can use a deformation technique sometimes called bulge.

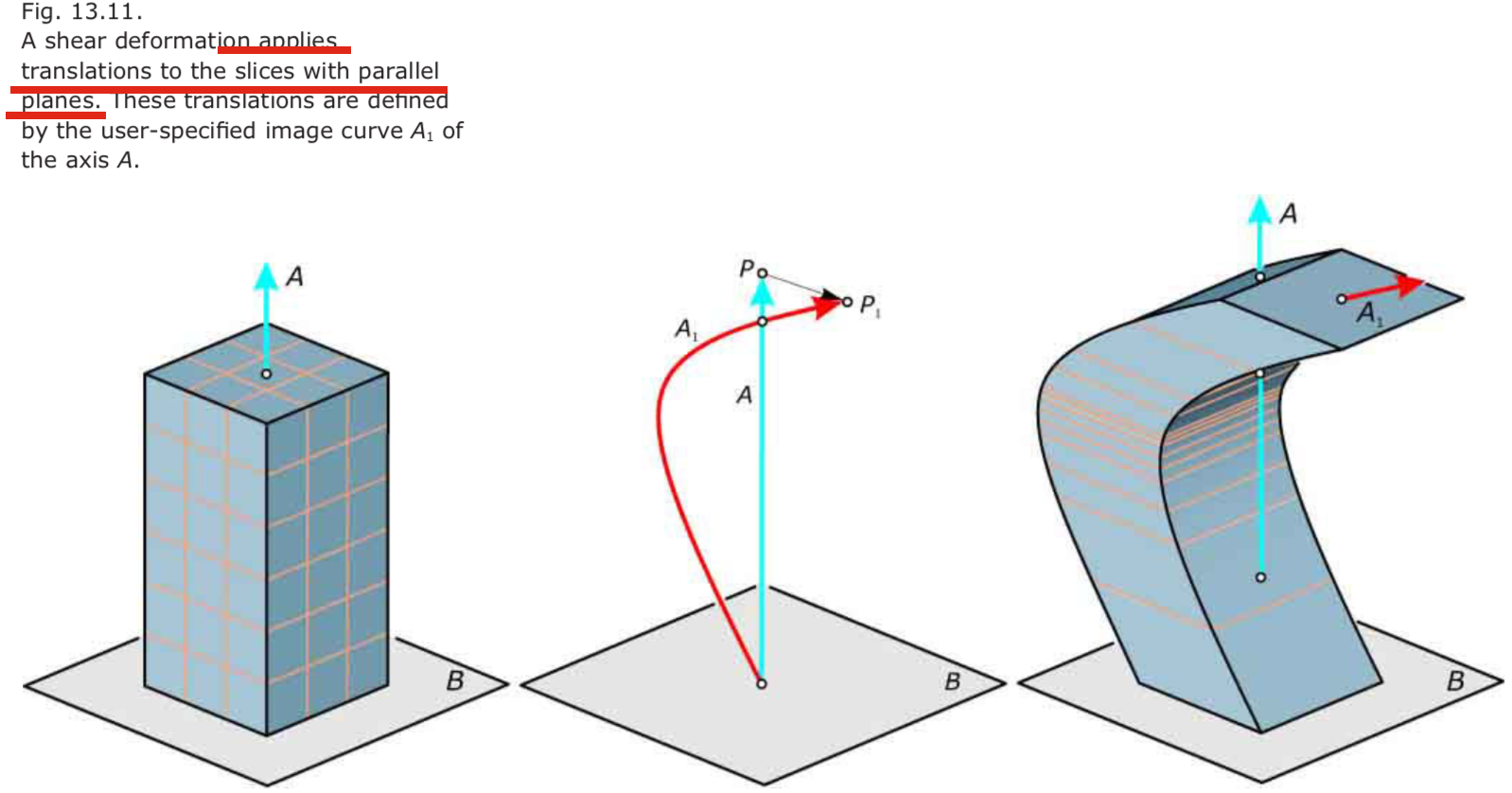
Shear Deformations

• Shear deformations apply translations to the slices
• shear transformations are therefore volume preserving.

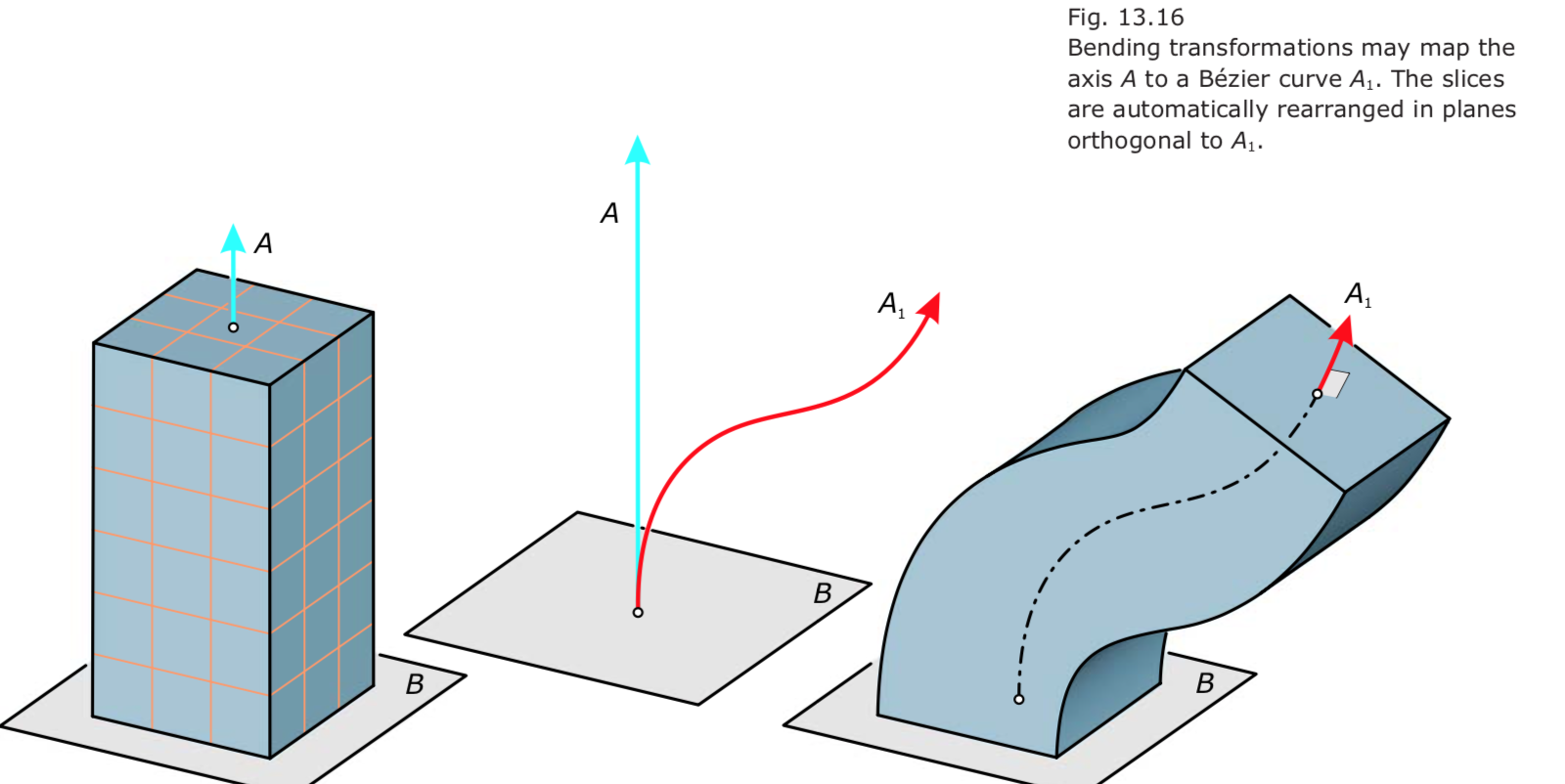
Bending 弯曲

• bending deformations that also change the orientation of the slices.

Freeform Deformations 自由形变换

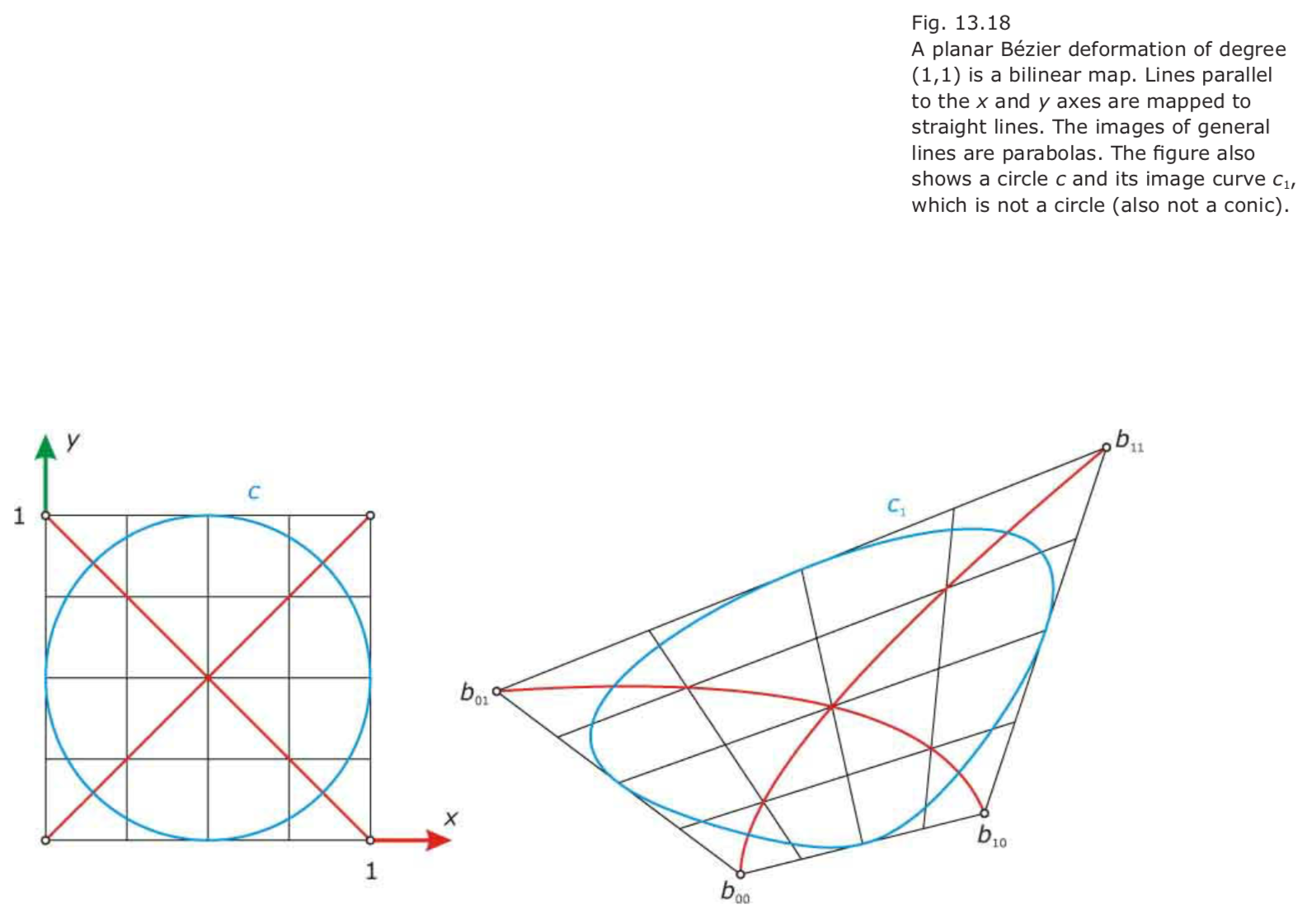
• Planar Bézier deformations of degree (1,1).

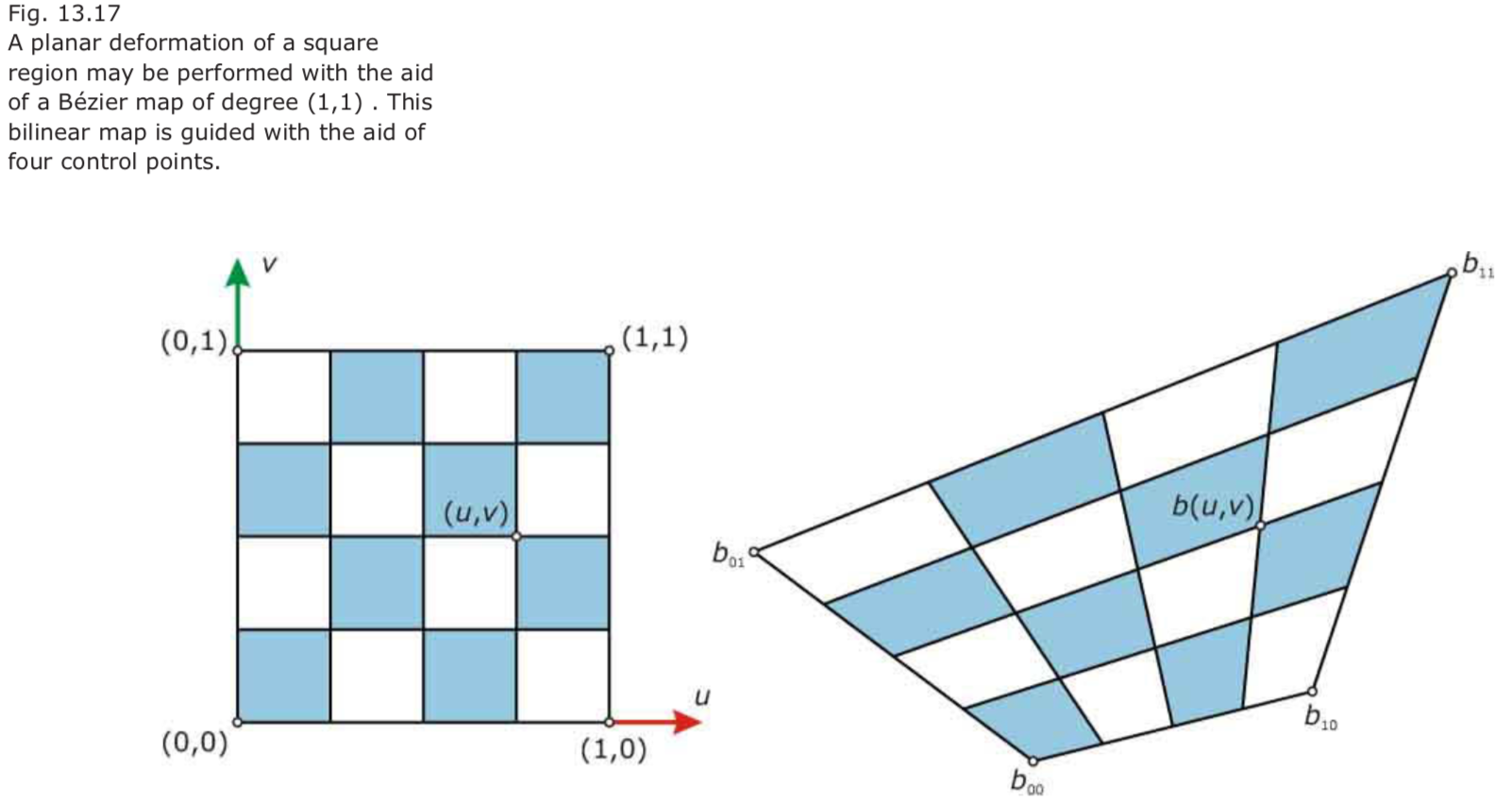
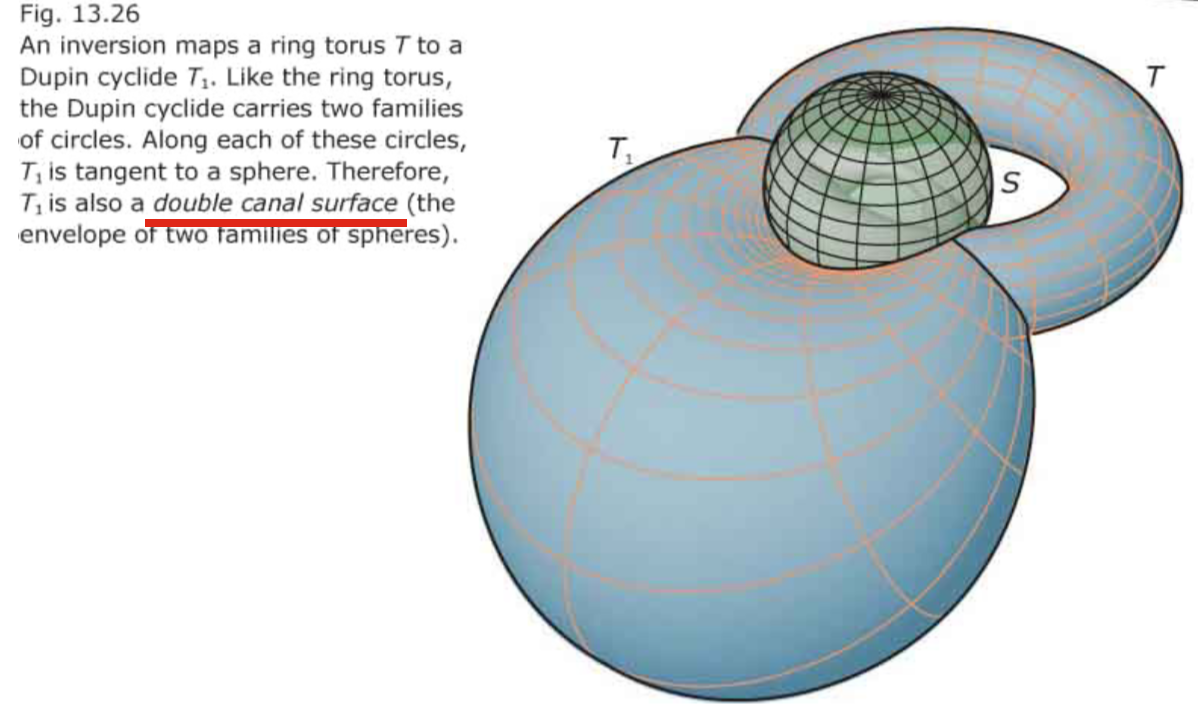
Inversions 倒置

• The inversion with respect to a sphere maps
  (a) straight lines to circles through the center o and
  (b) planes P to spheres P1 through o.
  (c) Spheres (which do not pass through o) are mapped to spheres and circles (not through o) are mapped to circles.

Three-Dimensional Textures 3D纹理

• One views a three-dimensional texture as a topographic surface [i.e., the graph surface of a height field, which associates to each point p1 of a surface S1 a height h(p1) of the texture].