Visualization and analysis of shapes

• certain undesirable effects (such as small bumps) may only be seen from a particular perspective under special lighting conditions.
• Here, curvature of surfaces comes into play.
• In fact, the judgment of a shape as visually pleasing depends largely on the way in which curvature varies along the surface.

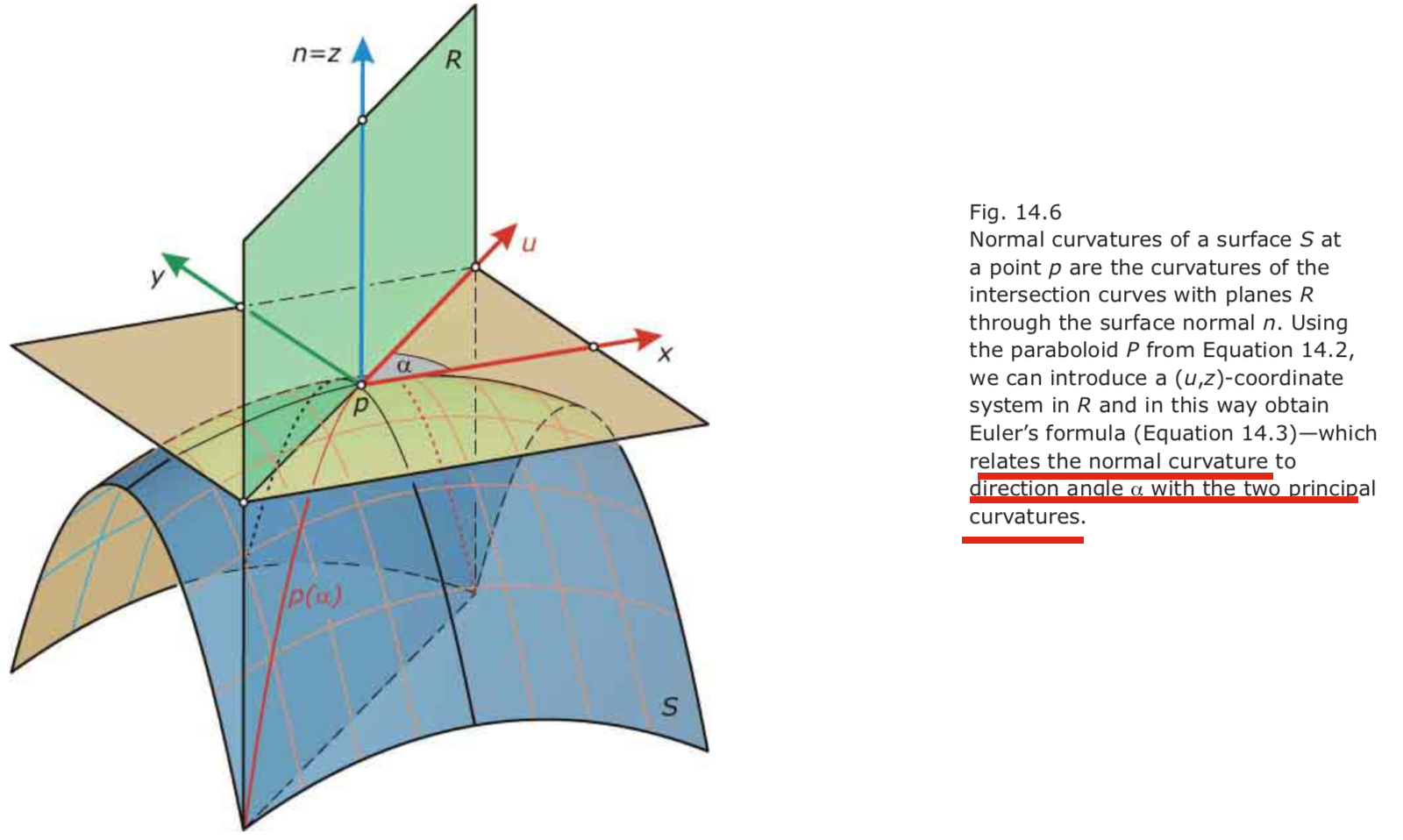
Curvature of surfaces 曲面的曲率

osculating parabola

\(g (x) = f (a) + f '(a)(x – a) + 1⁄2 f ''(a)(x – a)^2.\)

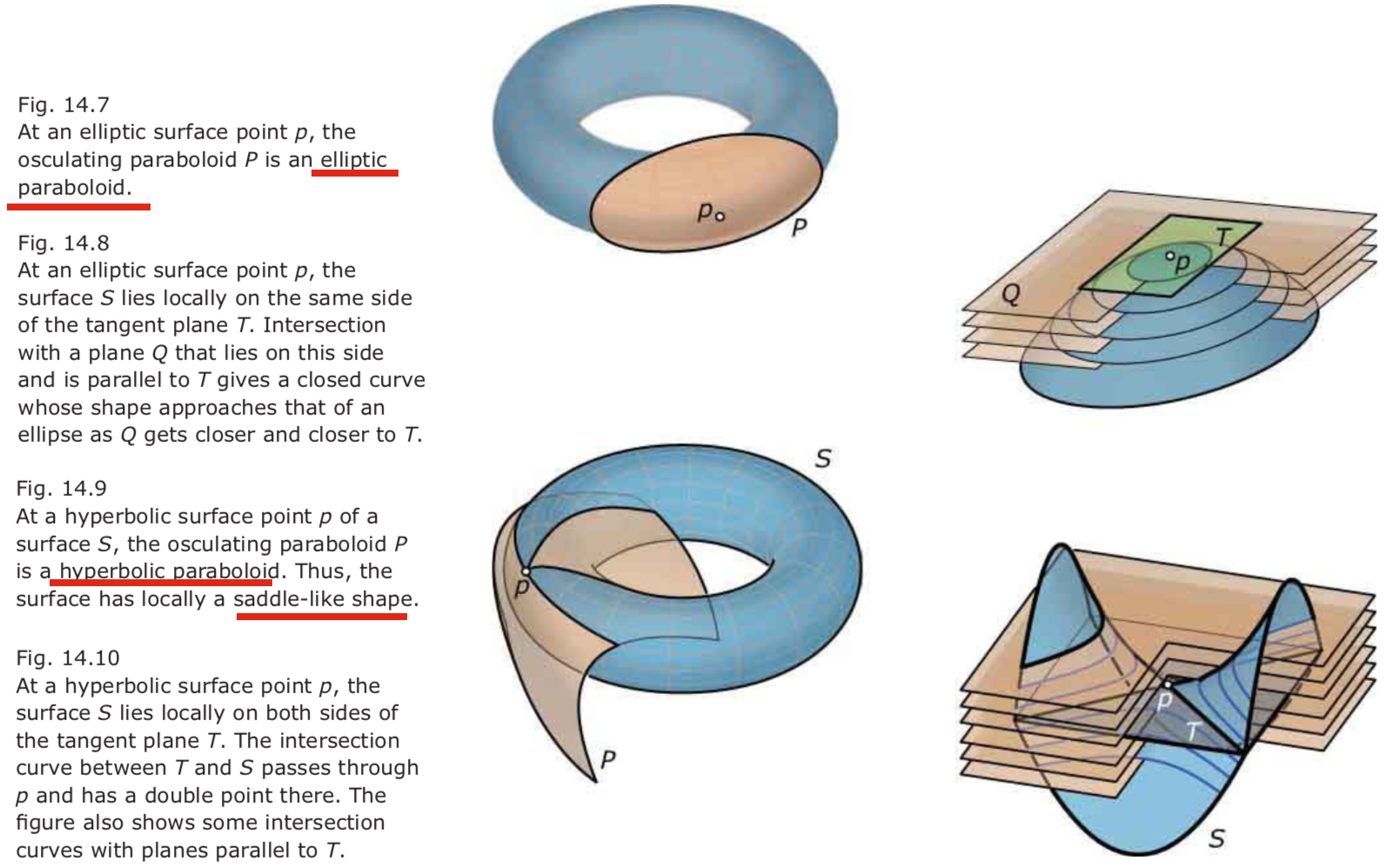
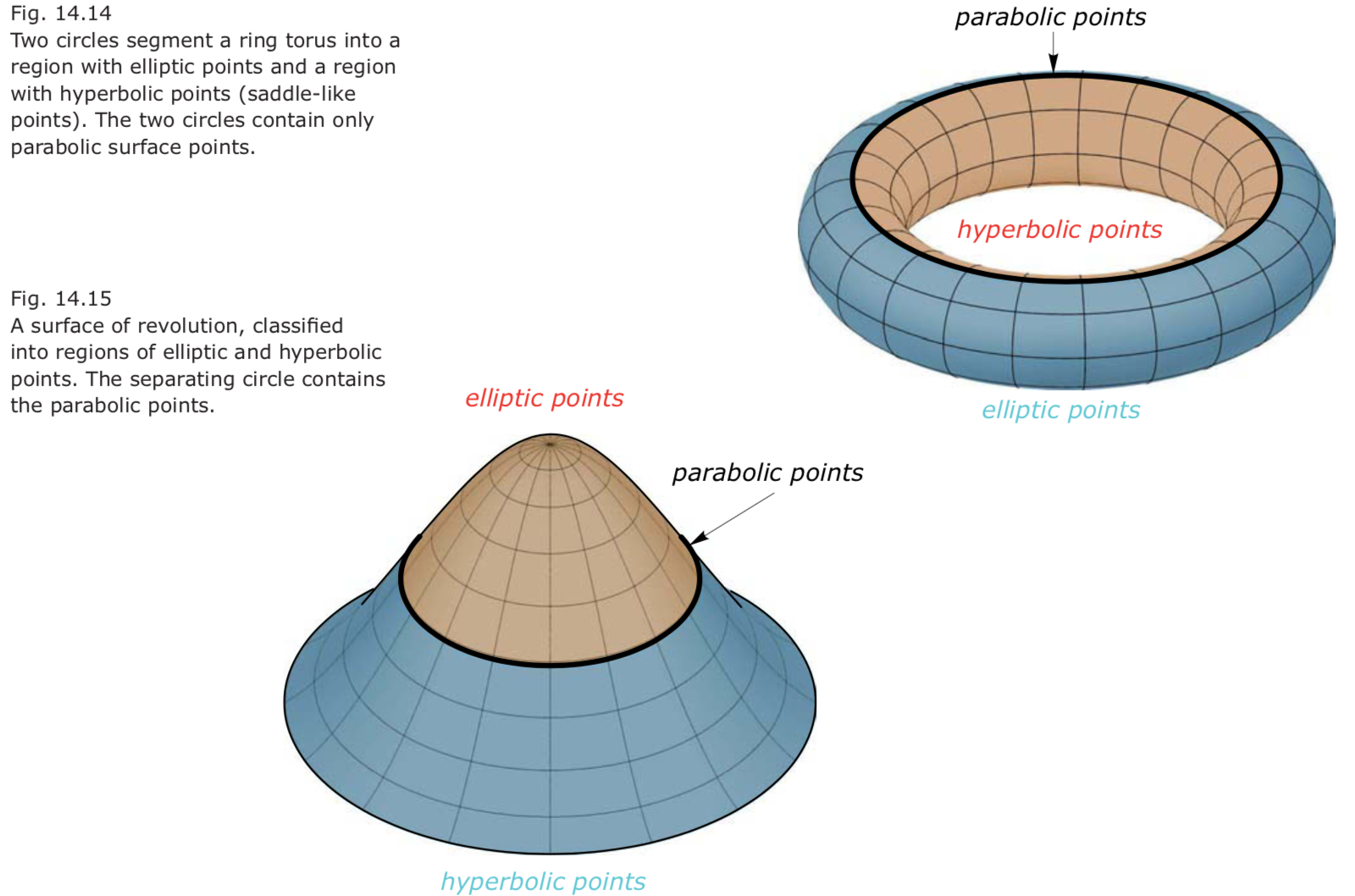
Classification of surface points.

1. Elliptic surface point
2. Hyperbolic surface point.
3. Parabolic surface point.
4. Flat point.

freeform surface

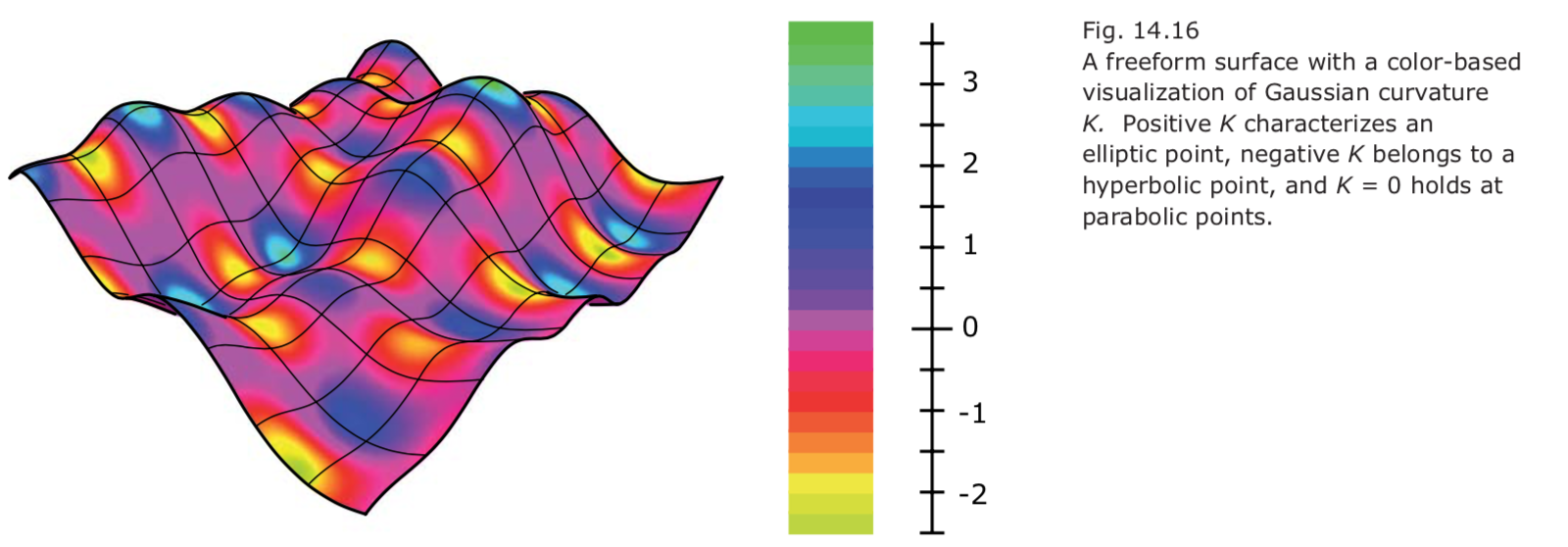
Gaussian Curvature

• Gaussian curvature measures the local area distortion under the Gaussian spherical mapping.
• Gaussian curvature is preserved under isometric mappings.
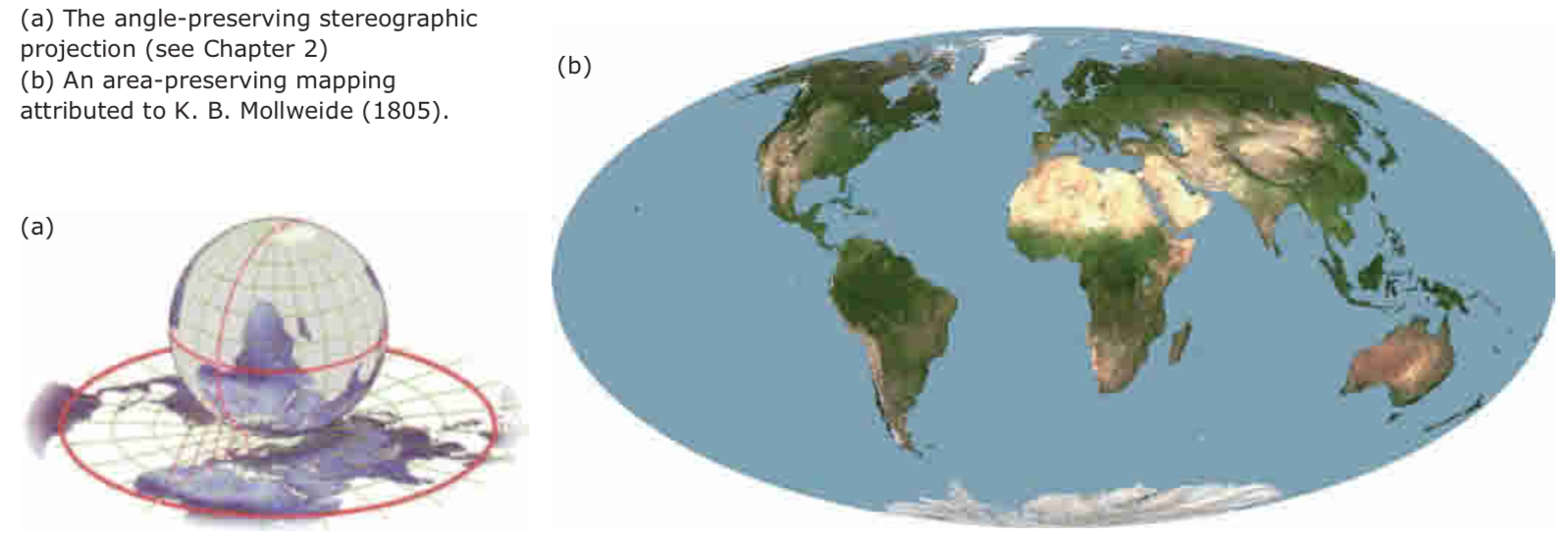
• there is no distortion-free map of the earth.
• an isometric mapping S → S1 also preserves the intersection angles between curves. Moreover, it preserves surface areas: a domain B in S and its corresponding domain B1 in S1 have the same surface area.
• an angle-preserving mapping (also called conformal mapping) need not be an isometric one.
• In fact, there are many angle-preserving maps between any pair of surfaces. e, there are many area-preserving mappings.
• Frequently used mappings of the earth are either angle preserving or area preserving. However, they cannot have both properties because preservation of both angles and areas implies an isometric mapping.

Mean Curvature

• Mean curvature H = (k1 + k2)/2, the arithmetic mean of the principal curvatures. Surfaces with vanishing mean curvature are minimal surfaces, which appear (for example) as shapes of soap films through a closed wire.

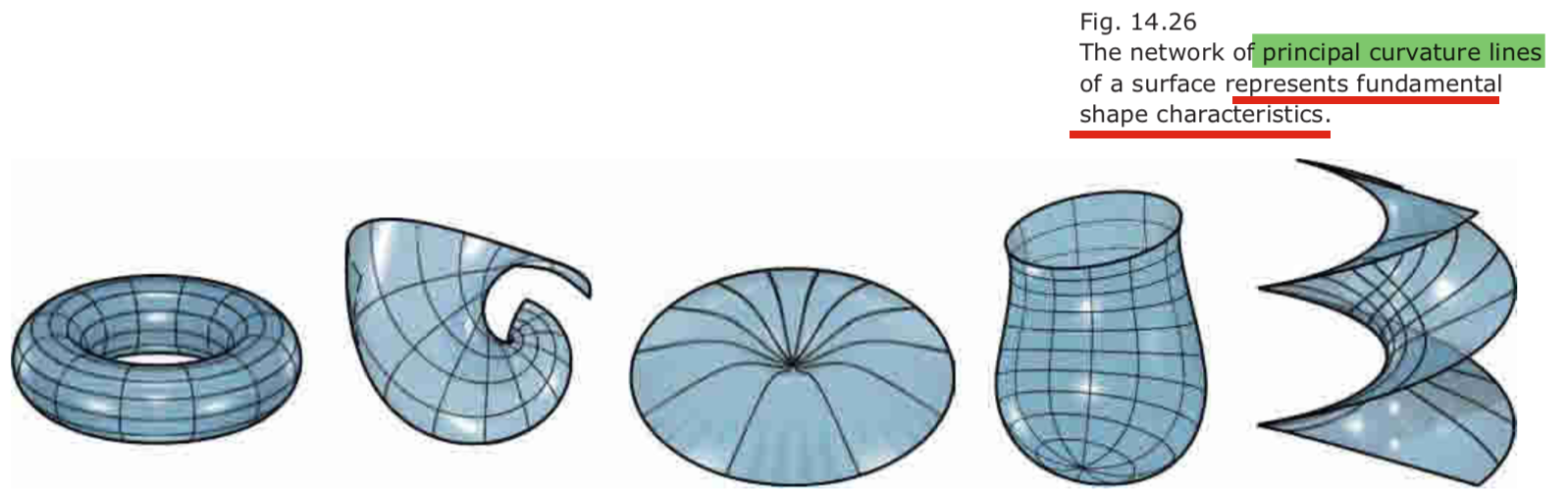
principal curvature lines

• A principal curvature line is a curve on a surface whose tangents are in principal direction.
• through each general point of a surface there are two principal curvature lines that intersect at a right angle and touch the principal directions.
• Principal curvature lines or related networks of curves are sometimes used for the generation of surface illustrations that aim at results that are similar to drawings made by artists.

umbilics

• The principal directions are uniquely defined only if k1 and k2 are different. For k1 = k2, we have a special surface point called an umbilic.
• the osculating paraboloid P is a paraboloid of revolution or a plane (k1 = k2 = 0).
• A sphere S (radius R) has only umbilics.
• At an umbilic, we have the same curvature behavior as for a sphere or a plane; in the latter case we also speak of a flat point.
• At an umbilic the network of principal curvature lines has a singularity.

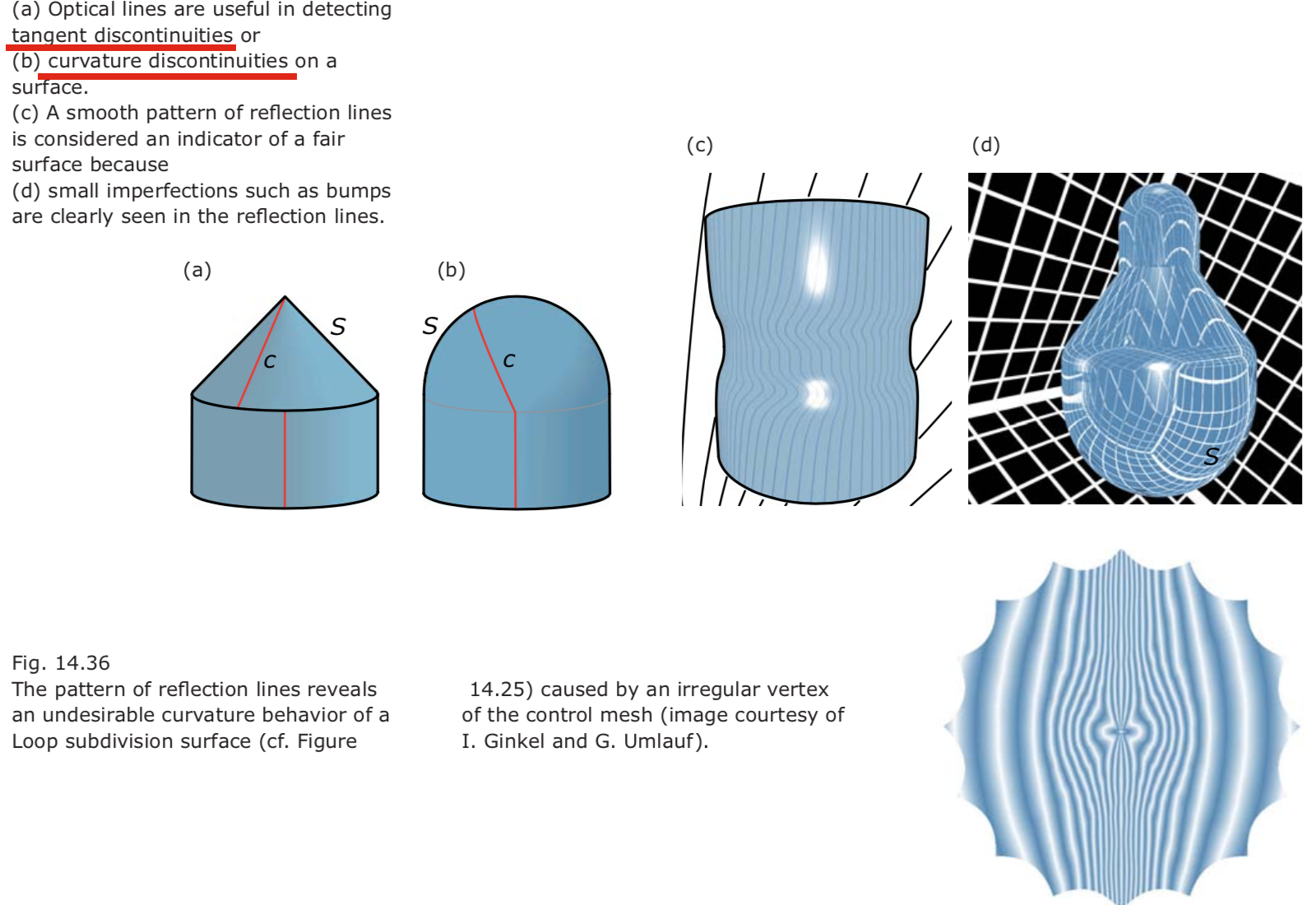
Optical lines for quality control 针对质量可控的光线

• A surface p(u,v) with continuous first derivatives leads to a reflection line that has continuous positions but may have tangent discontinuities.

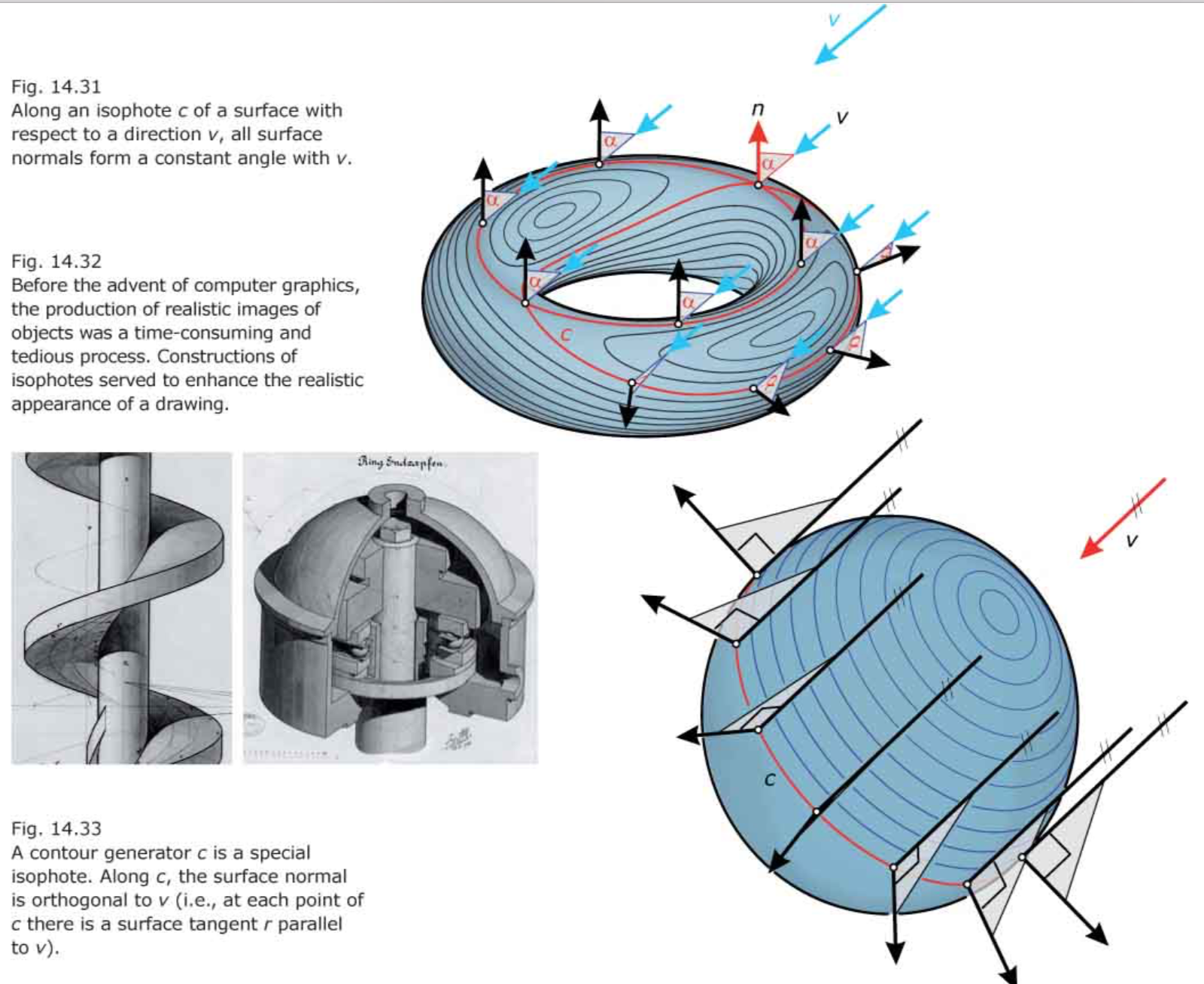
Isophotes 等照度

• These are isophotes, whose definition also depends on the surface normals.
• A curve c on S along which the surface normals form a constant angle α with v is called an isophote.

Contour generators

• At each point p of c, there is a line r parallel to v and normal to the surface normal (i.e., r is tangent to the surface).

Optical lines for shape analysis

• Surfaces con- structed with the subdivison algorithms of Doo-Sabin, Catmull-Clark or Loop are not curvature continuous at irregu- lar vertices of the input mesh.

In any case, we have to note that if we want to have smooth mirror images of smooth curves the mirror surface S must be curvature continuous. For a B-spline surface, this is achieved by using degree 3 or higher in both parameter directions.

Texture mapping 纹理映射

Digital elevation models 数字演化模型

• Placing an architectural design within its environmental context is useful and interesting for purposes of visualization and presentation, and can be essential for the actual construction
• two frequently used representations of topographic surfaces in digital elevation models: a grid-based approach and a triangulation.
• Assuming a smooth surface, the orthogonal network of level curves and curves of steepest descent is singular at critical points. These are defined as points with a horizontal tangent plane.

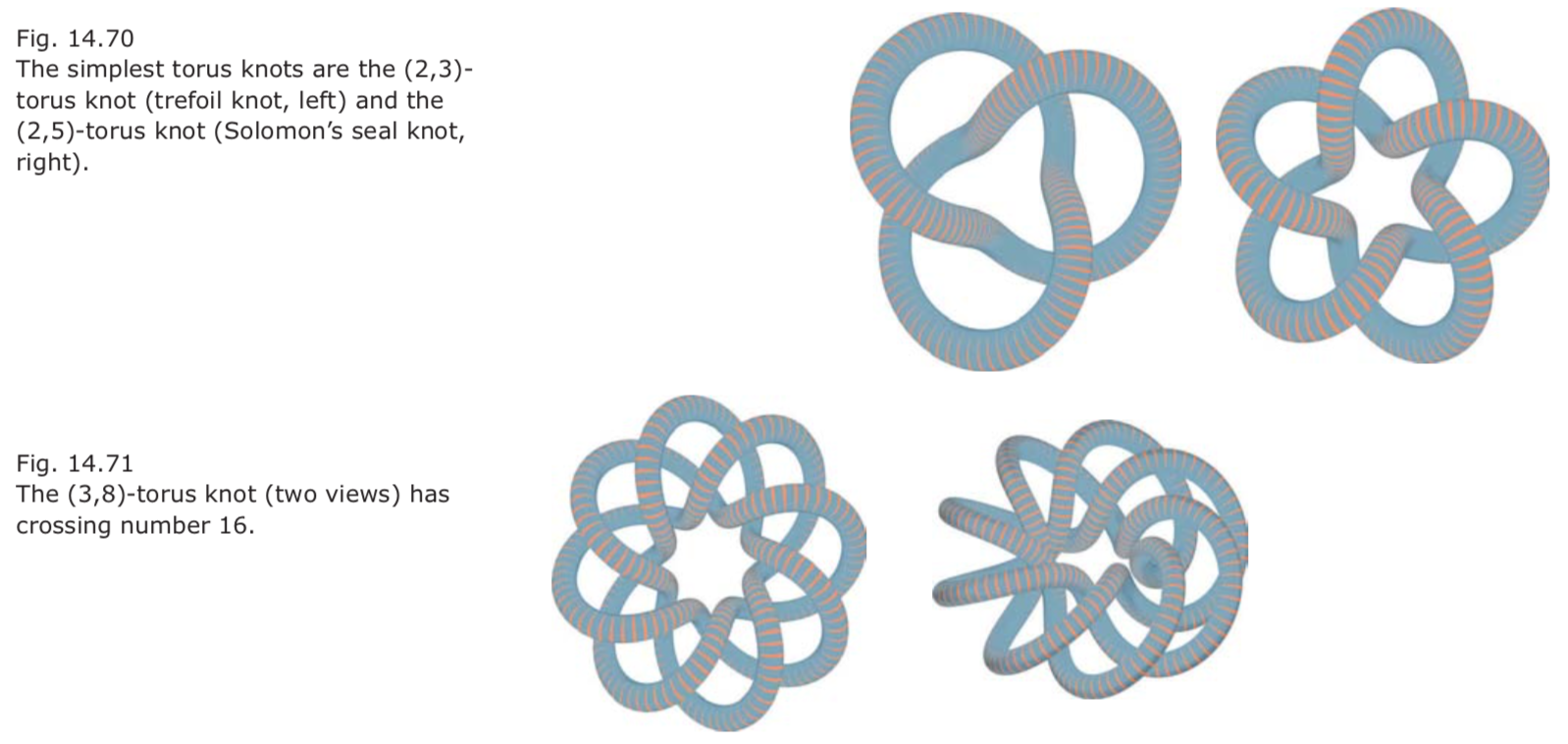
Geometric topology and knots 几何拓扑和扭结

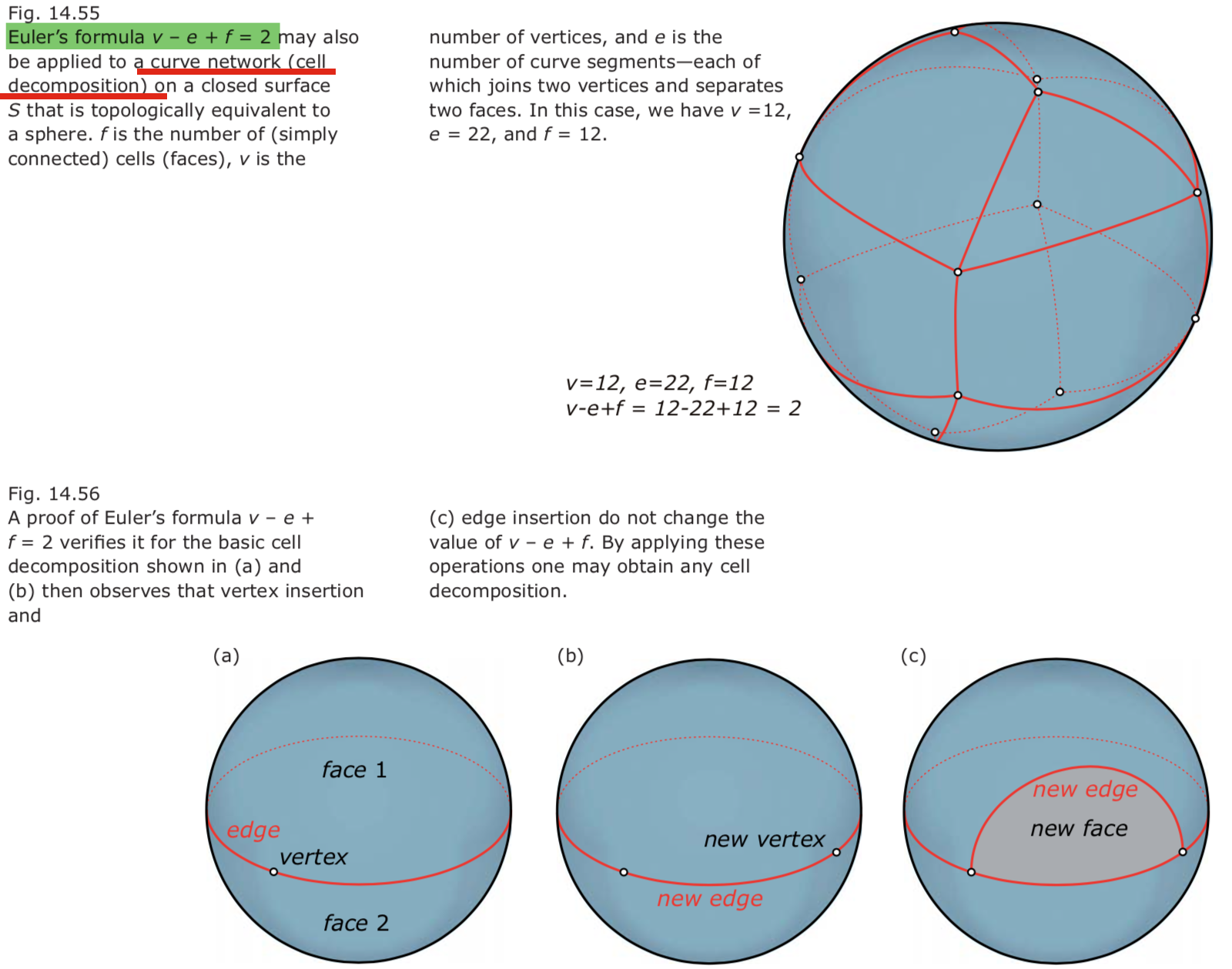
• If the polyhedron is topologically equivalent to a sphere, Euler’s formula holds: v – e + f = 2.
• the Euler characteristic for a surface topologically equivalent to a torus is zero: v – e + f = 0.
• χ = v–e+f = 1 for a Möbius band.

Classification of closed orientable surfaces

• any closed orientable surface S is equivalent to a sphere with a certain number g of handles. This number is called the topological genus of S. A sphere has genus g = 0, and a torus has genus g = 1. The Euler characteristic χ of a surface with genus g equals χ = v – e + f = 2 – 2g.