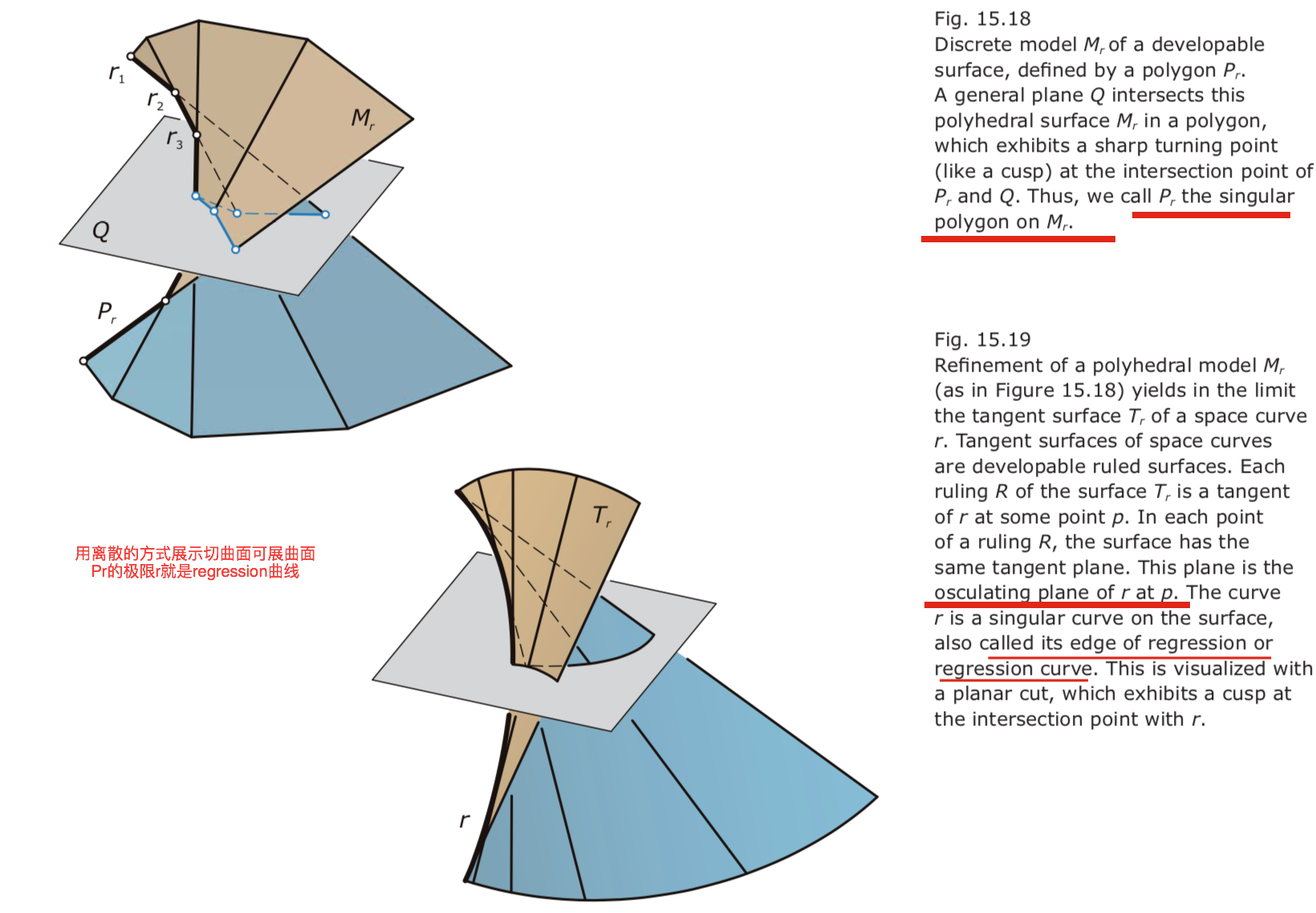
Developable surface and unfoldings

• Developable surfaces behave just like paper if we bend or twist them without tearing or stretching.

Surfaces that can be built from paper 能由纸张建造的曲面

• Developable surfaces S are characterized by the property that they can be mapped isometrically into the plane.
• Developable surface has the same Gaussian curvature as the plane (i.e., it has vanishing Gaussian curvature).
• Any ruling of such a developable ruled surface must be a torsal ruling R. This means that the surface S has the same tangent plane at all points of the same ruling R.
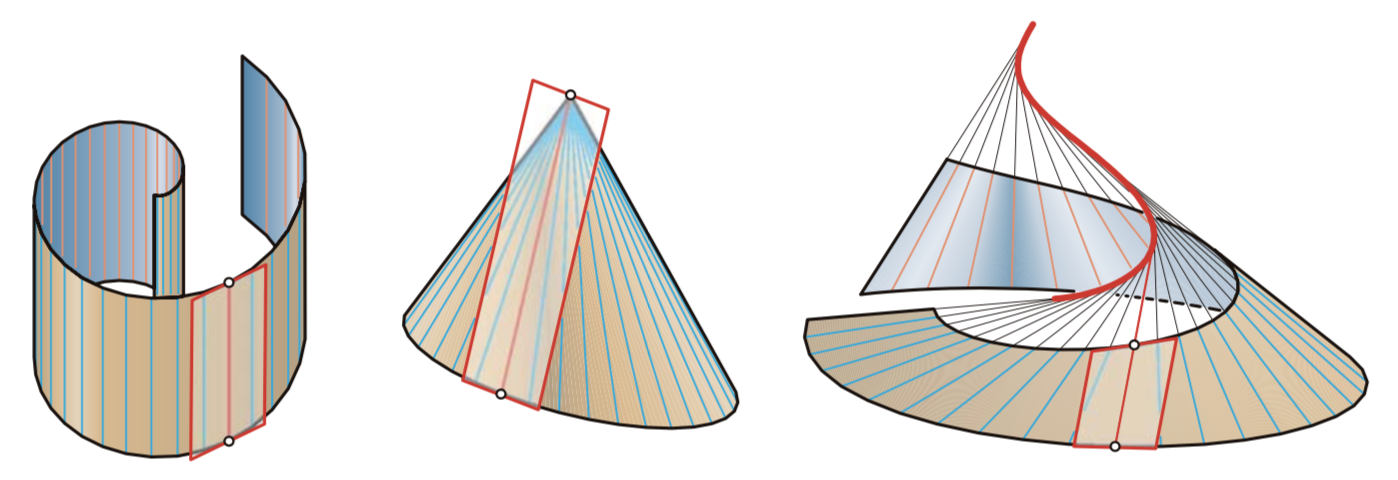
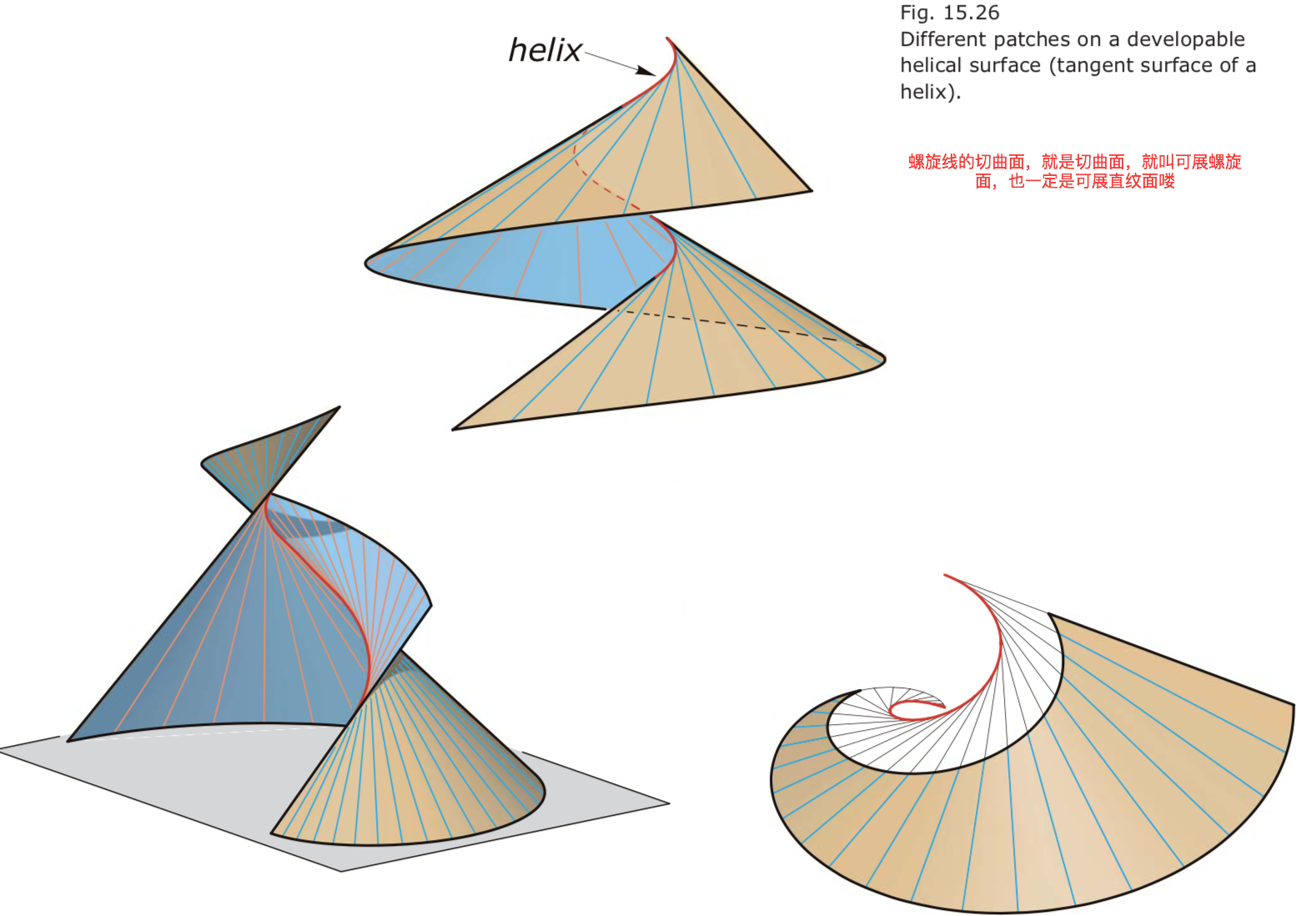
• Three basic types: cylinders, cones, and tangent surfaces of space curves.

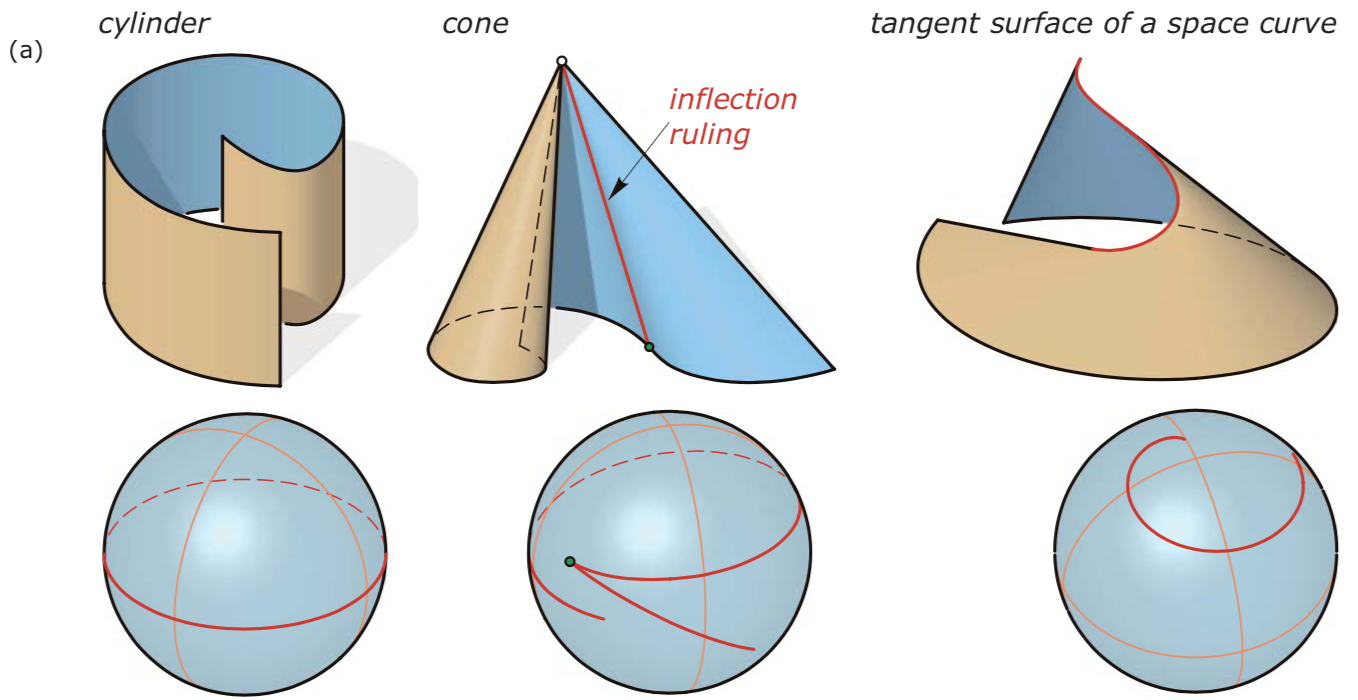
• cylinders, cones, tangent surfaces of space curves) have the following common properties: They are special ruled surfaces because a tangent plane is always tangent to the surface along an entire ruling and not just in a single point. We call such surfaces developable ruled surfaces.
• Moreover, the surfaces have vanishing Gaussian curvature because their spherical Gaussian image is just a curve. Therefore, a developable surface contains only parabolic surface points or flat points.
• Thus, the offset surface Sd is also a developable surface.
• The offset surfaces of a cone are in general not cones!
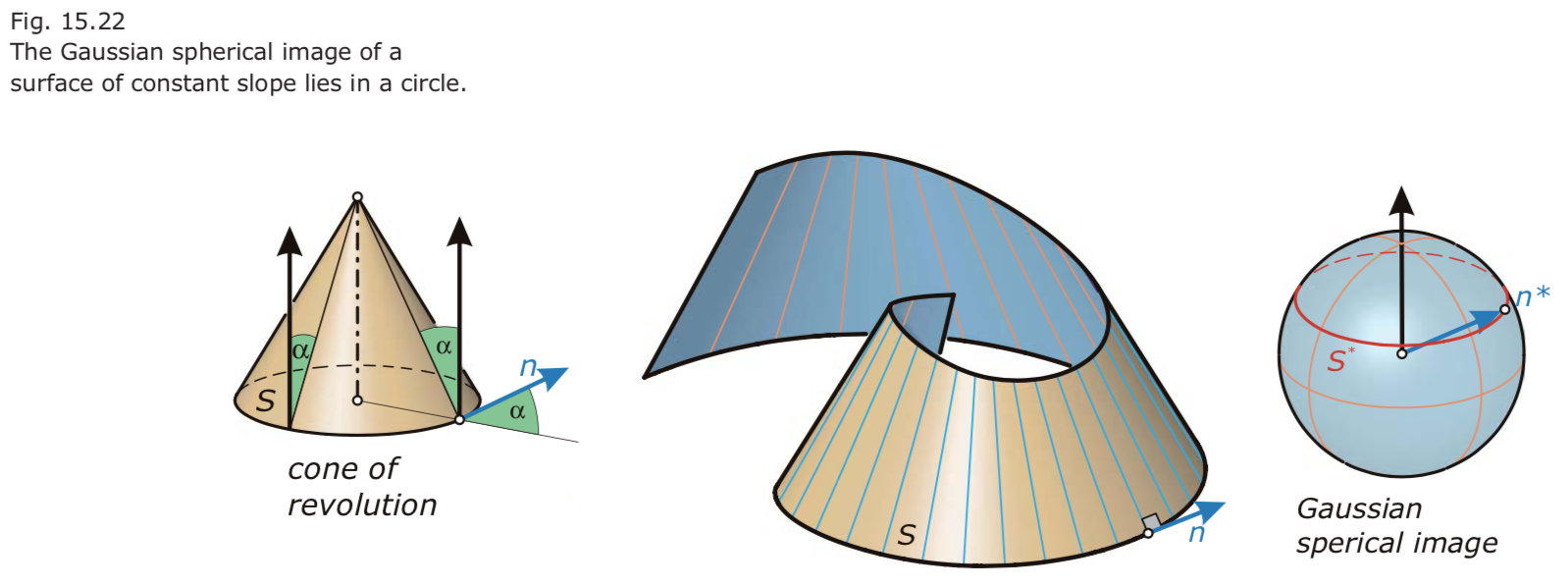
• Surfaces of constant slope are developable.

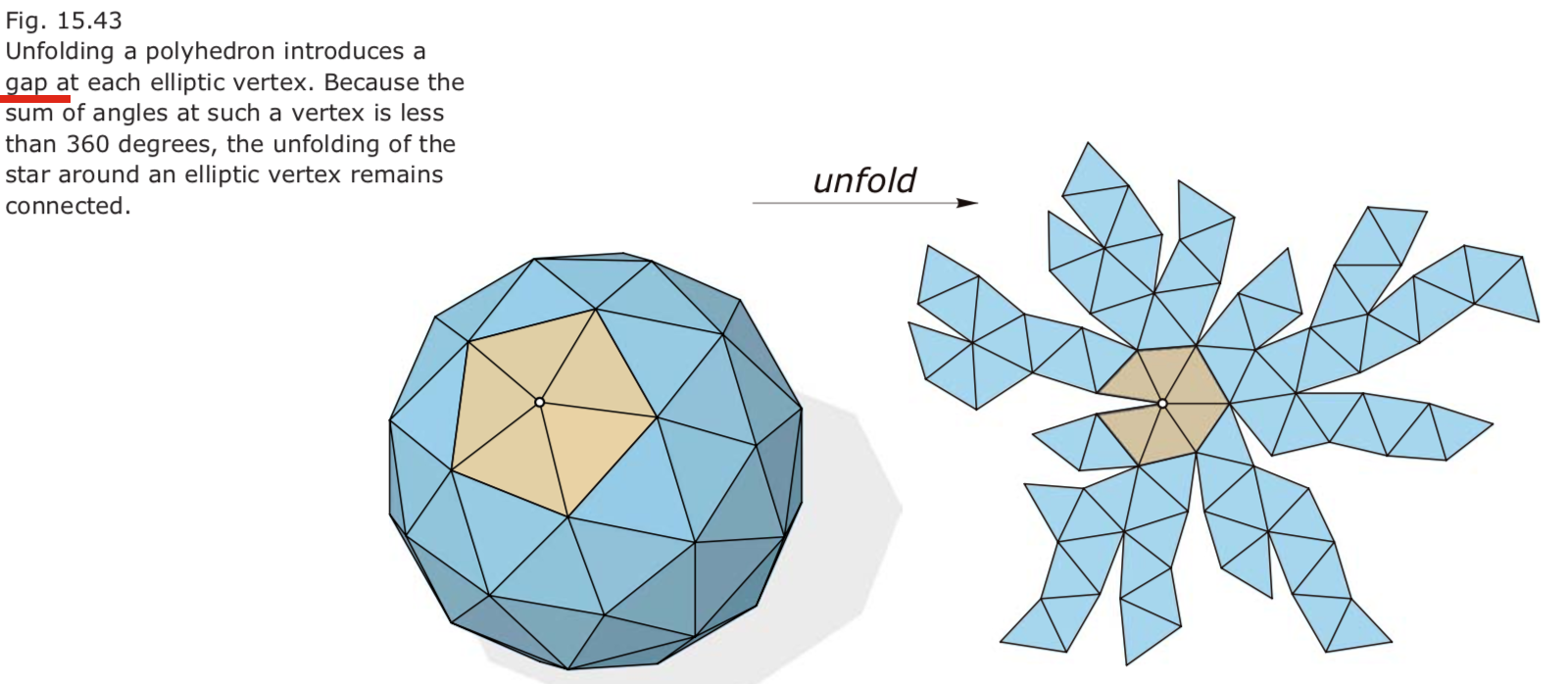
Unfolding a polyhedron 展开多面体