Shape optimization problems

• The realization of a design idea in an optimal way, both from the aesthetic and functional perspective, is a difficult and complex problem area.

Remarks on mathematical optimization 数学优化注解

• Any optimum is only an optimum within the conceptualization of the problem space and the boundary conditions applied.
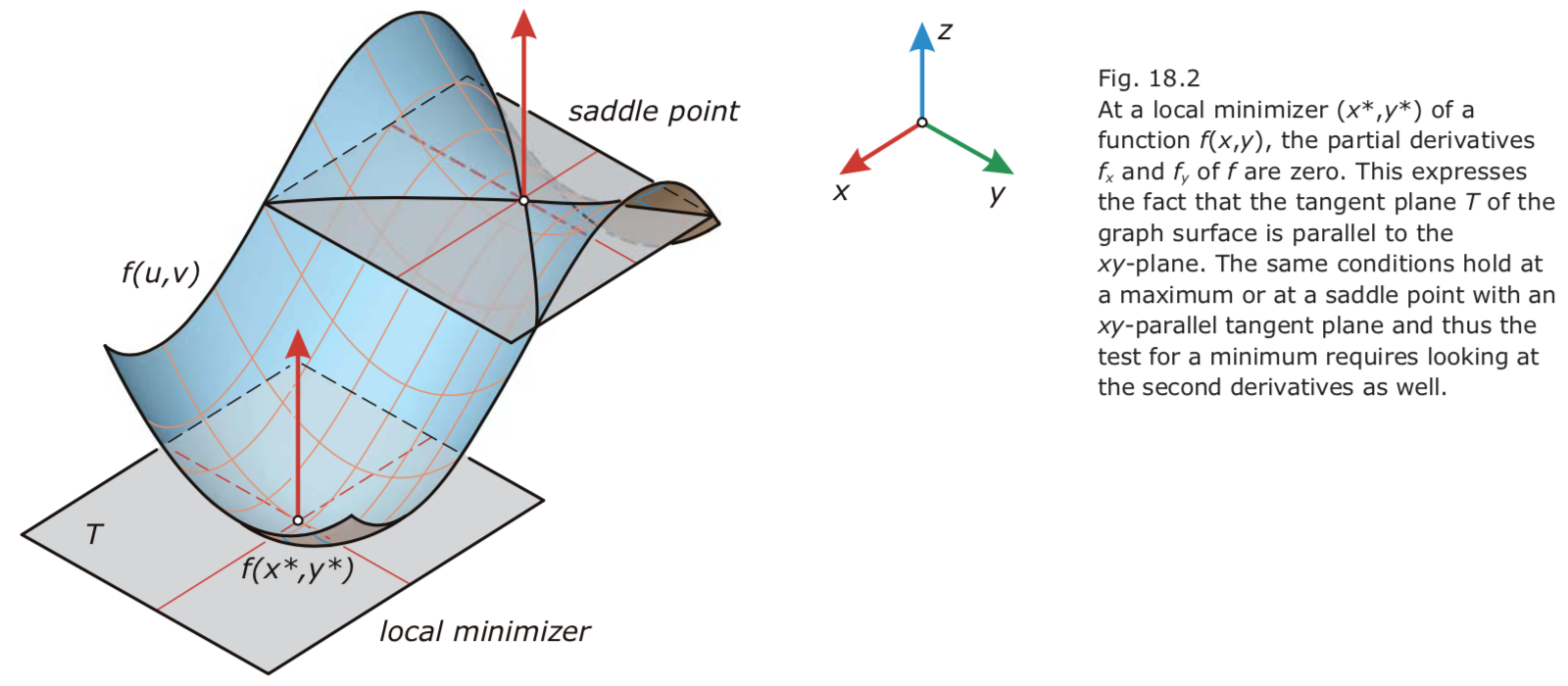
• Gradient descent.
  We form the gradient ∇f = (fx ,fy), which is the vector whose coordinates are the partial derivatives of f with respect to x and y.
  To move “downhill” toward a minimum one may always move in the direction of the negative gradient –∇f.

Geometric optimization 几何优化

• Minimal surfaces
  Given a smooth closed curve c without self-intersections, find the surface patch with boundary curve c that has the smallest surface area A.

• A minimal surface has vanishing mean curvature in each of its points. 极小曲面的平均曲率为0
• a generic surface point p of a minimal surface must be a hyperbolic point (saddle-like) 极小曲面点是双曲点
• This is a hyperbolic paraboloid whose rulings in the plane z = 0 are the two orthogonal straight lines x + y = 0 and x – y = 0. These straight lines are the asymptotic directions (directions of vanishing normal curvature). 平面z=0与双曲抛物面相交的是两条正交直线rulings，是渐近线
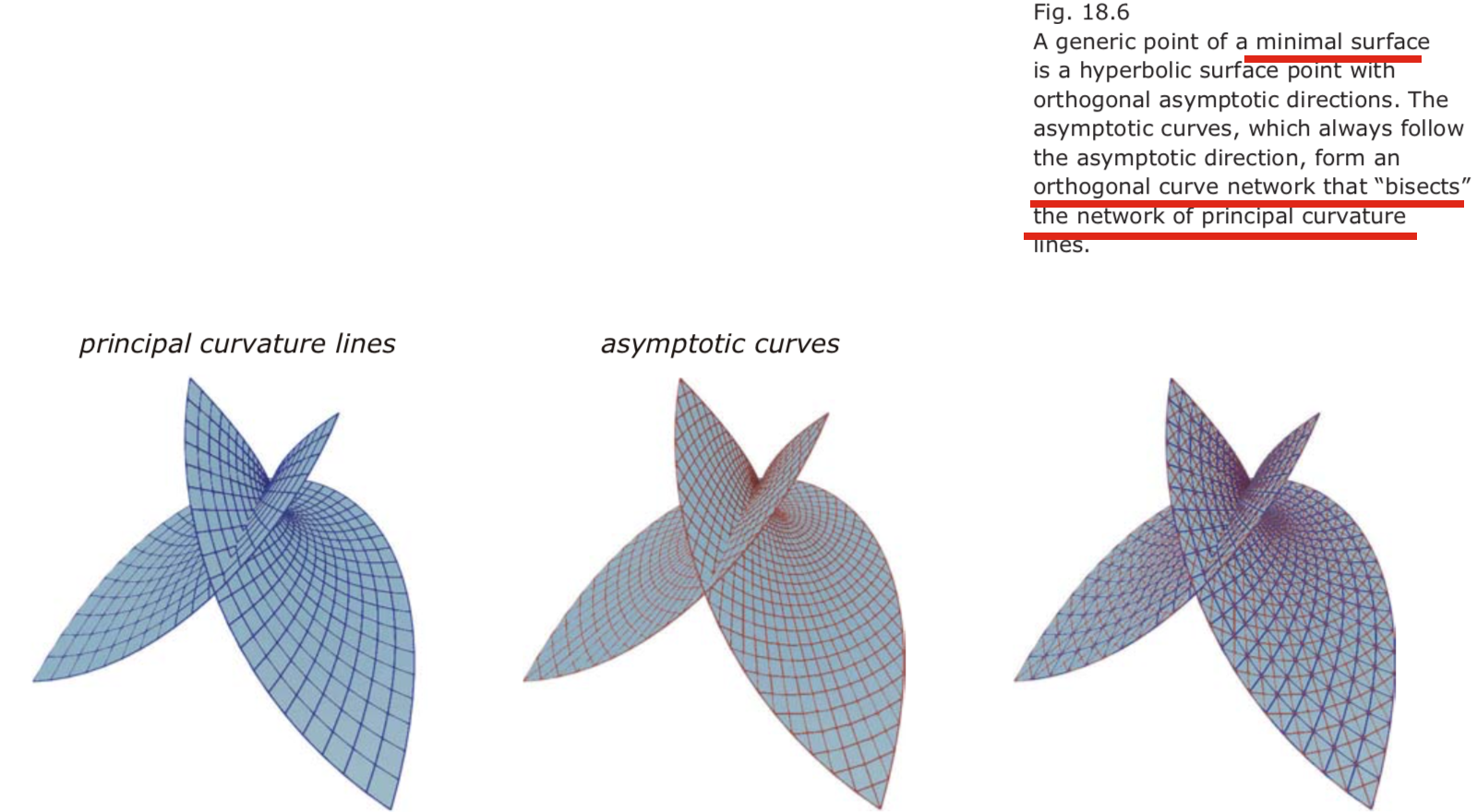
• in each point of a minimal surface the asymptotic directions are orthogonal. 极小曲面的每个点，渐近方向正交
• the bisecting lines of the (always orthogonal) principal directions are the asymptotic directions. 主法曲率线的对角线是渐近方向
• on a minimal surface the asymptotic curves form an orthogonal curve network. It is the bisecting curve network of the network of principal curvature lines. 极小曲面，渐近线网是正交网，也是对分正交的主法曲率网得到的
• For a minimal surface, the asymptotic curve network is also mapped to an orthogonal curve network of S. This is a result of the remarkable property that the Gaussian spherical mapping of a minimal surface S to the unit sphere S is conformal (angle preserving). 极小曲面的高斯球像是共形映射（保角），因此正交的渐近网的高斯像也是正交的

enneper 曲面、 helicoid曲面、catenoid曲面、Scherk极小曲面

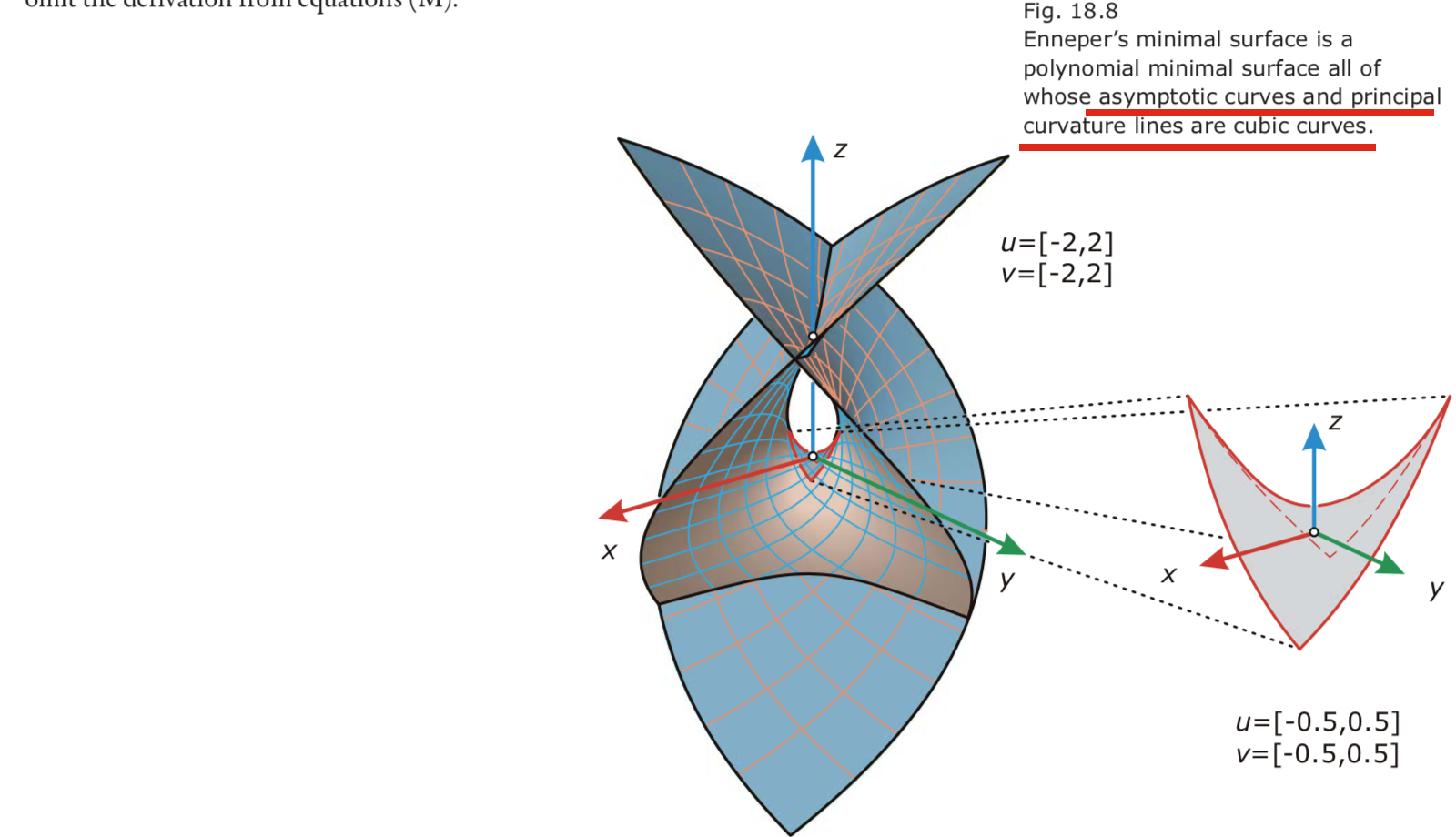
• Enneper.
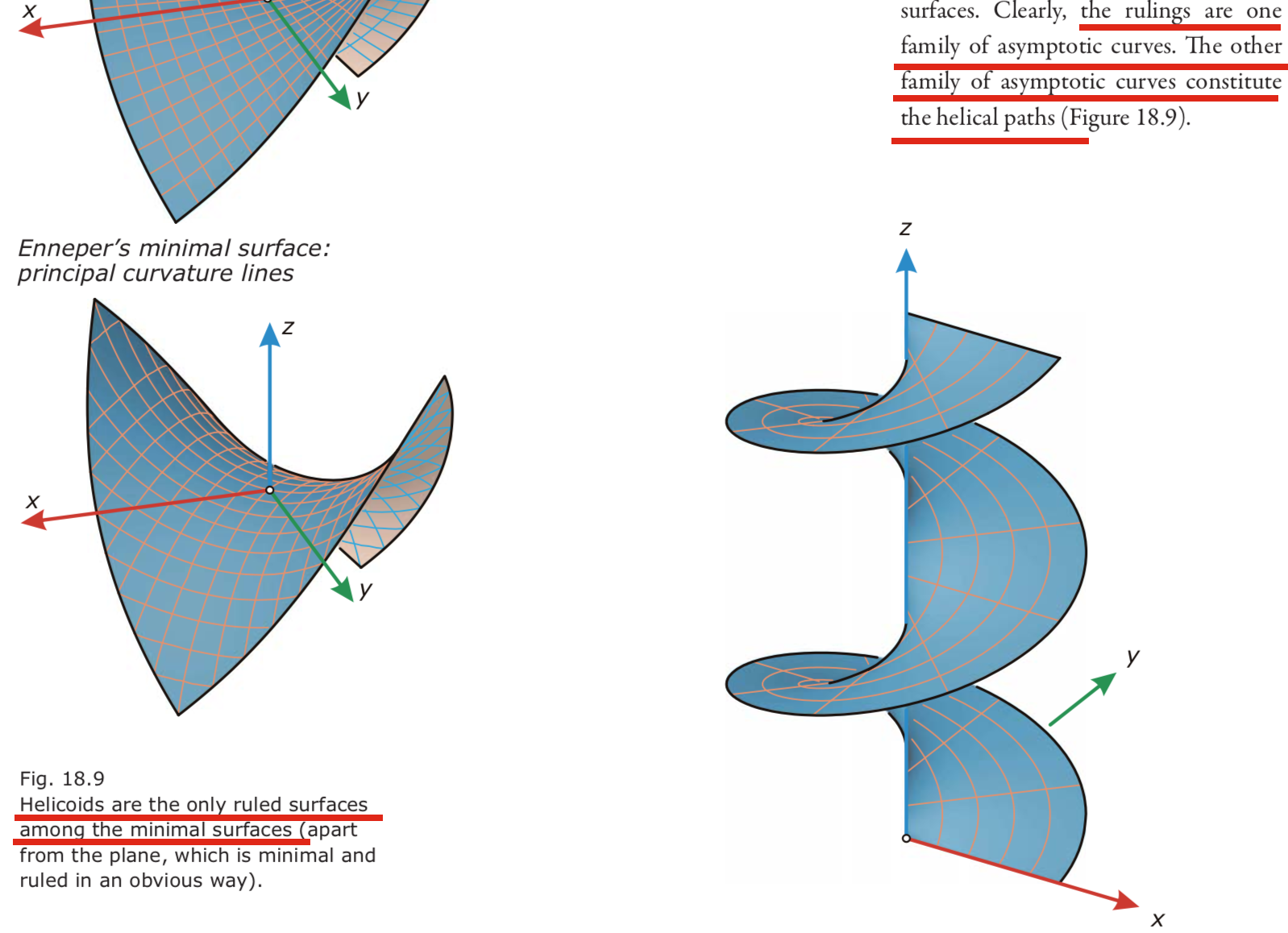
• Helicoid. 唯一的直纹极小曲面
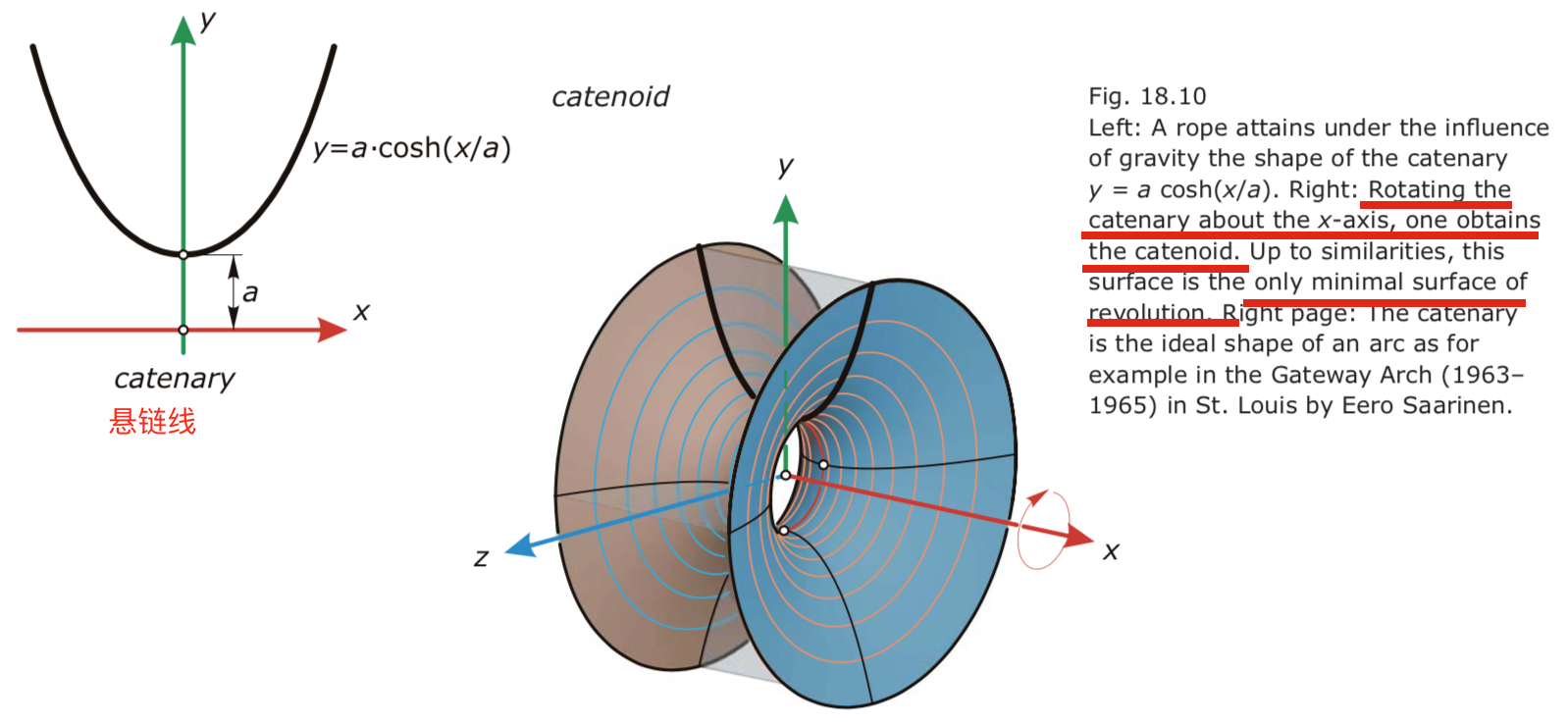
• Catenoid. 悬链面：唯一的旋转极小曲面
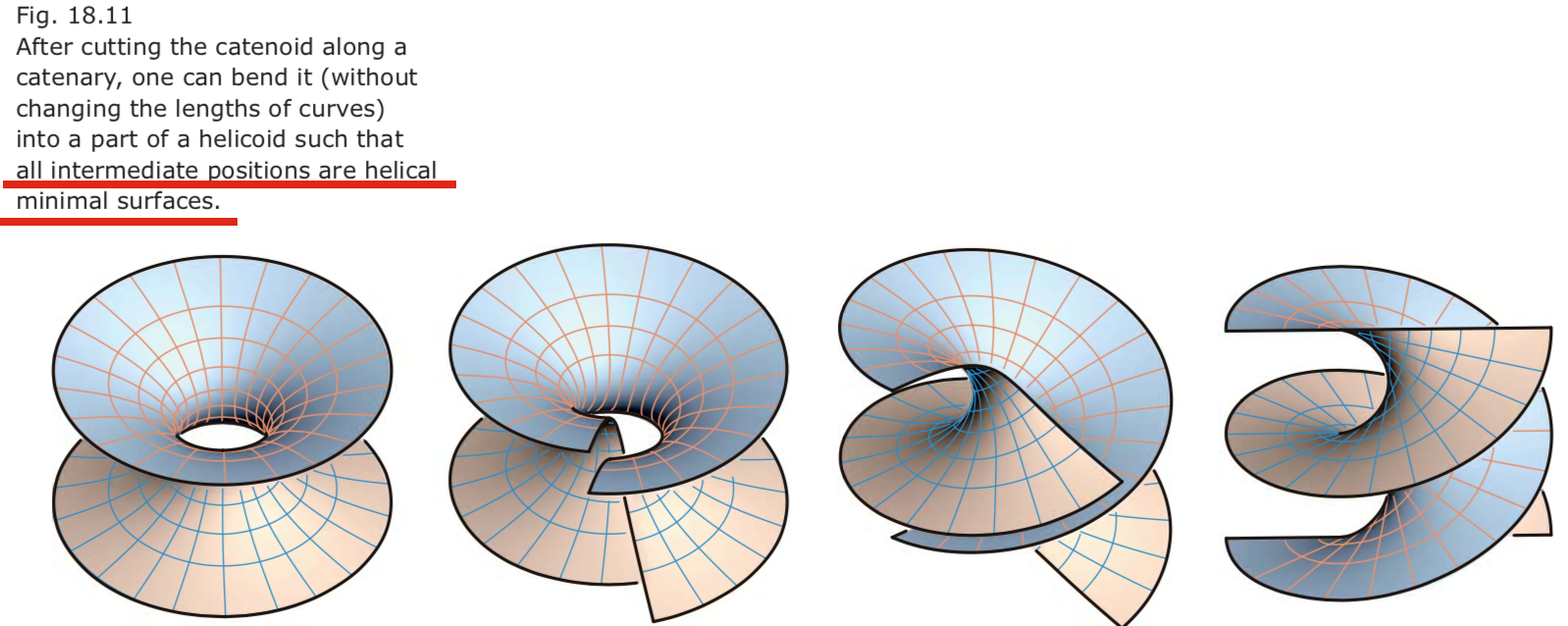
• Helical minimal surface. 由catenoid剪开变化得到，每个过程都是极小曲面
• Scherk’s minimal surface.

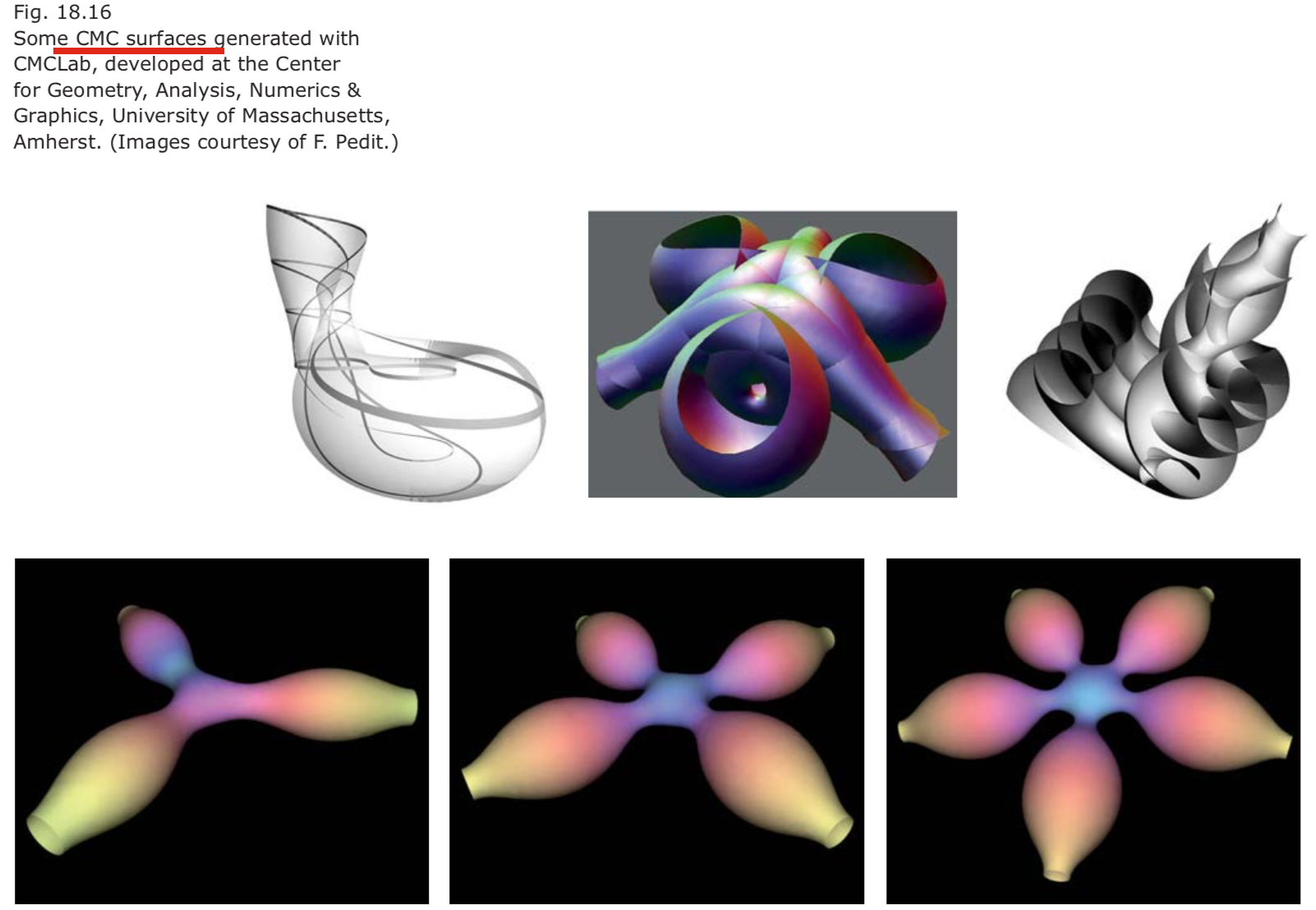
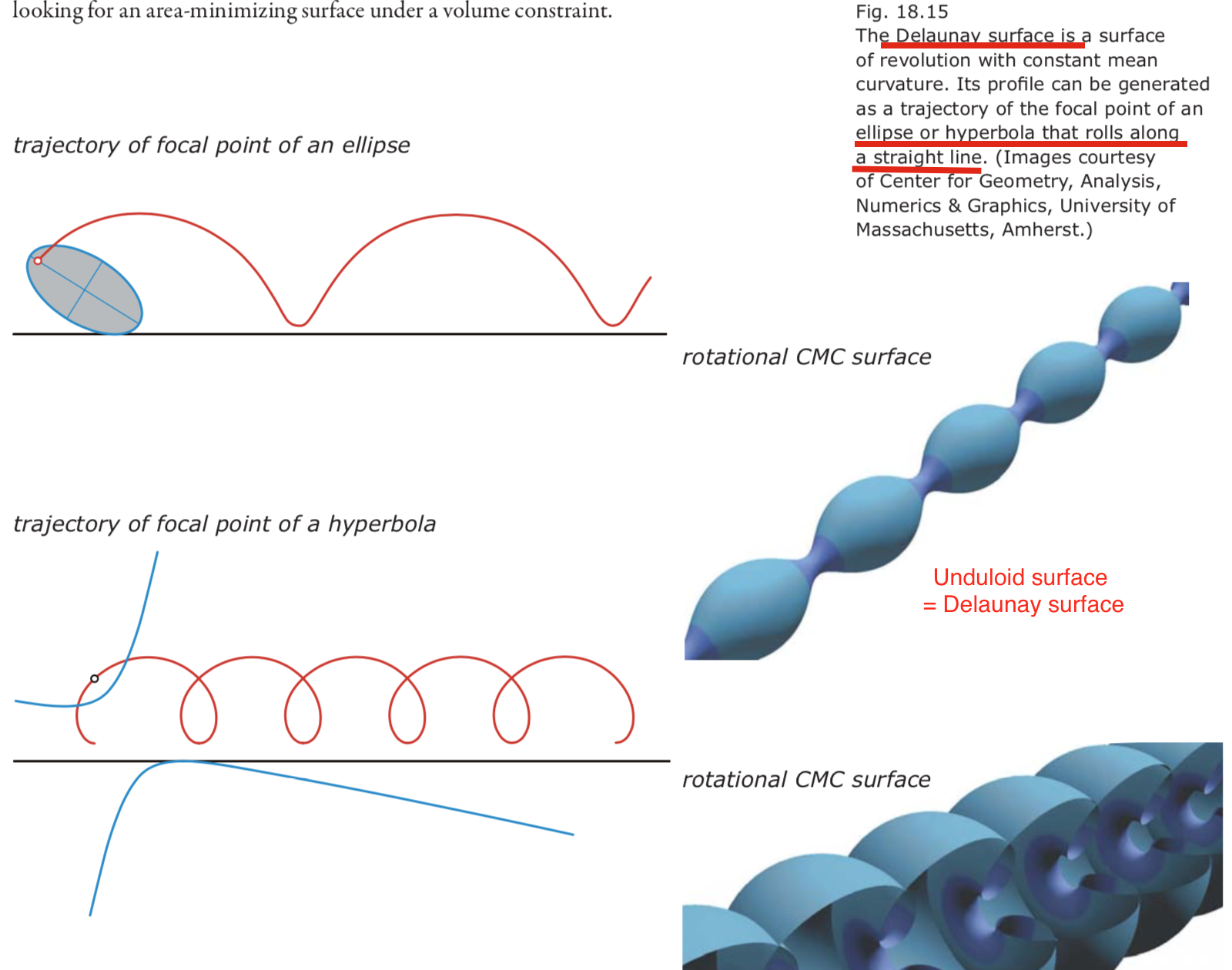
• Surfaces with constant mean curvature

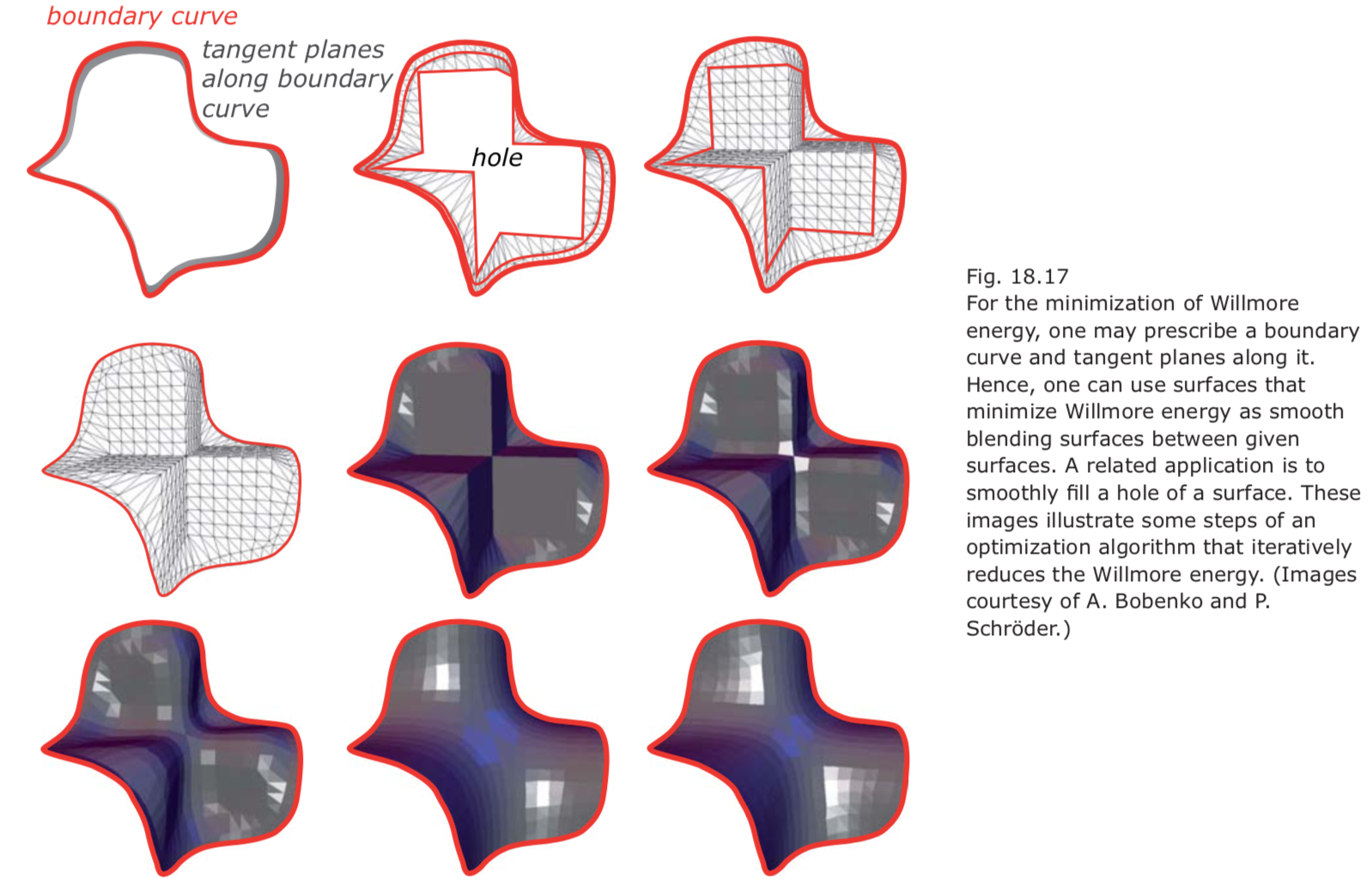
• Willmore energy.
  Willmore energy is the surface integral of the function $(k_1 – k_2)^2$: \(E_W = ∫S(k_1 – k_2)^2dA.\)
• Willmore energy tries to make surfaces as spherical as possible.
• An important advantage of the Willmore energy is that one can prescribe a boundary strip (i.e., a boundary curve plus tangent planes along it) and compute an energy minimizer that interpolates these data.

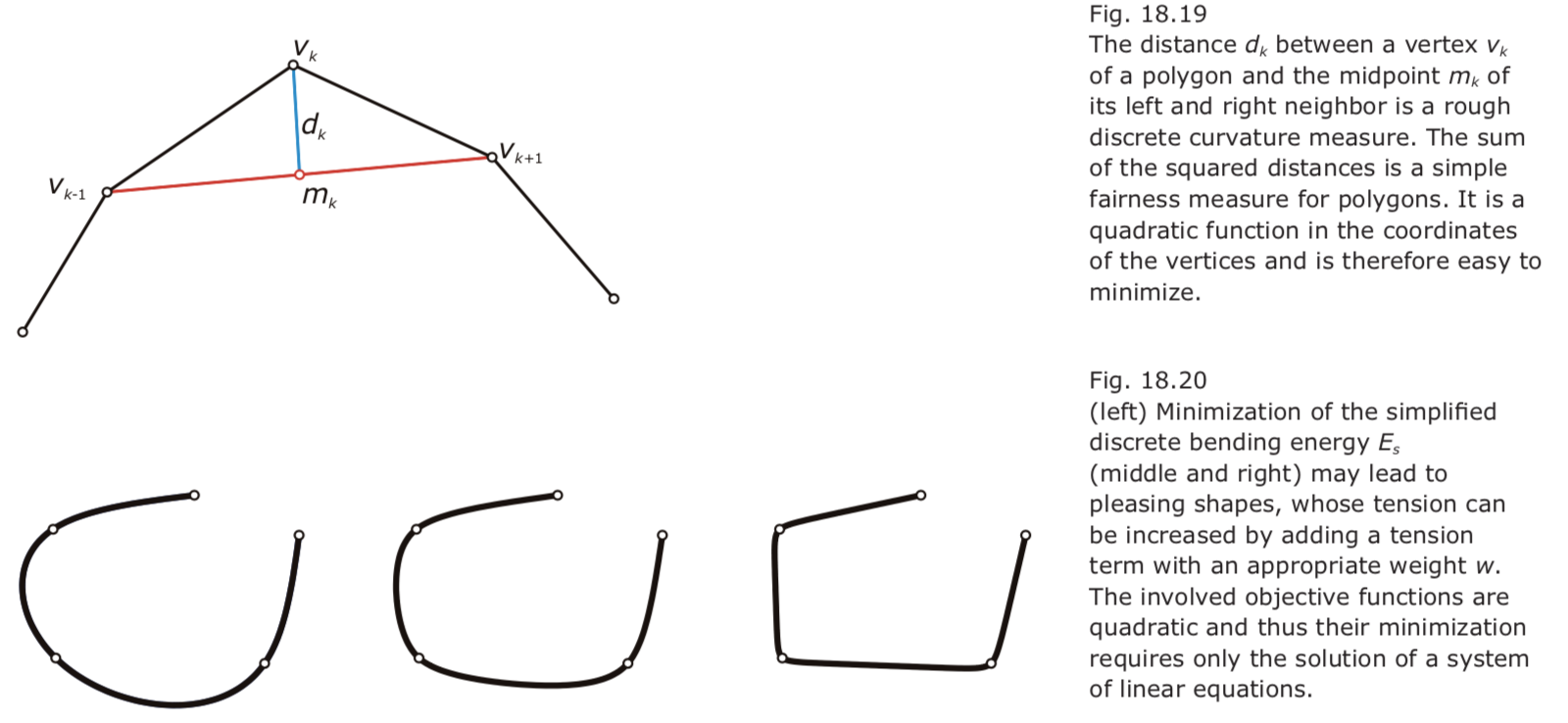
• Fair curves and polygons.
  The bending energy of an idealized thin elastic beam is proportional to the integral of the squared curvature, expressed as $E=∫c k^2 ds.$ 用$Es = (1/4) ∑(v_{k-1} + v_{k+1} – 2v_k)^2$替代求解.

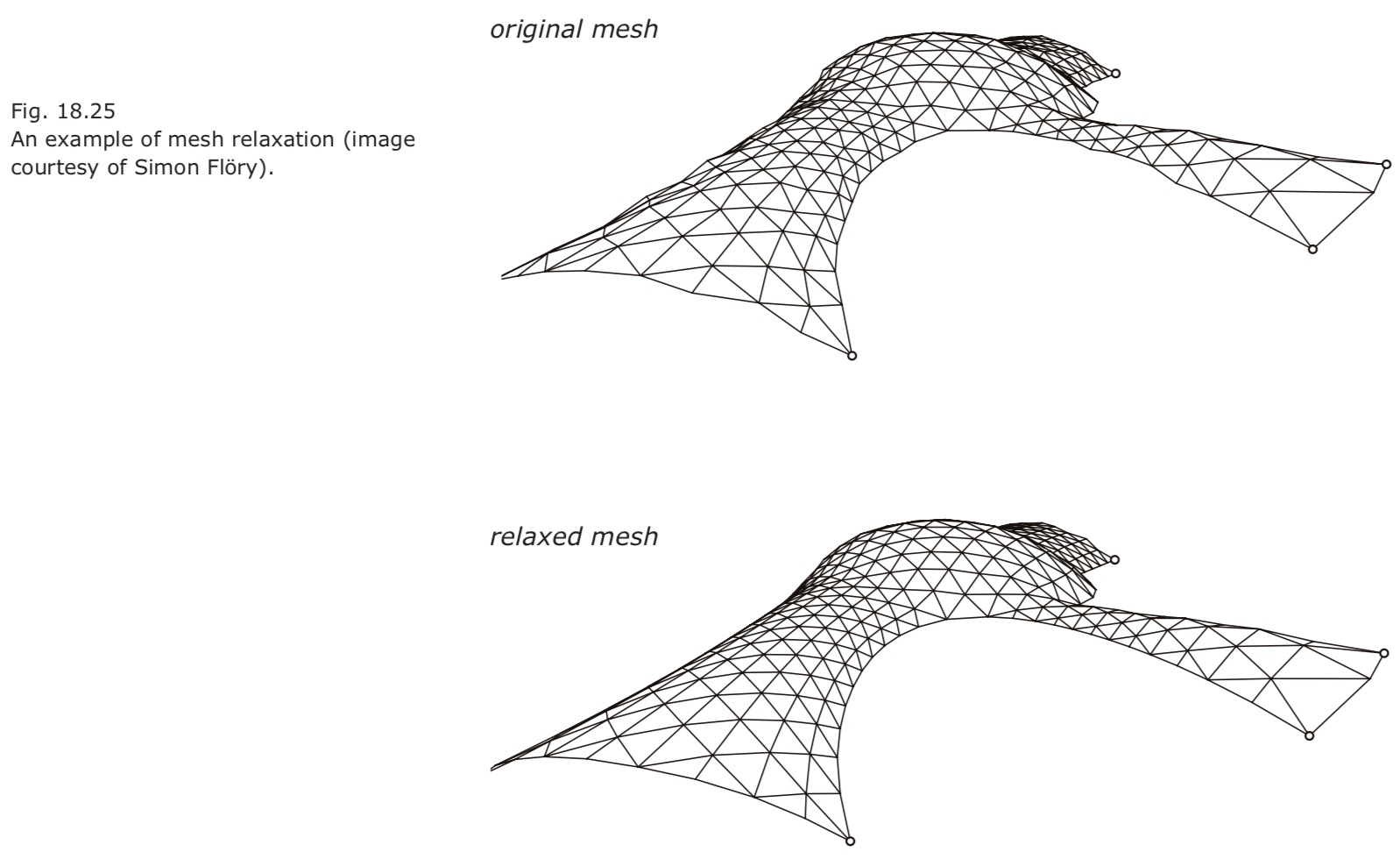
• Fair webs and mesh beautification.
• Geometric constraints.

Functional optimization 函数优化

References and further reading